钢结构的设计采用以概率理论为基础的极限状态设计法,用分项系数的设计表达式进行计算,承重钢结构或构件应按承载能力极限状态进行设计。
1.结构功能函数
设决定结构可靠性(或安全性)的参数有n个:x1,x2,…,xn。构件为符合某一功能规定要求(如应力不超过材料强度或变形不超过规定的限值等),依据设计准则可以建立起包含这n个参数的函数关系式,即
Z=g(x1,x2,…,xn) (1-1)
式(1-1)称为结构功能函数。
为说明概念,设功能函数中只包含结构(或构件)抗力R与荷载效应S这两个基本随机变量,所以可将式(1-1)简化为
Z=g(R,S)=R-S (1-2)
在式(1-2)中,因为R和S是随机变量,所以函数也是随机变量。在实际工程中,R和S的实际取值均存在着不确定性,具有一定的概率分布。因此随机变量Z的取值可能大于0、等于0或小于0,这三种情况分别代表结构功能所处的不同状态:
当Z<0时,结构功能处于失效状态;
当Z=0时,结构功能处于临界状态;
当Z>0时,结构功能处于可靠状态。
2.结构功能极限状态
为了确保结构的安全性和正常使用,设计规范规定结构或构件在不同的情况下要有效地完成特定功能,并且规定一个特定临界状态指标,当结构或构件超过所规定的特定临界状态指标时,即可认为结构功能失效。由此所确定的结构功能临界状态就叫作结构或构件的功能极限状态。设计规范规定了结构或构件的多种特定功能,因此结构功能极限状态可分为以下两类。
1)承载能力极限状态。承载能力极限状态主要指的是结构或构件达到最大承载能力或出现不再符合继续加载的变形。承载能力极限状态破坏包括倾覆、强度破坏、丧失稳定、疲劳破坏、结构变为机动体系或出现过度的塑性变形。
2)正常使用极限状态。正常使用极限状态主要指的是结构或构件达到正常使用或耐久性能的某项规定限值。而正常使用极限状态破坏则包括出现影响正常使用的振动,出现影响正常使用或耐久性能的局部损坏,以及出现影响正常使用或影响外观的变形。
3.结构可靠度
按照概率极限状态设计方法,结构的可靠度是指结构在规定的时间内以及规定的条件下,完成预定功能的概率,即Z≥0的概率。
结构可靠度的数学表达式为
Ps=P(Z≥0) (1-3)
结构失效概率的数学表达式为
Pf=P(Z<0) (1-4)
事件(Z<0)与事件(Z≥0)是功能函数取值完整空间,且二者相互独立。因此有
Ps+Pf=P(Z≥0)+P(Z<0)=1 (1-5)
由式(1-5)得
Ps=1-Pf (1-6)
式(1-6)说明,结构可靠度的计算可通过利用间接计算结构失效概率来获得。
若已知功能函数Z的概率密度fZ(Z)曲线(图1-10),则结构失效概率Pf(图1-10的阴影部分)可以由下面积分求得,即
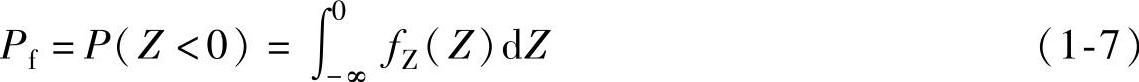
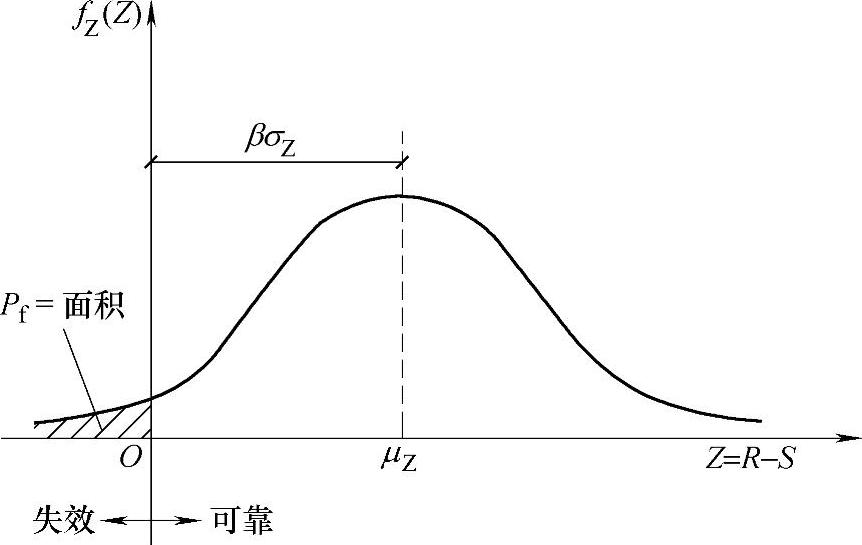
图1-10 Z的概率密度fZ(Z)曲线
但实际上,Z的分布通常很难求出,由式(1-7)计算失效概率的方法也仅是停留在理论上。20世纪60年代末,美国学者康奈尔(C.A.Cornell)提出了一次二阶矩方法,概率设计法在实际中得到应用。
一次二阶矩法不是由图中Z的分布直接计算结构的失效概率Pf,而是把功能函数Z的均值μZ用Z的标准差σZ来度量,即
μZ=βσZ (1-8)
由上式可得

式中 β——结构的可靠度指标或安全指标。
显然,只要确定了分布,β与Pf就会存在一一对应关系。若Z为正态分布,则β与Pf的关系式为
Pf=ϕ(-β) (1-10)
式中 ϕ(·)——标准正态分布函数。
若Z为非正态分布,则可用当量正态化方法将其转化为正态分布。
由式(1-10)可知:若β增大,则Pf减小;反之亦然。Z为正态分布,β与Pf的对应关系见表1-1。
表1-1 Z为正态分布时β与Pf的对应值

对于任何分布Z的σ2Z和μZ均可根据下式求得,即(https://www.xing528.com)
μZ=μR-μS (1-11)
对于R与S统计独立情况,有
σ2Z=σ2R+σ2S (1-12)
式中 μR、μS——抗力R和荷载效应S的均值;
σ2R、σ2S——抗力R和荷载效应S的方差。
若Z为设计参数的非线性函数,则应展开为泰勒级数并取其线性项,然后再进行计算其均值和方差。
μZ≈g(μx1,μx2,…μxn) (1-13)

式中 μxi——随机变量xi的均值;
(·μ)——计算偏导数时变量均用各自的均值赋值。
4.设计表达式
(1)承载能力极限状态表达式 对于承载能力极限状态设计,应该采用荷载效应的基本组合或偶然组合。
1)荷载效应的基本组合应根据组合式的最不利值来确定。
可变荷载效应控制的组合为
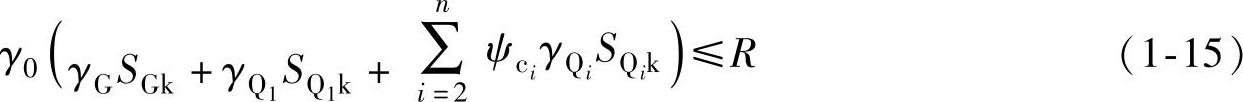
永久荷载效应控制的组合为
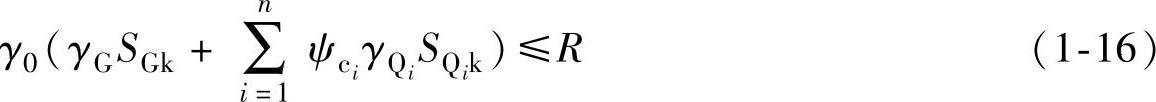
式中 R——结构构件抗力的设计值,R=Rk/γR。其中Rk是抗力的标准值,取其概率分布的0.05下分位点,rR是抗力分项系数;
γ0——结构重要性系数;
SGk——按照永久荷载标准值计算的荷载效应值(如构件或连接中的应力);
SQik——按照第i个可变荷载标准值计算的荷载效应值;
SQ1k——所有可变荷载效应值中起控制作用的值(将该值放在特殊位置计算,使计算结果最大);
γG——永久荷载分项系数;
γQi——第i个可变荷载分项系数;
γQ1——起控制作用的可变荷载分项系数;
ψci——第i个可变荷载的组合系数,ψci≤1。
对于一般排架、框架结构,可以采用简化规则。由永久荷载效应控制的组合,仍根据式(1-16)进行计算。当只有一个可变荷载时,由可变效应控制的组合为
γ0(γGSGk+γQ1SQik)≤R (1-17)
若有多个可变荷载时,则由可变效应控制的组合为
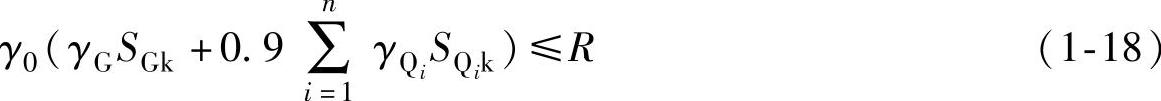
2)对于偶然组合,荷载效应组合的设计值宜按照以下规定确定:偶然荷载的代表值不乘以分项系数;与偶然荷载同时出现的其他荷载可依据观测资料和工程经验采用适当的代表值。各种情况下荷载效应的设计公式可根据相关规定确定。
(2)正常使用极限状态表达式 当验算变形是否超过规定限值时,用荷载的标准值计算,不考虑荷载的分项系数。荷载效应的组合有短期组合(标准组合)与长期组合(准永久组合)。钢结构或构件只按短期组合,其表达式为
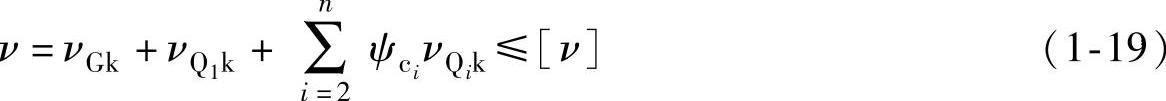
式中 ν——结构或构件的变形值;
νGk——按照永久荷载标准值计算的结构或构件的变形值;
νQik——按照第i个可变荷载标准值计算的结构或构件的变形值;
νQ1k——由可变荷载标准值计算的结构或构件的变形值中起控制作用的值;
ψci——第i个可变荷载的组合系数,当有风荷载参与组合时取0.6,无风荷载时取
1.0;一般框、排架,当有两个或两个以上荷载参与组合且有风荷载时取0.85,其他情况取1.0;
[ν]——结构或构件的容许变形值。
当只有一个可变荷载时,有
ν=νGk+νQ1k≤[ν] (1-20)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




