有源RC滤波器的原理与应用

一、 概述

1.什么是滤波器

在上一节介绍的动态电阻应变仪和谐振鉴频器中，π形LC回路和RC回路可以将缓变的调制信号从高频的载波中分离出来，这些电路起的作用称为滤波作用。在机械设备中，经常采用各种隔振、防噪声的装置，这些装置起的作用也是滤波作用。各类仪器、仪表都有一定的工作频率范围，这说明它们本身都有滤波作用。广义地讲，凡是可以使信号中特定的频率成分通过，而极大地衰减或抑制其他频率成分的装置或系统都称之为滤波器。

图5-25表示一滤波器系统，系统的脉冲响应函数为h（t），频率响应函数为H（jω）。设输入信号为x（t），输出信号为y（t），则输出、输入与滤波器系统特性在时域和频域中的关系分别为

图5-25 滤波器系统

y（t）＝x（t）*h（t）　（5-19）

Y（jω）＝X（jω）H（jω）　（5-20）

可见，只要改变滤波器的特性，在输入信号不变时，就可以得到不同的输出，即会产生不同的滤波效果。

2.滤波器的类型

根据滤波器本身的特性、组成元件以及在实际使用时对滤波器的结构形式和性能要求不同，滤波器可以有不同的分类。

（1）根据频率特性不同，滤波器分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器四类，它们的理想幅频特性图如图5-26中的（a）～（d）所示。滤波器中能使信号通过的频带称为通带，信号不能通过的频带称为阻带。

图5-26 四类滤波器的幅频特性

低通滤波器用上截止频率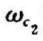描述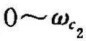，内的信号可以不受衰减地通过；高通滤波器用下截止频率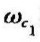描述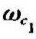，～∞内的信号不受抑制。带通滤波器的通带为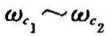，通带在频域上的位置可以用上、下截止频率的几何平均值，即中心频率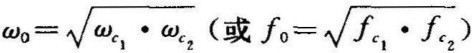来表示，通带宽记为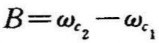（或B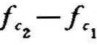＝）。与带通滤波器相反，带阻滤波器是专门用来抑制某一频段的信号，其阻带宽B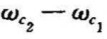＝，阻带在频域上的位置也用其中心频率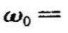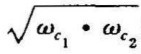来表示。

由幅频特性图可知，低通滤波器与高通滤波器，带通滤波器与带阻滤波器呈一种互补关系；带通、带阻滤波器也可由低通和高通滤波器串、并联得到。因此，高通、带通和带阻滤波器的频率特性，都可以用频率变换的方法从低通滤波器的频率特性中推导出来。

（2）滤波器还有其他不同的分类方法。根据滤波器的物理原理，可分为机械式滤波器和电路式滤波器。在非电量测试过程中，由于信号多转换成电压或电流形式，因此电测法中常采用由电子元件组成的网络做滤波器。根据构成滤波器的元件类型，可分为RC、LC和晶体谐振滤波器。在电路中含有有源器件（如运算放大器）的滤波电路称为有源滤波器；不含有有源器件的称为无源滤波器。由于集成电路的发展和有源滤波器所具有的独特优点，现在有源滤波器已成为滤波器的主要应用形式。此外，根据滤波器处理信号的形式，滤波器分为处理连续信号的模拟滤波器和处理离散信号的数字滤波器。随着数字计算技术和计算机在工程测试中的广泛应用，数字滤波方法用得越来越普遍。

3.滤波器的作用

滤波器是现代测试系统中的一个重要环节，滤波器的选频特性在测试过程中、在信号的传输和分析中有着重要的作用。

滤波器可以将有用的信号与大量的干扰噪声分离开来，这样，可以提高信号传输过程中的抗干扰性，提高信噪比。由于在测试过程中干扰信号总是与被测信号并存的，因此信号检测与处理过程中一个重要的内容是解决滤波问题。滤波器还可以用来滤掉被测信号中不感兴趣的频率成分。如用低通滤波器滤掉调制波中的高频成分，从而得到低频的调制信号；在数字信号分析系统中，输入的模拟信号要进行抗频混滤波处理，即将不感兴趣的高频成分滤掉，这样，一方面可以提高分析精度，另一方面可以降低对分析仪器的性能要求。滤波器的另一种重要用途是对动态信号进行频谱分析，即通过分辨力高的窄带滤波器从具有复杂频率成分的信号中分离出单一的频率分量，进行幅值和相位分析。

二、 理想滤波器与实际滤波器

1.理想滤波器的频率特性

滤波器实现滤波的功能可以通过滤波器的频率特性来说明。理想滤波器是指，能使通带内信号的幅值和相位都不失真，阻带内的频率成分都衰减为零的滤波器，其通带和阻带之间有明显的分界线。也就是说，理想滤波器在通带内的幅频特性应为常数，相频特性的斜率为常值；在通带外的幅频特性应为零。图5-27表示一理想低通滤波器的幅频及相频特性，其频率响应函数为

图5-27 理想低通滤波器的幅频和相频特性

（a）幅频特性；（b）相频特性

分析式（5-21）表示的频率特性可知，该滤波器在时域内的脉冲响应函数h（t）为sinc函数，图形如图5-28所示。脉冲响应的波形沿横坐标左、右无限延伸，从图中可以看出，在t＝0时刻单位脉冲输入滤波器之前，即在t＜0时，滤波器就已经有响应了。显然，这是一种非因果关系，在物理上是不能实现的。这说明在截止频率处呈现直角锐变的幅频特性，或者说在频域内用矩形窗函数描述的理想滤波器是不可能存在的。实际滤波器的频域图形不会在某个频率上完全截止，而会逐渐衰减并延伸到ω→∞。

图5-28 理想低通滤波器的脉冲响应

图5-29 实际低通滤波器的幅频特性

2.实际滤波器的描述

如上分析，在实际滤波器的幅频特性图中，通带和阻带之间应没有严格的界限。实际低通滤波器的幅频特性如图5-29所示，在通带和阻带之间存在一个过渡带。在过渡带内的频率成分不会被完全抑制，只会受到不同程度的衰减。当然，希望过渡带越窄越好，也就是希望对通带外的频率成分衰减得越快、越多越好。因此，在设计实际滤波器时，总是通过各种方法使其尽量逼近理想滤波器。

与理想滤波器相比，实际滤波器需要用更多的概念和参数去描述它。下面用图5-30所示的实际带通滤波器的幅频特性来说明。

图5-30 实际带通滤波器的幅频特性

（1）通带内的幅频特性用平均值A0来描述。实际滤波器在通带内的幅频特性不像理想滤波器那样平直，而是波动变化的，其波动量d称为波纹幅度。波纹幅度d与平均值A0相比，应越小越好，一般应远小于﹣3dB。

（2）上、下截止频率用﹣3dB截止频率来描述。由于实际滤波器没有明显的截止频率，为了保证通带内的信号幅值不会产生较明显的衰减，一般规定幅频特性值为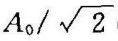时的相应频率值作为带通滤波器的上、下截止频率，这样，通带内信号幅值的衰减量不会超过﹣3dB。相应的通带宽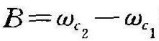称为﹣3dB带宽。

（3）实际滤波器的选择性用倍频程选择性或滤波器因素λ来描述。实际滤波器过渡带幅频曲线的倾斜程度表达了滤波器对通带外频率成分的衰减能力，即选择性。选择性是滤波器的一个重要指标，倍频程选择性和滤波器因素λ就是用来描述过渡带曲线倾斜程度即选择性指标的。

倍频程选择性是指与上、下截止频率处相比，频率变化一倍频程时幅频特性的衰减量，即

或

显然，计算结果的衰减量越大，表示选择性越好。

滤波器因素λ是用带宽的变化来定义选择性的，其含义是滤波器幅频特性值为﹣60dB处的带宽与﹣3dB处的带宽之比值，即

λ愈小，表明滤波器选择性愈好。

（4）实际带通滤波器的分辨力，即分离信号中相邻频率成分的能力，用滤波器品质因素Q来描述。品质因素Q值用滤波器的中心频率ω0与﹣3dB带宽的比值来表达，即

Q值越大，表明分辨力越高。

3.实际带通滤波器的形式

带通滤波器在测试工作中常用来作信号频谱分析。将信号通过幅频特性相同而中心频率不同的多个带通滤波器后，滤波器的输出即可反映信号在该通频带内的幅值和相位信息。

根据带通滤波器带宽B与中心频率f0的关系不同，可分为恒定带宽带通滤波器和恒定百分比带通滤波器。恒定带宽带通滤波器的带宽B为定值，不随中心频率f0变化而变化；恒定百分比带通滤波器的带宽B与中心频率f0的比值（B/f0）始终保持不变，频率愈高，带宽愈宽。这两种带通滤波器的特性如图5-31所示。从特性图可知，在高频区恒定百分比带通滤波器由于带宽增加，分辨力要比恒定带宽带通滤波器差。

恒定百分比带通滤波器通常做成邻接式滤波器来覆盖所需分析的频率范围，对信号进行分段滤波。所谓邻接式，就是前一个滤波器﹣3dB上截止频率即为后一个滤波器﹣3dB下截止频率，首尾相接，各滤波器中心频率是固定和有级变化的。组成邻接式滤波器组最常用的恒定百分比带通滤波器，是1倍频程滤波器和1/3倍频程滤波器，表5-1给出了1倍频程和1/3倍频程滤波器的中心频率f0以及带宽B之值，它们的比值（B/f0）分别为0.71和0.23。

图5-31 两种带通滤波器的特性

（a）恒定带宽带通滤波器； （b）恒定百分比带通滤波器

表5-1 常用倍频程滤波器的参数

续表

为了提高滤波器的分辨力，通常希望用具有恒定带宽的窄带滤波器来覆盖所需分析的频域，但这样做需要很多滤波器才能邻接起来。如果一个窄带滤波器的中心频率可以根据需要在频域上连续变动，对信号进行跟踪滤波，这样，就能实现窄带邻接式滤波器的功能。这类滤波器的中心频率无级变化，称为扫描式滤波器，在第七章振动测量中将作简单介绍。

三、RC模拟式滤波器分析

RC调谐式滤波器是测试系统中常用的一类滤波器，其电路简单，抗干扰能力强。由于RC滤波器低频特性较好，故多用于频率相对不高的信号处理和分析。RC模拟式滤波器分无源滤波器和有源滤波器两类。(www.xing528.com)

1.RC无源滤波器

（1）RC低通滤波器的典型电路和幅频特性如图5-32所示。设输入和输出信号电压分别为ux和uy，电路时间常数τ＝RC。滤波器为一阶系统，其频率响应函数和幅频特性分别为

图5-32 RC低通滤波器

﹣3dB截止频率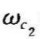＝1/τ

分析该系统特性可知，当输入信号频率ω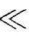1/τ时，A（ω）为常数，信号可以不受衰减地通过滤波器；当ω＝1/τ时，信号衰减﹣3dB；当ω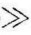1/τ时，信号受到很大衰减。分析可知，在ω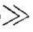1/τ时，H（jω）近似等于1/（jωτ），此时滤波器相当于积分器。

（2）RC高通滤波器的典型电路和幅频特性如图5-33所示。分析电路特性可知，该电路能让高于截止频率的信号通过。RC高通滤波器也是一阶系统，时间常数τ＝RC，其频率响应函数和幅频特性分别为

图5-33 RC高通滤波器

﹣3dB截止频率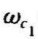＝1/τ

当输入信号频率ω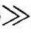1/τ时，A （ω）公1，信号可以不受衰减地通过；当ω＝1/τ时，信号衰减﹣3dB；当ω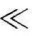1/τ时，幅频特性为衰减段，此时H （jω）≈jωτ，相当于一个微分器。

（3）从RC低通和高通滤波器幅频特性图可知，当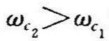时，将两者串联起来，就可以组成RC带通滤波器。考虑到两个串联环节之间存在的负载效应会削弱传输中的信号和改变整个系统的频率响应特性，因此，通常在两个环节之间串入具有高输入阻抗的放大器进行隔离，组成图5-34所示的RC带通滤波器。这实际上将RC无源带通滤波器做成了有源滤波器。

图5-34 RC带通滤波器的组成

RC带通滤波器的频率响应函数由三个环节的频率特性串联而成，即

﹣3dB截止频率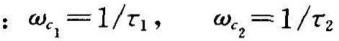

分别调节时间常数τ2和τ1，就可以得到不同的上、下截止频率和带宽B。

当高通滤波器的下截止频率ωc1大于低通滤波器的上截止频率ωc2时，将它们并联起来就组成了RC带阻滤波器，其电路图如图5-35所示。

图5-35 RC带阻滤波器

2.RC有源滤波器

上述仅由阻容元件组成的RC无源滤波器，具有线路简单、体积小、成本低的优点，但它们都是低阶系统，由于过渡带衰减缓慢（一阶滤波器过渡带斜率为﹣20dB/dec），因此选择性差。将几个一阶滤波器串联起来可以提高阶次，但级间耦合的负载效应会使信号逐级减弱。采用有源滤波器可以克服这些缺点。RC有源滤波器是用RC无源网络和运算放大器等有源器件结合在一起构成的。其特点：一是可以放大信号；二是具有高输入阻抗的运算放大器可以进行级间隔离，消除或减小负载效应的影响。这样，有源滤波器可以多级串联组成高阶滤波器，从而明显地提高了滤波器的选择性。

（1）根据RC网络与运算放大器的联接方式，一阶RC有源低通滤波器有两种形式。

图5-36（a）所示的是将RC低通网络直接接到运算放大器的输入端，组成RC有源低通滤波器，其输出特性推导如下：

图5-36 一阶RC有源低通滤波器

设滤波器输入端电压为ux，输出端电压为uy，运算放大器输入端电压为u。忽略通过放大器的电流，则对反相输入端，由于流经R1和RF的电流相等，故可求出

R1uy＝（R1＋RF）u 　　（5-31）

对同相输入端，由于流经R、C元件的电流相等，故可求出

Zcux＝（R＋Zc）u 　（5-32）

将两式相除，得到输出、输入关系为

代入Zc＝1/（jωC），将输出特性转换到频域，得到频率响应函数为

可见，与无源滤波器相比，该低通滤波器将信号放大了（1＋RF/R1）倍，﹣3dB截止频率仍为ωc＝1/（RC）。

图5-36（b）是将RC高通网络接入运算放大器的负反馈通道而形成的RC有源低通滤波器。由比例器的输出特性可得到

式中，

因此，该滤波器的频率响应函数为

这种接法的滤波器放大倍数为RF/R1，﹣3dB截止频率ωc＝1/ （RFC）。

（2）为了改善滤波器的选择性、增大通频带以外信号的衰减量，应提高滤波器的阶次。二阶有源低通滤波器可由前述的两种一阶低通滤波器组合而成，如图5-37所示。其中，图（a）是简单的组合，图（b）是改进后的组合，由于形成了多路负反馈，滤波器特性更好些。二阶低通滤波器幅频特性高频段的斜率为﹣40dB/dec，其衰减量比一阶低通滤波器大，故选择性要好。滤波器串接得愈多，则阶次愈高，其幅频特性愈逼近理想特性，但相频特性非线性会增加。

图5-37 二阶RC有源低通滤波器

在设计实际滤波器时，除了考虑滤波器的阶次外（即要求过渡带窄），还要考虑通频带内幅频特性的波动情况和相频特性。工程中可实现的典型低通滤波器类型有巴特沃思滤波器和切比雪夫滤波器，这两类滤波器各有所长。如前所述，高通滤波器、带通滤波器和带阻滤波器都可以通过低通滤波器频率特性的变换来设计，这方面内容可参考其他有关书籍。

四、 数字滤波器简介

利用数字技术分析和处理信号时，面对的将是由模拟信号转换而来的离散数字信号。有关模数转换的知识将在下一节作介绍。所谓数字滤波，就是通过一定的计算方法和计算程序对离散信号进行加工，将其改造成为所要求的离散信号，例如，使其中有用的信号成分被增强，各种干扰和噪声被消除或削弱。与模拟滤波器相似，数字滤波器也有低通、高通、带通与带阻之分。数字滤波方法是在模拟滤波方法的基础上发展起来的，它是对模拟滤波的一种模拟。因此，各类模拟滤波器的数学模型都是数字滤波器设计的基础。下面用低通滤波器来说明这种模拟过程。

对图5-32所示的RC低通滤波器，其输出与输入的关系可推导为

用数字技术处理信号时，要对输入的模拟电压ux进行采样，使其离散化，这样，滤波的结果uy也应是离散值。设信号的离散值为

uxn＝ux（n，Δt）， uyn＝uy（n，Δt） 　（5-38）

式中，n为采样序号；Δt为采样间隔。

当采样间隔足够小时，根据导数的定义，式（5-37）可以用离散值表示为

即

整理得 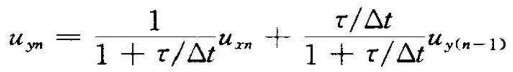　（5-39）

按上式表达的计算过程编写程序对输入的离散信号uxn进行运算，就会得到原RC低通滤波器的滤波效果，uyn即为经过低通滤波后的数字输出信号。

在上述滤波方法中，由于第n次采样值uxn的计算要用到前一次采样值的计算结果uy（n－1），因此这种滤波方法称为递归型滤波。数字滤波的计算方法各种各样，一般根据被测参量变化的特征和对被测信号改造的要求，可以选择或编出所需的数字滤波计算方法和程序。从系统的观点来看，在时域中滤波器的输出yn等于输入xn与滤波器脉冲响应h（n）的卷积，即

yn＝xn*h（n）　（5-40）

可见，只要改变滤波器的数学模型h（n），就可以得到具有各种特性的滤波器，从而得到所需的输出yn。

与模拟滤波器相比，数字滤波精度高，可靠性高，不存在阻抗匹配问题；使用灵活、方便，滤波器参数可以根据需要修改；特别是能处理频率很低的信号，这对模拟滤波器来说几乎是不可能的。但由于运算程序需要一定时间，运算速度不能做得很高，因而不能处理频率很高的信号。数字滤波还可以采用硬件来实现，即根据计算要求，将各种数字运算电路联接起来，构成数字滤波运算器。随着大规模集成电路技术的发展，数字滤波速度问题将会得到解决。数字滤波可以时分复用，一套数字滤波运算器或一段数字滤波程序可以供多个测量通道共用，从而降低了成本。

数字滤波器主要用于由微型计算机组成的自动测试和信号处理系统以及计算机控制系统中。若在数字滤波器前后配置模数转换器和数模转换器，则其作用相当于模拟滤波器，也可以直接处理模拟信号。