电阻式传感器：测量线位移和角位移的理想选择

电阻式传感器是一类根据电阻定律而设计的传感器，它能将被测物理量（如位移、力等）的变化转换为电阻的变化输出。按引起传感器电阻变化的参数不同，可以将该传感器分为电位计（器）式传感器和电阻应变式传感器两大类。

一、电位计（器）式传感器

电位计式传感器又称变阻器式传感器。常用的电位计式传感器有直线位移型、角位移型和非线性型等，其结构如图3-2所示。不管是哪种类型的传感器，都由线圈、骨架和滑动触头等组成。线圈绕于骨架上，触头可在绕线上滑动，当滑动触头在绕线上的位置改变时，即实现了将位

图3-2 电位计式传感器

（a）直线位移型；（b）角位移型；（c）非线性型

移变化转换为电阻变化。根据电阻定律：

式中，ρ为电阻率（Ω·mm2/m）；l为电阻丝长度（m）；A为电阻丝截面积（mm2）。

上式说明，如果电阻丝直径与材质一定时，则电阻值的大小随电阻丝的长度l而变化。

直线位移型电位计（器）式传感器如图3-2（a）所示，当被测直线位移变化时，滑动触头的触点C沿电位计移动，若移动x，则C点与A点之间的电阻为

Rx＝Rlx　（3-2）

式中，Rl为单位长度的电阻值。

传感器的灵敏度

当骨架为等截面均匀的导线时，S为常数。

直线位移型电位计式传感器的输出（电阻）与输入（位移）呈线性关系。

角位移型电位计式传感器如图3-2（b）所示，其输出阻值的大小随角度位移的大小而变化，该传感器的灵敏度为

式中，α为转角（弧度）；k。为单位弧度对应的电阻值。

非线性电位计式传感器如图3-2（c）所示。当输入位移呈非线性变化规律时，为了保证输入、输出的线性关系，利于后续仪表的设计，可以根据输入的函数规律来确定这种传感器的骨架形状。例如，若输入量为f（x）＝Rx2，则为了得到输出的电阻值R（x）与输入量f（x）呈线性关系，电位计的骨架应采用三角形；若输入量为f（x）＝Rx3，则电位计的骨架应采用抛物线形。

电位计式传感器一般采用电阻分压电路，将电参量R转换为电压输出给后续电路，如图3-3所示。当触头移动x距离后，输出电压uy可用下式计算：

式中，RP为电位计的总电阻；xP为电位计的总长度；RL为后续电路的输入电阻。

图3-3 电阻分压电路

式（3-5）表明，传感器经过后续电路后的实际输出、输入为非线性关系，为减小后续电路的影响，应使RL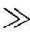RP。此时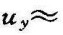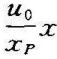，，近似为线性关系。

电位计式传感器用于线位移和角位移的测量，常用于伺服记录仪或电子电位差计等。

电位计式传感器的优点是结构简单，性能稳定，使用方便。其缺点是分辨率不高，由于受到骨架尺寸和导线直径的限制，分辨力很难高于20μm，由于滑臂机构的影响，使用频率范围也受到限制。它们还有电噪声较大、绕制困难等缺点。

二、电阻应变式传感器

通过应变片将被测物理量（如应变、力、位移、加速度、扭矩等）转换成电阻变化的器件称为电阻应变式传感器。由于电阻应变式传感器具有结构简单、体积小、使用方便、动态响应快、测量精确度高等优点，因而被广泛应用于航天、机械、电力、化工、建筑、纺织、医学等领域，成为目前应用最广泛的传感器之一。

1.金属电阻应变片

电阻应变式传感器的敏感元件是应变片。应变片主要分金属电阻应变片和半导体应变片两类。

金属电阻应变片分丝式、箔式两种。

金属丝电阻应变片（或称电阻丝式应变片）出现较早，现仍在广泛使用，其典型结构如图3-4所示。它主要由具有高电阻率的金属丝绕成的敏感栅、基底、覆盖层和引线等组成。

金属箔式电阻应变片的敏感栅，则是用栅状金属箔片代替栅状金属丝。金属箔栅采用光刻技术制造，适用于大批量生产。由于金属箔式电阻应变片具有线条均匀、尺寸准确、阻值一致性好、传递试件应变性能好等优点，因此，目前使用的多为金属箔式应变片，其结构形式如图3-5所示。

图3-4 金属丝应变片

1—覆盖层；2—基底；3—敏感栅（电阻丝）；4—粘结剂层；5—引线

金属电阻应变片的工作原理，是基于金属导体的应变-电阻效应。即当应变片粘贴于被测构件的表面时，在外力作用下，应变片敏感栅随构件一起变形，其电阻值发生相应的变化，由此可将被测量转换成电阻的变化。由式（3-1）得知，当敏感栅发生变形时，其l、ρ、A均将变化，从而引起R的变化。当每一可变参数分别有一增量dl、dρ、d A时，所引起的电阻增量为

式中，A＝πr2，r是电阻丝半径。则上式为

图3-5 典型箔式应变片

（a）单丝栅式；（b）双丝栅式；（c）三丝栅式；（d）多丝栅式

电阻的相对变化为

式中，dl/l＝ε为电阻丝轴向相对变形，或称纵向应变；dr/r为电阻丝径向相对变形，或称横向应变。

当电阻丝轴向伸长时，必然沿径向缩小，两者之间的关系为

式中，μ为电阻丝材料的泊桑比；dρ/ρ为电阻丝电阻率的相对变化。(www.xing528.com)

dρ/ρ与电阻丝轴向所受正应力σ有关，即

dρ/ρ＝λσ＝λEε 　（3-9）

式中，E为电阻丝材料的弹性模量；λ为压阻系数，与材质有关。

将式（3-8）、式（3-9）代入式（3-7），得

dR/R＝（1＋2μ＋λE）ε 　（3-10）

式（3-10）中，（1＋2μ）ε项由电阻丝的几何尺寸改变所引起。对于同一电阻材料，（1＋2μ）是常数。λEε项由电阻丝的电阻率随应变的改变所引起。对于金属材料来说，λE很小，可以忽略不计，所以上式可简化为

dR/R≈（1＋2μ）ε 　（3-11）

其灵敏度（又称应变片的灵敏系数）为

将式（3-12）代入式（3-11），则得

dR/R＝Sε　（3-13）

由于测试中R的变化量微小，可认为dR≈ΔR，则式（3-13）可表示为

ΔR/R＝Sε 　（3-14）

常用的灵敏度S在1.7～3.6之间。

在测试中，选用金属电阻应变片应注意以下两点：

（1）应变片电阻值的选择，应变片的原电阻值一般有60、90、120、200、300、500、1000Ω等。当选配动态应变仪组成测试系统进行测试时，由于动态应变仪电桥的固定电阻为120Ω，因此为了避免对测量结果进行修正计算，以及在没有特殊要求的情况下，选择120Ω的应变片为宜。除此以外，可根据测量的要求选择其他阻值的应变片。

（2）应变片灵敏度的选择，当选配动态应变仪进行测量时，应选用S＝2的应变片。由于静态应变仪配有灵敏度的调节装置，故允许选用S≠2的应变片。对于那些不配用应变仪的测试，应变片的S值愈大，输出也愈大。因此，往往选用S值较大的应变片。

2.半导体应变片

半导体应变片的典型结构如图3-6所示，它主要由胶膜基片、半导体敏感栅、内外引线、焊接电极板等组成。

半导体应变片的工作原理是基于半导体材料的压阻效应。所谓压阻效应，是指单晶半导体材料沿某一轴向受到外力作用时，其电阻率ρ发生变化的现象。

图3-6 半导体应变片

1—胶膜衬底；2—P-Si；3—内引线；4—焊接板；5—外引线

从半导体物理性质可知，半导体在压力、温度及光辐射作用下，能使其电阻率ρ发生很大的变化。因此由分析式（3-10）得知，式中由电阻率变化引起的λEε远大于由几何形变引起的（1＋2μ） ε，对于半导体应变片，式中的（1＋2μ）ε可以忽略，故其电阻变化率为

dR/R＝λEε 　（3-15）

灵敏度为

半导体应变片的灵敏度比金属电阻应变片大50～70倍。

从以上分析表明，金属电阻应变片与半导体应变片的主要区别在于：前者是利用导体的形变引起电阻的变化，而后者则是利用半导体材料的电阻率变化引起电阻的变化。

半导体应变片突出的优点是灵敏度高、机械滞后小、横向效应小、体积小，这些优点为其广泛应用提供了条件。其缺点是对温度的稳定性能差。当灵敏度、离散度大时，以及在较大应变作用下，会使应变片的非线性误差大，这一点给使用带来了一定的困难。

目前国产的半导体应变片大都采用P型硅单晶材料制作。随着集成电路技术和薄膜技术的发展，近年来已研制出在同一硅片上制作扩散型应变片和集成电路放大器等，即集成应变组件。这将对在自动控制与检测中采用微处理技术起到一定的推动作用。

三、电阻应变式传感器的应用举例

电阻应变式传感器应用很广，可概括为以下两个方面。

（1）将应变片粘贴于被测构件上，直接用来测定构件的应变或应力。例如，为了研究或验证机械、桥梁、建筑等某些构件在工作状态下的受力、变形情况，可利用形状不同的应变片，粘贴在构件的预测部位，可测得构件的拉、压应力、扭矩或弯矩等，从而为结构设计、应力校核或构件破坏的预测等提供可靠的实验数据。图3-7示出了两种实用例子。

（2）将应变片粘贴于弹性元件上，与弹性元件一起构成应变式传感器。这种传感器常用来测量力、位移、压力、加速度等物理参数。在这种情况下，弹性元件将得到与被测量成正比的应变，再通过应变片转换为电阻的变化后输出。典型应用如图3-8所示。其中，图（a）所示的加速度传感器由悬臂梁、质量块、基座组成。测量时，基座固定在振动体上。振动加速度使质量块产生惯性力，悬臂梁则相当于惯性系统的“弹簧”，在惯性力的作用下产生弯曲变形。因此，梁的应变在一定的频率范围内与振动体的加速度成正比。图（b）所示为纱线张力检测装置，检测辊4通过连杆5与悬臂梁2的自由端相连，连杆5同阻尼器6的活塞相连，纱线7通过导线辊3与检测辊4接触。当纱线张力变化时，悬臂梁随之变形，使应变片1的阻值变化，并通过电桥将其转换为电压的变化后输出。

图3-7 构件应力测定的应用举例

（a）测齿轮轮齿弯矩；（b）测立柱应力

图3-8 典型应变式传感器

（a）加速度传感器；（b）动态张力传感器

1—应变片；2—悬臂梁；3—导线辊；4—检测辊；5—连杆；6—阻尼器；7—纱线

在应用电阻应变式传感器时，还应特别注意机械滞后、蠕变、零漂、绝缘电阻等问题。出现这些问题的原因往往与应变片的粘贴工艺有关，如粘结剂的选择、粘贴技术、应变片的保护等。