如何进行不失真测试的优化条件？

一、定义

设测试装置的输入x（t）与输出y（t）满足方程

y（t）＝A0x（t－t0） 　（2-38）

式中，A0和t0均为常量，则称此测试装置为不失真测试装置。可见，对于不失真测试装置，输出与输入相比较，只是幅值放大了A0倍，时间延迟了t0而已，其波形完全相似。

对式（2-38）两边取拉普拉斯变换，得

于是得不失真测试装置的传递函数为

频率响应函数为

其幅频与相频特性分别为

A（ω）＝|H（jω）|＝A0　（常数）　（2-41）(www.xing528.com)

＝∠H（jω）＝﹣t0ω　（直线）　（2-42）

可见，要实现不失真测试，测试装置的幅频特性应为常数，相频特性应为直线（线性）。A（ω）不等于常量引起的失真称为幅值失真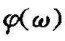，与ω之间的非线性关系引起的失真称为相位失真。

二、测试装置的不失真测试的频率范围

实际测试装置在ω∈（0，∞）的整个频率轴上并不满足式（2-41）与式（2-42）两个不失真测试的条件，但在一定频段上却可视为近似满足，下面将加以讨论。

1.一阶装置不失真测试的频率范围

从一阶装置的幅频、相频特性曲线图2-12（b）中可看出，当ω＝1/r时，A（ω）已衰减了近30％，故实际不失真测试的频率范围为ωω∈（0，ωmax），且ωmax＜1/τ。显而易见，一阶装置的时间常数τ愈小，不失真测试的频率范围愈宽。

2.二阶装置不失真测试的频率范围

计算表明，当二阶装置的阻尼比ζ＝0.7时，在ωω∈（0，0.58ωn）的频率范围内，幅频特性A（ω）的变化不超过5％，同时相频特性（ω）也接近于直线，产生的相位失真也很小。从不失真测试的角度看，二阶装置的固有频率ωn愈大，则不失真测试的频率范围愈宽。但ωn增大，往往是靠加大系统的刚度k来实现的，系统的灵敏度S∞1/k（参见式（2-19）中的S的表达式），所以ωn增大会导致测试装置的灵敏度下降。故选用时，只要固有频率足够用即可，不要一味追求高固有频率。