非周期信号的特征分析

一、非周期信号的频谱特征

非周期信号x（t）可以看成是由某个周期信号xT（t）当T→∞时转化而来的。为了说明这一点，作周期为T的信号xT（t），使其在（﹣T/2，T/2）之内等于x（t），而在（﹣T/2，T/2）之外按周期T延拓出去，如图1-5所示。

图1-5 非周期信号与周期信号的关系

（a）非周期信号；（b）周期信号

T越大，xT（t）与x（t）相等的范围也就越大，当T→∞时，周期信号xT（t）便转化为非周期信号x（t），即

把式（1-7）与式（1-8）代入式（1-16）得

由于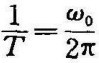，代入上式得

则式（1-17）可改写成

上式右端可以看成是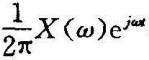在（﹣∞，∞）上对ω的积分，即

将式（1-18）代入式（1-19）得

若把ω＝2πf代入上式，则有

上式称为信号x（t）的傅里叶积分公式。现在不加证明地给出下面的傅里叶积分定理。

傅里叶积分定理 若x（t）在（﹣∞，∞）上满足下列条件：1°x（t）在任一有限区间上满足狄利克雷条件；2°x（t）在无限区间（﹣∞，∞）上绝对可积，即积分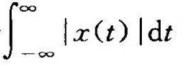收敛，则有

成立。（左端的x（t）在它的间断点t处，应以（x（t＋0）＋x（t－0））/2来代替）

在式（1-20）中，令

则式（1-20）可写成

观察式（1-21）与式（1-22），不难看出它们构成了一种变换对，即

这一变换对称为傅里叶变换对。式（1-21）称为x（t）的傅里叶变换，并记为

X（f）叫做x（t）的傅里叶像函数。

式（1-22）称为x（t）的傅里叶逆变换，并记为

x（t）称为X（f）的傅里叶像原函数（像与像原就像一面镜子一样，故此得名）。

一般X（f）是实变量f的复函数，可以写成

是X（f）的实部，由于ReX（f）＝ReX（﹣f），所以ReX（f）是频率f的偶函数；

是X（f）的虚部，由于ImX（f）＝﹣ImX（﹣f），所以ImX（f）是f的奇函数；

是X（f）的模，由于|X（f）|＝|X（﹣f）|，所以|X（f）|是f的偶函数；

是X（f）的相位，由于∠X（f）＝﹣∠X（﹣f），所以∠X（f）是f的奇函数。

总而言之，傅里叶变换X（f）具有实偶虚奇（实部为偶函数，虚部为奇函数），模偶相奇（模为偶函数，相位为奇函数）的特征。

为了说明X（f）的含义，把式（1-22）进一步写成：

由于|X（﹣f）|sin（﹣2πft＋∠X（﹣f））＝﹣X（f）|sin（2πft＋∠X（f）），故上式右端第二项积分为零，从而有

式（1-27）清楚地表明了|X（f）|与∠X（f）的物理含义，即|X（f）|df是谐波信号的幅值，|X（f）|是谐波信号的幅值在频率f上的分布，即单位频宽上的幅值，称为幅值谱密度，常简称为幅值谱；∠X（f）是谐波信号的初相位。两者均是连续谱，X（f）常称为频谱函数。

式（1-27）同时也说明，非周期信号仍然可以分解成谐波信号的叠加。与周期信号分解的不同之处在于，各谐波信号的频率是连续分布的，而不是离散的。这再一次表明：谐波信号是最基本的信号。

例1-3 求矩形窗函数ωR（t）的频谱函数，并绘出其图形。

解 矩形窗函数ωR（t）的定义为

其频谱函数为

在上式中定义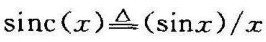，该函数在信号分析中很有用。矩形窗函数的频谱如图1-6所示。

图1-6表明了矩形窗函数的谐波成分分布情况。但请读者注意，由傅里叶变换得到的幅值谱实为幅值谱密度。

二、傅里叶变换的主要性质

傅里叶变换有许多重要性质，了解它们，可以帮助我们掌握信号的时域与频域之间的对应关系及转换规律，更快速地求得信号的频谱函数。

图1-6 矩形窗函数及其频谱

1.奇偶虚实性质

实函数x（t）的傅里叶变换X（f）的实部ReX（f）为偶函数，虚部ImX（f）为奇函数。X（f）的模|X（f）|为偶函数，相位∠X（f）为奇函数。

如果x（t）为偶函数，则ImX（f）＝0，X（f）将是实偶函数，即X（f）＝ReX（f）。

如果x（t）为奇函数，则ReX（f）＝0，X（f）将是虚奇函数，即X（f）＝jImX（f）。

了解这个性质可以减少不必要的变换计算。

2.线性叠加性质

傅里叶变换是一种线性运算，满足线性叠加性质。

若　x1（t）X1（f），x2（t）X2（f）

则 c1x1（t）＋c2x2（t）c1x1（f）＋c2X2（f）（c1，c2为常数）

3.对称性质

若　x（t）X（f）

则 　X（t）x（﹣f）

证

以﹣t替代t，则有

将t与f互换，则上式变为

所以　X（t）x（﹣f）

应用这个性质，可以避开复杂的积分运算，利用已知的傅里叶变换对，获得相应对称的变换对。

例1-4 求x（t）＝sinc（t）＝（sint）/t的傅里叶变换。

解 已知变换对

由对称性质有

令τ＝1/π，则

sinc（t）的频谱如图1-7所示。

比较图1-6与图1-7，可以体会对称性质的含义。

图1-7 sinc（t）及其频谱

4. 时间尺度改变性质

在时间信号x（t）的幅值不变的条件下，若x（t）X（f），则

证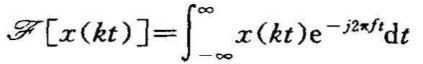

作变量代换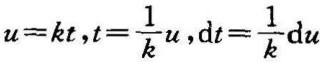，则

当时间尺度压缩（k＞1）时，频谱的频带加宽，幅值减小；当时间尺度扩展（k＜1）时，其频谱变窄，幅值增大。

图1-8以矩形窗函数为例，表明时间尺度变化对应的频域图形的变化情况。

图1-8 时间尺度改变性质

时间尺度改变性质在工程中常常得到应用。例如，在记录爆炸信号及瞬态冲击信号时，为了便于计算机采集数据及降低对后续处理设备通频带上限的要求，可采用记录磁带快录慢放的方法改变时间尺度。

5.时移性质

若　x（t）X（f）

则　　（t0为常数）

证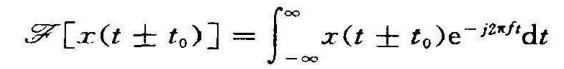　

令u＝±t0，t＝u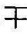t0，dt＝du，上式变为

此性质表明，在时域中信号沿时间轴平移一个常值t0时，频谱函数将乘上因子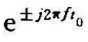，仅改变相位谱，而不改变幅值谱。

6.频移性质

若 　x（t）X（f）

则　　（f0为常数）

证明过程同上，略。

可见，若频谱沿频率轴平移f0，则时域信号为原信号乘以相应的因子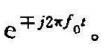

7.卷积定理

两函数x1（t）与x2（t）的卷积记为x1（t）*x2（t），其定义为

卷积满足：

1°交换律

x1（t）*x2（t）＝x2（t）*x1（t）

2°结合律

x1（t）* [x2（t）*x3（t）] ＝[x1（t）*x2（t）] *x3（t）

3°分配律

x1（t）*[x2（t）＋x3（t）]＝x1（t）*x2（t）＋x1（t）*x3（t）

在信号分析以及经典控制理论中应用十分广泛的是卷积定理。

卷积定理 若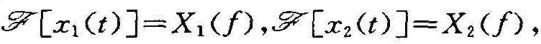则

证 先证时域卷积定理：

由对称性不难得到频域卷积定理。

8.微分性质

若x（t）X（f），且当|t|→∞时，x（t）＝0，则

证(www.xing528.com)

两边对t求导得

即

推论

9.积分性质

若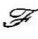[x（t）＝X（f）

则

证令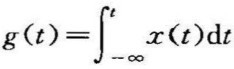，有g′（t）＝x（t），两边取傅里叶变换得

推论 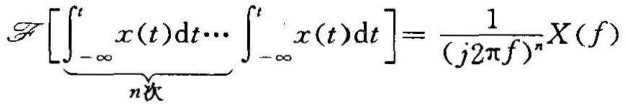　（1-36）

在振动测试中，如果测得振动系统的位移、速度或加速度中任一参数，应用微分、积分性质就可以获得其他参数的频谱。

三、单位脉冲函数（δ函数）及其频谱

1.δ函数的定义

δ函数是一种广义函数，它的定义为

式（1-37）与式（1-38）联合起来构成δ函数的定义。（在普通函数中，仅在一个点上取不为零数值的函数其面积等于零）

2.δ函数的物理背景说明

图1-9所示为锤头冲击钢板的情况，其冲击力为f（t）。设锤头与钢板间的冲击接触时间为ε，则当t＜0或t＞ε时，f（t）＝0，f（t）仅在0＜t＜ε内的短时间内存在，其表达式为

图1-9 冲激力的描述

设mv＝1（单位动量），则有

显然，f（t）的面积（即冲量）恒等于动量的改变，即

若锤头和钢板均为绝对刚体，则ε→0，式（1-39）与式（1-40）即为δ函数的定义式，说明绝对刚体间的冲击力f（t）为δ函数。

f（t）与δ（t）的图形如图1-10所示，其中δ函数图中标注的数值1表示其积分值。

图1-10 冲击力f（t）与δ函数

3.δ函数的性质

1）乘积性质

x（t）为任一连续信号，则有

x（t）δ（t）＝x（0）δ（t）　（1-41）

x（t）δ（t－t0）＝x（t0）δ（t－t0）　（1-42）

计算等式左、右两边的取值和面积值，很容易验证上述二式。

2）筛选性质

式（1-43）与式（1-44）称为δ函数的筛选性质，也称采样性质，用得较多。有些书中将式（1-44）作为δ函数的定义式。

3）卷积性质

x（t）*δ（t）＝x（t）　（1-45）

x（t）*δ（t－t0）＝x（t－t0）　（1-46）

证

式（1-45）与式（1-46）称为δ函数的卷积性质。卷积性质表明，函数x（t）和脉冲函数的卷积的结果，就是将x（t）在t轴上平移到脉冲发生处。可见，与δ函数作卷积运算，就是进行图形搬迁。

例1-5 求x（t）*[δ（t＋T）＋δ（t－T）]，其中x（t）如图1-11所示。

解 x（t）*[δ（t＋T）＋δ（t－T）]＝x（t）*δ（t＋T）＋x（t）*δ（t－T）＝x（t＋T）＋x（t－T）

4.δ函数的频谱

将δ（t）进行傅里叶变换

图1-11 δ函数的卷积性质

式（1-47）为δ函数的频谱，如图1-12所示。从图中可知，时域的脉冲函数具有无限宽广的频

图1-12 δ函数及其频谱

谱，而且在所有的频段上都是等强度的。δ函数的这一频谱特征具有广泛的工程应用价值。如用试验的方法求某一振动系统的固有频率时，常对系统进行各种不同频率的激励（激励的幅值不变），并通过传感器获得系统对不同频率激励的响应。若外激励频率恰好等于系统的固有频率，则响应幅值最大，由此获知系统固有频率。但这种试验方法每改变一次激励频率，就需测试一次，效率很低；而采用脉冲信号输入（例如锤击），只需一次试验，即可获得系统的固有频率，效率较高。日常生活中，敲击西瓜（即脉冲输入，相当于各种频率的谐波信号一次输入进去），听其回声（即西瓜对各种不同频率谐波信号的响应），就可判断西瓜的状态（生或熟）。

对式（1-47）求逆变换得

对于不满足绝对可积条件的函数，例如常数、复指数函数、正弦函数、余弦函数等，在进行傅里叶变换时，需用到式（1-48），其具体求解过程参见常用信号的傅里叶变换。

四、常用信号的频谱函数

1.矩形窗函数及其频谱（见例1-3）

2.δ函数及其频谱（见式（1-47））

3.常数函数x（t）＝1的频谱

由傅里叶变换的定义有

由式（1-48）得

X（f）＝δ（﹣f）

δ函数为偶函数，故有

X（f）＝δ（f）　（1-49）

由傅里叶变换的对称性质也可得到常数1的傅里叶变换：

因为　δ（t）1

所以　1δ（﹣f）＝δ（f）

其频谱如图1-13所示。常数1的傅里叶变换δ（f）为其幅值谱密度，说明仅含有直流成分，其幅值在频率轴上的分布密度为无穷大，但直流成分的幅值仍为有限值1。很明显，若不引入δ函数，则无法描述这种集中分布的函数特征。

图1-13 常数及其频谱

4.复指数函数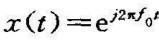的频谱

由傅里叶变换的定义有

根据式（1-48），上式变为

X（f）＝δ（f﹣f0）　（1-50）

由傅里叶变换的频移性质也可得到复指数函数的频谱；

因为 　1δ（f）

所以　

5.正弦函数的频谱

由欧拉公式有

根据式（1-50）得

6.余弦函数的频谱

由欧拉公式有

根据式（1-50）得

正、余弦函数的频谱如图1-14所示。

图1-14 正、余弦函数及其频谱

正、余弦函数的傅里叶变换均为δ函数（在±f0处为无穷大）。这是因为，正、余弦函数只含有单一的频率成分f0，其幅值为1，幅值沿频率轴的分布密度即为δ函数。

7.符号函数sgn（t）及其频谱函数

符号函数sgn（t）的定义式为

不难看出，其频谱函数SGN（f）为

所以

符号函数sgn（t）及其频谱如图1-15所示。

图1-15 符号函数及其频谱

8.单位阶跃函数u（t）及其频谱

单位阶跃函数u（t）可写成

由此可得

单位阶跃函数u（t）及其频谱如图1-16所示。

图1-16 单位阶跃函数及其频谱

9.一般周期信号的傅里叶变换

一般周期信号x（t）既可展成傅里叶级数来表示其频谱特征，即

也可对x（t）求傅里叶变换

其频谱的一般图形如图1-17所示，为离散谱，含有δ函数。

10.周期单位脉冲序列g（t）及其频谱

周期单位脉冲序列g（t）的表达式为

为套用式（1-56），先求f0及cn：

图1-17 一般周期函数的傅里叶变换谱

所以

周期单位脉冲序列g（t）及其频谱如图1-18所示。

图1-18 周期单位脉冲序列及其频谱