使用游标卡尺与测微计测量零件尺寸的操作流程及示例

飞片是在炸药微装药与其他微装药之间的间隙中设置的金属片，是以金属片飞行动能传递爆炸能量的元件。由于飞片与炸药之间是被加速膛隔开的，同时炸药中不含敏感药剂，起爆阈值能量高，对机械冲击、静电、杂散电流、射频等的抵抗能力强，是一种安全和可靠的起爆方式。

5.2.3.1 飞片起爆机理分析

飞片起爆技术是指利用施主装药爆轰驱动飞片，通过一定长度的空气间隙（也即加速膛）冲击起爆下一级炸药。这种起爆方式的特点是加速膛的长度是依据飞片的材料、质量和上一级炸药释放的能量进行严格设计的，使得飞片在一定能量的条件下被加速到极限速度。装药驱动飞片进行能量传递的过程中，飞片的能量主要是以动能形式存在，而动能与速度的平方成比例。因此，研究飞片的最大速度具有重要意义。图5.50所示为典型的飞片起爆结构。

图5.50　典型的飞片起爆结构

5.2.3.2 飞片速度的影响因素

1. 加速膛长度

加速膛的长度对飞片获得最大速度起着重要作用，当飞片被炸药驱动在加速膛运动时，飞片不断地被加速，一定程度上加速膛的长度决定了飞片最终获得的速度。如果加速膛长度较小，飞片就不能达到它的极限速度；如果加速膛长度太大，飞片在飞行过程中不断压缩前方的空气，使得飞片速度减小。

2. 约束强度

通过研究初级装药约束壳体对不同材料和尺寸的飞片速度的影响，得出装药直径和飞片直径较小时，受约束壳体厚度变化的影响较显著，主要是因为装药直径小时，容易受稀疏波的影响；飞片厚度较小时，飞片速度受约束壳体影响比较小。通过比较验证了约束壳体的厚度选取为0.2 mm是合适的。

3. 飞片尺寸

在初级药量一定的条件下，飞片速度随飞片厚度的增加而逐渐较小，减小的幅值与飞片的厚度有关，飞片厚度较小时，其下降趋势较显著；对于厚度相同的飞片，直径小的飞片速度明显大于直径大的飞片速度，主要原因是飞片厚度相同时，直径小的飞片质量小，在初级药量一定的条件下，获得的速度就大。

4. 飞片材料

相同药量的炸药驱动尺寸相同但是材料不同的飞片，其获得的速度不相同，通过实验比较可以得出，尺寸相同的飞片，材料密度小的飞片的速度大，材料密度大的飞片速度小。

5.2.3.3 装药驱动飞片速度实验研究

实验研究飞片速度的方法主要有有机玻璃台阶法、VISAR（Velocity Interferometer System for Any Reflector）法和法布里-珀罗激光干涉法等[11]。VISAR法测试精度较高，理论上可达10 m/s，而且可以测得飞片在爆轰驱动下飞行的速度历史，近年来国内学者利用VISAR法对不同条件下的飞片速度进行了大量研究，但VISAR法也存在缺点：对飞片表面的光反射率要求较高，测试系统操作比较复杂，光纤探头价格昂贵且容易损坏。本章基于法拉第电磁感应定律，设计加工了以高磁场强度的永磁装置，采用以此为主要测量仪器的电磁法测试了火工品小型施主装药驱动不同金属飞片的速度变化规律，并利用VISAR法对电磁法进行了标定，结果证明电磁法测得的实验结果是可靠的，电磁法还具有操作简单、实验成本低的特点。

1. 测试原理

电磁法测试飞片平均速度的主要依据是法拉第电磁感应定律和应力波理论，用电磁速度传感器直接测量爆轰波驱动飞片在一段飞行距离的平均速度。基本原理：利用法拉第电磁感应定律可知，当金属导体在磁场中做切割磁力线运动时，就会在导体的运动部位产生感应电动势，如果导体形成闭合回路，则产生感应电流。如图5.51所示，其电动势的大小与导线所包围面积的磁通量对时间的变化率成正比，即

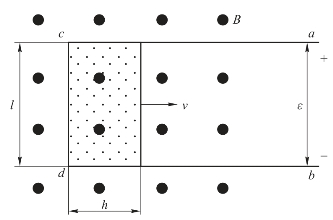
图5.51　永磁场中矩形线圈感应电流的极性

式中，ε为感应电动势（V）；Ф为线圈的磁通量（Wb）；t为时间（s）。

由于磁通量Φ=BS，式（5-111）可写成

式中，B为磁感应强度（T）；S为金属导体切割磁力线的面积（mm2）。

当导体处于恒定磁场中时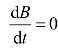，，由式（5-112）可得

式中，l为移动导体cd的长度（mm）；v为导体cd切割磁力线的速度（mm/μs）。正号表示原矩形框所包围的面积增加，负号表示原矩形框所包围的面积减小。

由式（5-113）可知，当其他参数一定时，磁场强度越大，则产生的感应电动势越强，本章研究的是装药直径小于5 mm的施主装药，其驱动飞片的能力相对于大直径装药要弱得多，为了提高感应电动势的信号强度，设计制作的永磁场的磁场强度为0.23 T，比文献中的0.05～0.1 T提高了一倍以上，保证了测试信号的灵敏度。

电磁速度传感器的结构如图5.52所示，其主要部件包括铜箔、有机玻璃板、有机玻璃条、有机玻璃块和聚酰亚胺膜。各部件用胶水黏合，保证铜箔绕成有效的闭合回路。

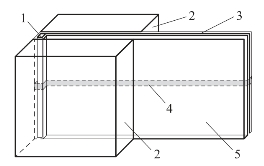
图5.52　电磁速度传感器结构图

1—有机玻璃条；2—有机玻璃块；3—聚酰亚胺膜；4—铜箔；5—有机玻璃板

2. 实验装置与测试系统

电磁法测试施主装药爆炸驱动飞片平均速度的测试系统连接框图如图5.53所示，其工作过程为：起爆电雷管，雷管引爆施主装药，装药爆轰驱动飞片运动，飞片经过定位块内一定距离的飞行后，撞击在电磁速度传感器里闭合回路的前臂上，此过程会在闭合回路的两端产生相应的感生电动势，信号由示波器捕捉。

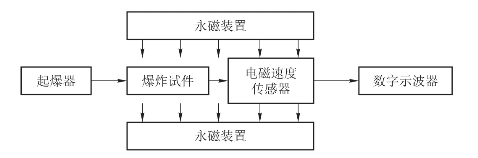
图5.53　电磁法测试飞片速度测试框图

为了保证电磁法测试施主装药爆炸驱动飞片平均速度的可靠性，对其中一种直径装药驱动飞片的速度采用VISAR（任意反射面激光干涉测速）法测试，利用该测试结果对电磁速度传感器进行标定。选用的装药：有机玻璃约束，装药直径为3 mm，装药高度为38 mm。选用的飞片：钛合金材质，厚度为0.1 mm。经过实验测试，电磁法得到的速度最大值比VISAR法要低11.24%，则速度最大值vm为

式中，xv为电磁法测得的飞片最大速度，经实验得出，两种方法测得的飞片平均速度偏差在7.2%以内，电磁法测得的最大速度比VISAR法低11.24%，因此，采用电磁法测试施主装药爆炸驱动飞片的最大速度需用式（5-114）修正，修正后的测试结果是可靠的。

3. 测试条件及测试结果

实验所用传爆药为JO-9C（Ⅲ）型细颗粒传爆药，药剂造型粉粒度为40～100目，装药约束套筒材料为有机玻璃，套筒外径为20 mm，药筒高度为38 mm，装药内径为1.5 mm、3 mm和5 mm。装药密度为（1.707±0.005）g/cm3（90%理论密度），为保证压药密度并避免密度梯度，采用定位压药的方法分多次将施主装药压制成型。飞片分为5种，列于表5.19中。

表5.19　飞片的具体参数[12]

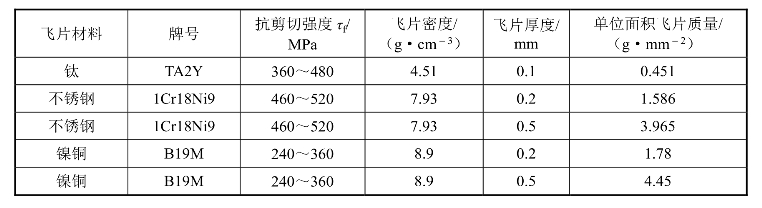
利用电磁法对不同直径施主装药驱动不同飞片进行测试，每个实验条件下测试3个有效数据。利用分析软件将实验结果拟合得到了相应的飞片速度规律曲线，如图5.54～图5.56所示。

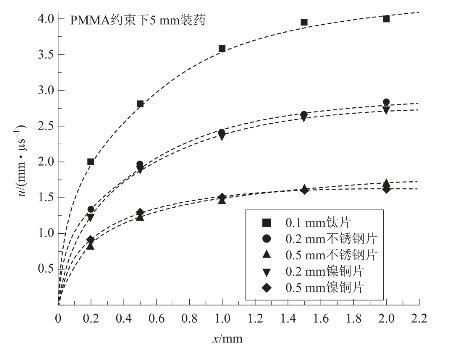
图5.54　5 mm装药驱动不同飞片的平均速度规律

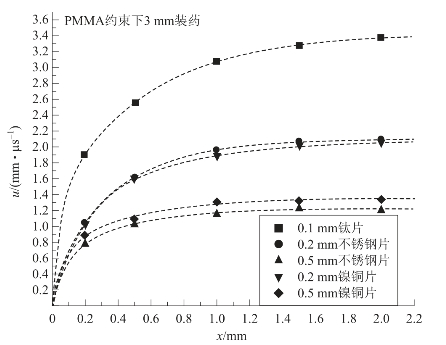
图5.55　3 mm装药驱动不同飞片的平均速度规律

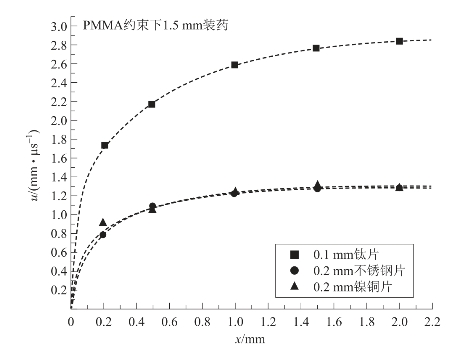
图5.56　1.5 mm装药驱动不同飞片的平均速度规律

飞片速度随飞行距离变化的实验规律数学表达可以用统一的形式：

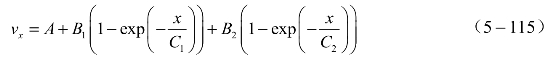
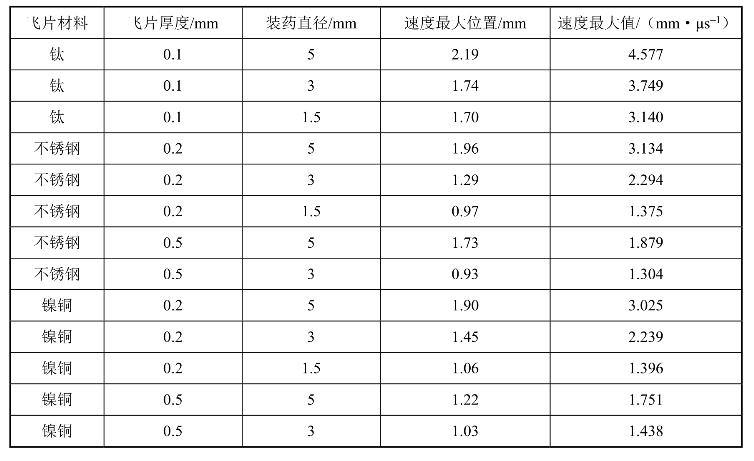
式中，vx为飞行距离x的飞片速度；A、B1、B2、C1、C2均为拟合系数，根据不同的实验条件、装药直径、飞片材料可得到不同的拟合系数。利用数据处理方法可以得到施主装药驱动不同飞片的速度最大值位置及相应的速度最大值，见表5.20。

表5.20　不同装药驱动不同飞片的速度最大值位置

5.2.3.4 飞片起爆能量传递规律

飞片起爆是以施主装药驱动的高速飞片为能量载体撞击受主装药，在受主装药中产生冲击波使之起爆，因此施主装药驱动能量传递问题包括飞片最大速度求解、飞片最大速度出现的位置和飞片撞击受主装药的能量产生问题。

1. 格尼（Gurney）方程

炸药驱动飞片运动的速度理论计算方法有以下几种：Gurney提出的Gurney模型、Aziz提出的爆轰流体动力学模型、Yadav建立的数学模型、谢兴华的一维爆炸流场模型、耿俊峰的径向流场模型和张厚生的炸药示性值计算方法。因为Gurney方程应用的范围最广，本章主要介绍Gurney模型。

Gurney方程是计算炸药驱动飞片最大速度的常用方法，该方程根据动量守恒定律和能量守恒定律，并采用了几点假设：① 炸药爆轰过程符合瞬时爆轰理论，不考虑冲击波在飞片和产物间的反射和透射；② 爆轰产物的密度为恒定值，且速度随距离呈一维线性分布；③ 炸药的能量全部转换为金属和爆轰产物的动能。Gurney方程针对对称装药结构和不对称装药结构分为以下几种情况进行求解：

对称装药结构分为三种情况，如图5.57～图5.59所示。

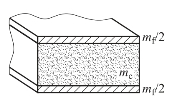
图5.57　对称平板约束装药

图5.58　圆筒内的圆柱装药

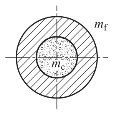
图5.59　球壳内的球形装药

（1） 对称平板约束装药：

（2） 圆筒内的圆柱装药：

（3） 球壳内的球形装药：

(www.xing528.com)

不对称装药结构分为两种情况，如图5.60和图5.61所示。

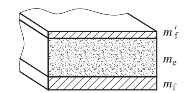
图5.60　不对称平板约束装药

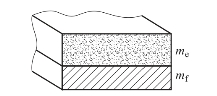
图5.61　不对称约束半开口装药

（1） 不对称平板约束装药：

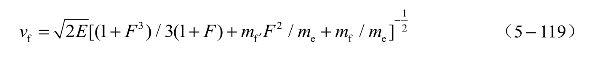
（2） 不对称约束半开口装药：

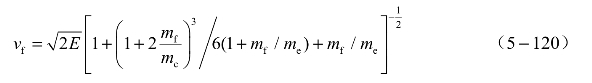
式中，vf为金属飞片末速度，即最大速度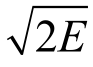；为炸药的Gurney特征速度，E为Gurney能，是指单位质量炸药爆炸后释放的热能中转换为气体爆轰产物和金属飞片运动的能量；mf、fm′分别为金属飞片质量；me为炸药质量；符号F=(1+2mf/mc)/(1+2mf/mc)。

对于不同结构的装药形式，可以采用不同形式的Gurney方程计算炸药驱动飞片的最大速度，但Gurney方程的模型均为驱动侧向飞片，且未考虑装药尺寸的影响。

2. 飞片最大速度计算方法

如图5.62所示，施主装药爆轰驱动飞片加速，飞片经过一段飞行距离后高速撞击受主装药，在受主装药中产生冲击波将其起爆。在此选用Gurney方程的半开口结构，其主要假设为：① 爆轰反应瞬间完成，不考虑冲击波在飞片表面的反射，认为飞片在瞬间被加速到了最大速度vf；② 爆轰产物的密度是各向均匀的，其速度分布为其拉格朗日位置的线性函数；③ 炸药的能量全部转换为金属飞片和爆轰产物的动能。

基于以上假设建立的炸药驱动飞片坐标系如图5.63所示。对于图5.63中的模型，取装药和飞片为研究对象。根据能量守恒定律：

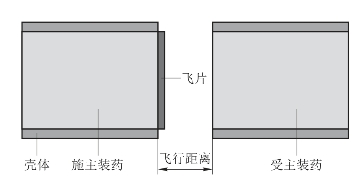
图5.62　施主装药驱动飞片撞击受主装药

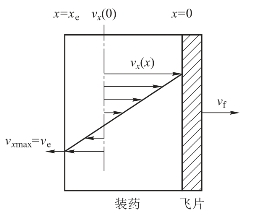
图5.63　施主装药驱动飞片坐标系

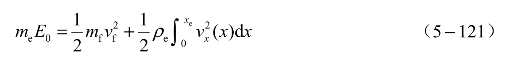
对式（5-121）积分后可得

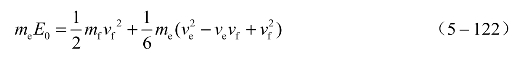
根据动量守恒定律：

积分后可得

式中，vx (x)=(ve+vf)x/xe-vf；mf为单位面积飞片的质量；me为单位面积炸药的质量；vf为飞片的最大速度；ve为爆轰产物气体的最大速度；vx(x)为爆轰产物气体在x处的速度。

联立式（5-122）和式（5-124），可以得到

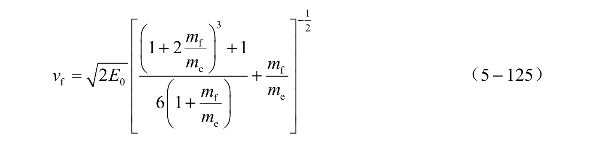
式中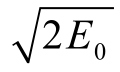，为炸药的Gurney特征速度。

有文献给出了Gurney特征速度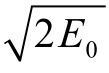的表达式：

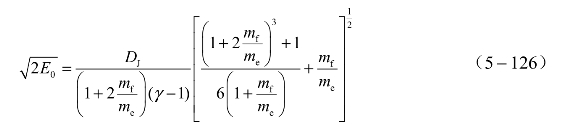
式中，DJ为装药的爆速；γ为爆轰产物的等熵指数。

将式（5-116）代入式（5-125），并用膨胀角模型理论的爆速Dj代替DJ，得到飞片速度的表达式：

3. 有效药量折算角的确定

利用式（5-122）进行计算时，由于一般情况下施主装药较长，装药长度远大于装药直径，并非所有装药量对驱动飞片加速都有贡献，在此，me采用有效药量的计算方法。

如图5.64所示，施主装药爆炸时，爆轰产物径向膨胀而产生稀疏波，稀疏波经过的区域即图中施主装药边缘沿径向的eα角包含的装药对驱动飞片没有贡献，对于装药高度大于装药直径的情况，实际上对驱动飞片有贡献的是以施主装药直径为底的圆锥形装药，该圆锥形装药即有效药量。当装药直径小于装药长度的无约束药柱爆轰时，有效药量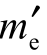计算公式[13]为

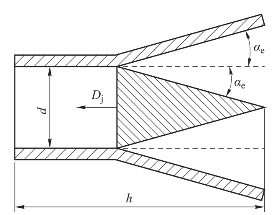
图5.64　有效药量计算模型示意图

式中，d为装药直径；αe为无约束装药的折算角。

由于式（5-128）的适用条件是无约束药柱，而施主装药的约束条件很强，阻挡了径向稀疏波的侵入，显然折算角应小于无约束药柱。有文献假设有约束装药和无约束装药的折算角之比与径向产物的飞散速度之比呈线性关系，最终给出了有约束装药折算角的计算公式：

式中，θ为无约束装药的折算角；Wm为单位长度外壳的质量；We为单位长度装药的质量。

利用式（5-128）和式（5-129）计算有效药量后代入式（5-127）中，计算得到的飞片最大速度以及与实验值的对比，经实验数据对比发现利用式（5-129）得到的折算角θ计算飞片速度与实验值的偏差较大。直接利用实验得到的飞片速度值代入式（5-127）和式（5-128）来反推有约束微装药的折算角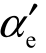，得≈12.45°。

为了验证其合理性，将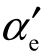≈12.45°代入式（5-128）和式（5-127），将得到的飞片速度计算结果同实验结果相对比，计算结果与实验结果基本符合，所有条件下的偏差均在15%以内，说明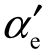≈12.45°对于工程计算有约束施主装药驱动飞片的最大速度是一个很好的近似。

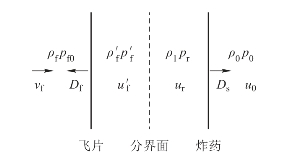
图5.65　飞片撞击受主炸药后的界面波系图

4. 飞片冲击受主炸药产生的能量计算

当飞片高速撞击炸药时，由于金属飞片的冲击阻抗大于炸药的冲击阻抗，因此飞片与炸药的界面产生一道向炸药传播的冲击波，并同时向飞片反射一道冲击波，界面波系图如图5.65所示。

根据动量守恒定律：

对于炸药：

对于飞片：

由飞片和炸药的冲击压缩规律：

对于炸药：

对于飞片：

由界面连续条件：

联立式（5-130）～式（5-135），可得

式中，。

将ur代入式（5-133）和式（5-130）即可得到Df和pr。

飞片作用时间：

式中，lf为飞片厚度。

飞片撞击炸药产生的能量EC为

常用炸药的临界起爆能量经查表可获得。