弯曲装药的设计与爆速计算：利用平衡条件解决平面力系问题

弯曲装药是指在传爆路径上存在弯曲的装药。当装药的曲率半径小于某值时，弯曲装药的爆速小于直线装药的爆速，并且爆速亏损与装药曲率半径之间存在着一定的关系。

5.1.3.1 小尺寸弯曲装药爆速亏损现象物理模型与数学方程

弯曲装药的爆轰波传播，其传播方向根据装药边界或装药形状时刻在变化，其实质仍属于爆轰波的绕射问题。因此对于圆弧装药的稳定爆轰，可抽象为爆轰波的连续拐角绕射，圆弧装药爆轰波传播的物理模型如图5.17所示。其中，假设爆轰波在单位时间Δt内传播单位弧长Δs由a到达b位置，相当于通过小装药拐角Δθ=Δs/R ，R为装药的曲率半径。由拐角效应现象可知，爆轰波通过装药拐角，拐角扰动使拐角附近的爆速低于该尺寸下的直线爆速。所以，圆弧装药的爆速低于直线装药的爆速，圆弧装药相对于直线装药存在爆速亏损现象[54,55,111,112]。

根据以上分析，可以利用拐角装药爆轰延迟时间的理论，将弯曲装药爆轰波传播问题转换为爆轰波沿拐角传播的问题，从而从理论上解决弯曲装药爆速亏损的计算。理论分析中，假定爆轰波由A向B传播，其传播示意图如图5.18所示，曲率半径为R。

图5.17　弯曲装药爆轰波传播物理模型

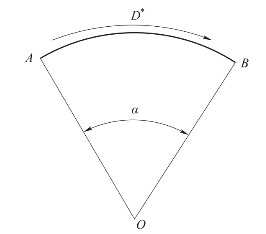
图5.18　爆轰波沿弧线传播示意图

设圆弧装药爆速为D*，直线爆速为D，则如图5.18所示，爆轰波沿由A向B传播时，在︵AB间的传播时间为

将AB分为N份，每份弧长用弦长取代，则爆轰波沿弦传播时间为

式中，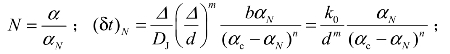

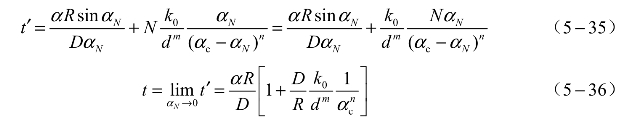
考察式（5-36）可知，如果不满足极限条件“收敛”，极限将不存在，亦即小拐角的爆轰传播时间不存在。这当然是不符合实际的荒谬结论。因此，极限条件“收敛”必定成立。

若用DΔ表示相同装药尺寸下直线爆速与弯曲装药爆速之差，则D-DΔ为该装药尺寸下弯曲装药的平均爆速，可得

联立式（5-36）与式（5-37）可得

经泰勒级数展开并剔除高阶项，得

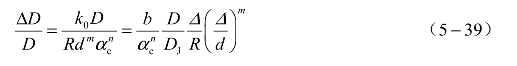
令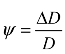为爆速亏损，上式即爆速亏损的数学表达式，该式表明，爆速亏损ψ与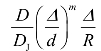成比例，其中是爆轰反应区尺度与沟槽尺度之比，是爆轰反应区尺度与圆弧曲率半径之比，是尺度d直线沟槽装药的爆速与C-J爆速之比。

上式可进一步简化为

根据拐角延迟时间的研究结果，式（5-40）中m=0.6。比例系数为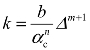，该系数可通过测定不同曲率条件下的爆速，并对测试结果进行线性回归而得到。该式的物理意义为：ψ与R成反比；当R→∞时，ψ=0，*D=D，为直线爆轰；当R→0时，ψ→∞，D*→0，理论上不能传爆。

5.1.3.2 小尺寸弯曲装药爆速亏损的试验研究

理论研究表明，炸药性质不同、约束材料及约束条件不同，爆轰延迟时间不同，其爆速亏损也应不同，因此在研究中选定炸药为HMX含量为96.00%～96.50%的超细化钝感HMX，HMX的平均粒径为587.3 nm。装药方法采用精密压装[11]，设计平均装药密度为1.77 g/cm3，基板材料选定为LZ12。为了分析所研究的传爆药在小尺寸条件下的爆速亏损现象及其变化规律，研究中分别设计加工了沟槽尺寸为0.6 mm × 0.6 mm、0.8 mm × 0.8 mm，弯曲曲率半径分别为5 mm、10 mm、15 mm、20 mm的试验基板，基板平均装药密度为1.77 g/cm3，基板装药效果如图5.19所示。

图5.19　不同曲率半径弯曲装药在同一网络基板上的压装效果

弯曲装药爆轰延迟时间测试原理与直线装药爆速测试原理相同，采用薄膜探针法测量。在小尺寸装药条件下，由于爆轰波阵面不是平面，而是弯曲的曲面，如图5.11所示。图中d是装药尺寸，R是爆轰波阵面的曲率半径，a为距轴线X处的夹角，D为轴线爆速，DX为距轴线X处的爆速。从图5.20可以看出，装药尺寸越小，爆轰波阵面的曲率半径将越小，距离轴线X处爆速DX与轴线上的爆速D偏差也将越大。

按爆轰稳定传播的条件，由几何关系可得出

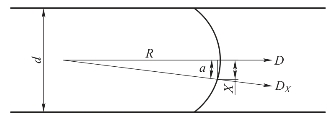
图5.20　小尺寸装药弯曲波阵面示意图

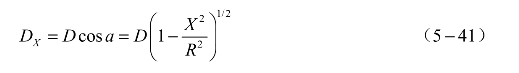
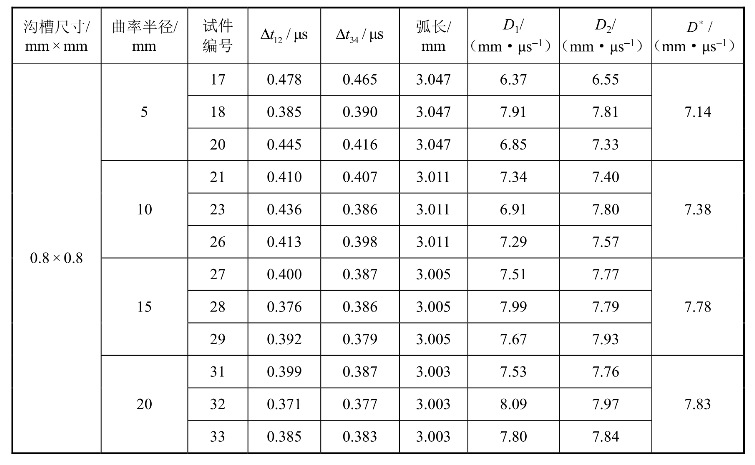
在进行小尺寸装药爆速测定时，传感器的安装将对测试精度产生影响，应将薄膜探针安装在沟槽的中心位置。在每个测试件的沟槽中安装两个薄膜电极传感器，每个传感器包含两对电极，图5.21（a）中1、2、3、4分别表示四对电极的切口，同一传感器上两对电极切口中心的直线距离为3 mm，利用测试仪器记录爆轰波通过各个切口的时刻，可获得两组对电极导通的时间差Δt12、Δt34，通过该时间差及两传感器间的弧线距离l可计算爆速。传感器安装后的测试件如图5.21（b）所示，弯曲装药爆速计算结果如表5.7所示。(www.xing528.com)

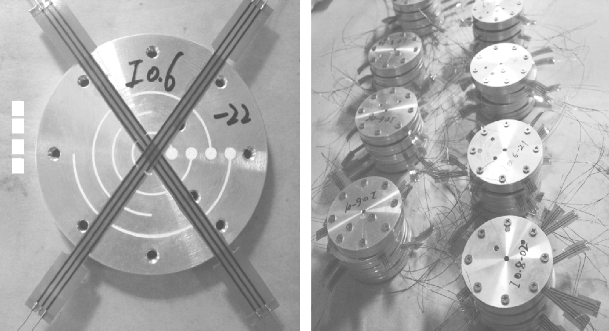
图5.21　弯曲装药爆速亏损测试件

（a）薄膜电极安装图；（b）测试件封装图

表5.7　设计平均装药密度为1.77 g/cm3时弯曲装药爆速计算结果

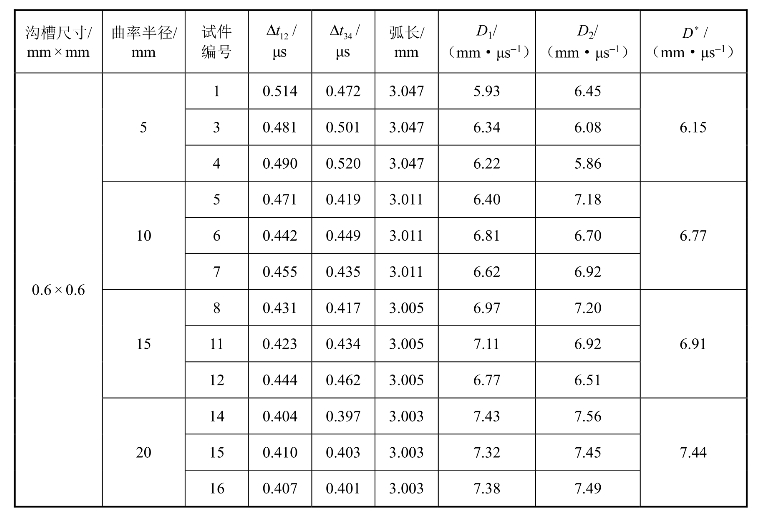
表5.7中，D1为测试点1、2间爆轰波沿弧线传播的平均速度；D2为测试点3、4间爆轰波沿弧线传播的平均速度。令D*为弯曲装药爆速，则D*=D-ΔD ，取同一装药尺寸同一曲率下多组测试件所得D1与D2的均值，结果如表5.7所示。在直线装药爆速与装药尺寸关系的研究中，得到在沟槽尺寸为0.6 mm × 0.6 mm时，该装药密度下直线装药的爆速为D=7.49mm/μs 。从表5.7的试验数据可以看出，各种曲率半径下所测爆速均小于直线装药爆速，说明在弯曲装药的条件下，确定存在着爆速亏损现象，装药尺寸相同时，曲率半径越小，爆速亏损越大。

根据爆速亏损的定义，对表5.7中的试验数据进行处理，得到装药尺寸为0.6 mm × 0.6 mm时，爆速亏损与装药曲率半径的关系，如表5.8所示。

表5.8　装药尺寸为0.6 mm × 0.6 mm时爆速亏损与装药曲率半径关系

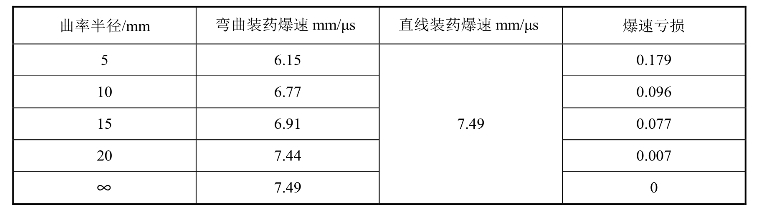
将D=7.49mm/μs ，DJ=8.56mm/μs ，m=0.6和d=0.6mm 代入式（5-40），并结合表5.8中的实验数据进行线性回归，得到k=0.753。爆速亏损的表达式为

分别将爆速亏损的测试数据与由式（5-42）得到的计算数据作图，就可以得到装药曲率半径的倒数与爆速亏损之间的关系，如图5.22所示。

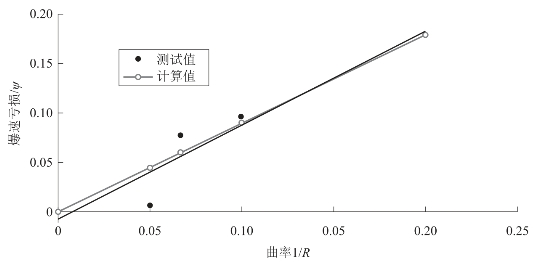
图5.22　装药尺寸为0.6 mm × 0.6 mm时爆速亏损与装药曲率之间的关系

从图5.22可以看出，计算结果和测试结果的变化趋势一致，两条曲线吻合较好。为了进一步验证理论推导的合理性，还设计加工了沟槽尺寸为0.8 mm × 0.8 mm，弯曲曲率半径分别为5 mm、10 mm、15 mm、20 mm的试验基板进行试验，采用同样的压装工艺对基板实施装药，平均装药密度为1.77 g/cm3。按前述测试方法测得不同曲率半径下的爆速，如表5.9所示。

表5.9　设计平均装药密度为1.77 g/cm3时弯曲装药爆速计算结果

根据爆速亏损的定义，对表5.9中的试验数据进行处理，得到装药尺寸为0.8 mm × 0.8 mm时，不同曲率半径下的爆速亏损，如表5.10所示。

表5.10　装药尺寸为0.8 mm × 0.8 mm时爆速亏损与装药曲率半径的关系

该尺寸下的直线爆速可由公式计算得D = 8.306 mm/μs，将D = 8.31 mm/μs，DJ =8.56 mm/μs，m = 0.6和d = 0.8 mm代入式（5-40），并结合表5.10中的实验数据进行线性回归，得到k′ = 0.734。爆速亏损的表达式为

分别将爆速亏损的测试数据与由式（5-43）得到的计算数据作图，就可以得到装药曲率半径的倒数与爆速亏损之间的关系，如图5.23所示。

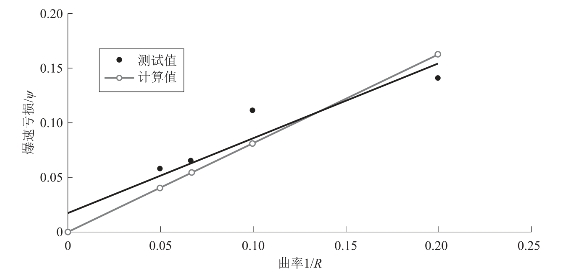
图5.23　装药尺寸为0.8 mm × 0.8 mm时爆速亏损与装药曲率之间的关系

对比图中的测试结果曲线和计算结果曲线可以看出，二者均为线性关系，且变化趋势基本相同。比较式（5-42）与式（5-43），待定系数分别为k=0.753，k′=0.734，其偏差约为2.5%。出现偏差的原因可能包括：① 测试误差；② 拟合的待定系数内含不确定的边界条件αc。如果进一步考察αc的影响，大沟槽的αc比小沟槽的αc大，那么，两式分母的差别会更小，即当把表达式（5-40）改为

则所得待定系数有可能更为接近。以上分析结果可以说明该两种装药尺寸下的爆速亏损均基本符合式（5-40），亦即理论推导是合理的。

利用公式计算不同尺寸下的直线爆速，并取k、k′的平均值作为式（5-40）的待定系数计算各装药尺寸下不同曲率半径所对应爆速亏损，计算结果如表5.11所示，相应曲线如图5.24所示。

表5.11　不同装药尺寸下爆速亏损与装药曲率半径的关系

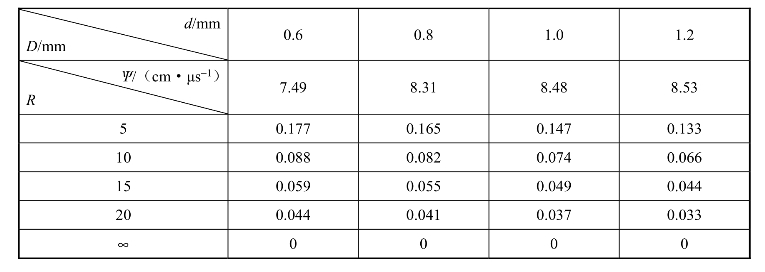
从图5.24可以看出，相同装药尺寸下的爆速亏损随曲率半径的增大而减小，相同曲率半径下的爆速亏损随装药尺寸的减小而增大，符合基本的物理规律，说明式（5-40）是一个比较理想的爆速亏损表达式。

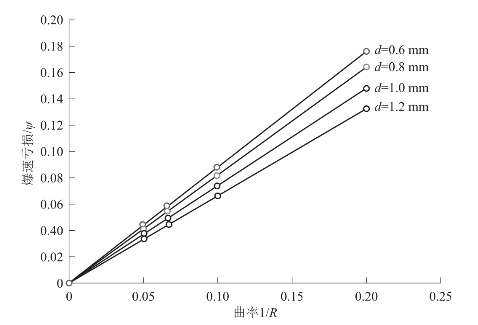
图5.24　不同装药尺寸下爆速亏损与装药曲率之间的关系