直线装药的装药直径对微装药爆压的影响

直线装药，是指炸药微装传爆路径为直线的装药。

5.1.1.1 小尺寸装药的直径效应

爆轰波在炸药中能稳定传播的原因在于化学反应能供给能量，维持爆轰波毫无衰减地传播下去。如果这个能量受到损失，爆轰波就会因缺乏能量而衰减。20世纪40年代，Khariton[1]首先量化地描述了直径效应对爆轰波速度和临界直径的影响。他利用从侧面侵入反应区的稀疏波引起的能量损失来解释直径效应，提出的定律可以表示为

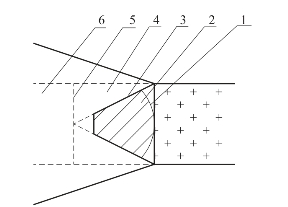
图5.1　有限尺寸装药爆轰波阵面示意图

1—弯曲波阵面；2—未受膨胀波影响的反应区；3—径向稀疏波阵面；4—受膨胀波影响的反应区；5—C-J面；6—爆轰反应产物

式中，C为爆轰产物中的平均声速；τ为爆轰反应区内的化学反应时间。

对于dc＜d＜dL（dc为临界直径，dL为极限直径）的有限尺寸装药，爆炸化学反应及爆轰波阵面如图5.1所示。图中，对截面为圆形的沟槽，则d为装药直径；对截面为正方形的沟槽，d为沟槽的边长。

假设爆轰波反应区内完成化学反应所需的时间为t1，膨胀波从装药侧面到达轴线的时间为t2，如图5.1中2区的虚线所示，此时t1＞t2，反应区化学反应还未完，膨胀波已经到达轴线处，结果使得反应区支持爆轰波的有效能量减少，整个波阵面的爆速低于极限爆速。装药尺寸越小，反应区受膨胀波影响区域就越大，爆速就越低，当装药尺寸小于dc时，爆轰将熄灭，这种现象就称为小尺寸装药的直径效应，dc称为小尺寸装药的临界尺寸。同理，当装药尺寸d≥dL时，爆轰波反应区内完成化学反应所需的时间t1小于膨胀波从装药侧面到达轴线的时间t2，此时爆轰波反应区内的化学反应能提供足够的能量支持爆轰波，使爆轰波以恒定的速度传播，dL就称为小尺寸装药的极限尺寸。

1949年，Eyring[2]通过对小直径装药爆轰波阵面的曲率进行研究，提出了爆速直径效应的流体力学理论模型，通过理论推导并结合大量的实验数据得到了直径效应的半经验公式，把爆速亏损（即有限直径的药柱中定态爆速相对于理想爆速的减少量）同爆轰反应区厚度a联系起来。

无外壳装药时：

有限厚度外壳装药时：

无限厚度外壳装药时：

式中，Wc和We分别为外壳和装药的质量；φ为药柱边部爆轰波阵面法向与侧面的夹角。事实上，在Eyring公式中a的作用是一个经验参数，或者反过来从直径效应的实验数据可以给出关于a的估计。

5.1.1.2 流管理论

为了减弱侧向稀疏波对微装药爆轰波传播的影响，微装药多为带壳装药。图5.2（a）所示为带壳微装药爆轰波传播原理示意图。爆轰波以稳定爆速Dj传播，受到侧向稀疏波的影响，反应区能量对前沿冲击波的支持比理想爆轰弱，前沿冲击波和反应结束面呈曲面，是典型的二维定常爆轰波传播问题。

图5.2 带壳微装药爆轰波传播原理示意图

（a）带壳微装药爆轰波传播示意图；（b）准一维定常爆轰传播模型示意图

1—微小尺度装药；2—壳体；3—爆轰波前沿；4—反应区；5—反应结束面；6—爆轰产物

Jones[3]的流管理论将爆轰波阵面的弯曲转化为爆轰反应区的扩张（图5.1中为了标注方便，并未按比例画出），作出了以下假设：① 将曲线爆轰波近似为平面爆轰波；② 化学反应结束面Aj也是爆轰产物的声速面；③ 在反应区内，A的变化只与横坐标x有关；④ 在A0与Aj之间的任何截面上，物理量不随径向改变。

以上假设将二维定常爆轰问题简化为一维定常爆轰问题。在相对于爆轰波的静止坐标内，爆轰波的流动示意图见图5.2（b）。

令e分别表示介质内能，A表示流管的截面积，下标0表示炸药区状态，s表示前沿冲击波后的状态，j表示反应结束状态，Dj表示微装药非理想爆轰的爆速，DJ表示不考虑直径效应的理想爆速。

得到的Dj与DJ的关系式为[4]

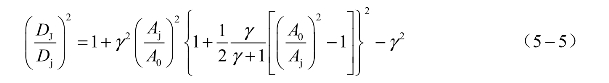
由于A0=πr2，Aj=π(Δtanφ+r )2，则

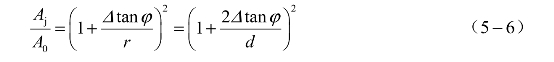
式中，r为装药半径；d为装药直径；Δ为反应区厚度；φ为反应区内爆轰产物膨胀角。

5.1.1.3 爆速-直径变化关系

令β = ctanφ为约束强度，η = Δ/d为反应区相对厚度，则有

代入式（5-6）有

将式（5-8）代入式（5-5），化简得到

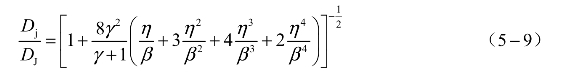
当η/β≪1时，在η/β零点处进行两次泰勒级数展开，取一阶项得

由图5.3可知，约束强度的倒数1/β的表达式为

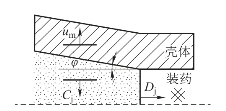
式中，um为装药与壳体界面处的粒子速度。

(www.xing528.com)

图5.3　微装药壳体受压侧向膨胀示意图

微装药的外壳受压膨胀初期，在反应区内的高压作用下，界面产生向壳体径向传播的冲击波，同时沿径向向反应区发出一簇径向稀疏波。

假设：① 反应区内的状态近似为反应结束面的状态；② 反应区内压力对壳体的高压作用近似为正冲击作用；③ 将反射稀疏波簇近似看成一道弱冲击波。

根据动量守恒定律有

壳体冲击波：

对爆轰产物：

界面连续条件：

式中，pr为界面处爆轰产物的压力；ur为产物径向膨胀速度；Cj为壳体向反应区反射的弱冲击波速度；ρm0为壳体材料的初始密度。

联立式（5-12）、式（5-13）和式（5-14），得到

令，则有

得到

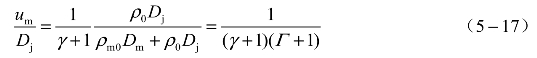
式中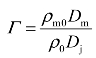，为约束材料与炸药冲击阻抗比。

因此，

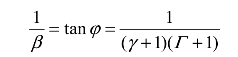
将式（5-18）代入式（5-10）得

令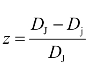表示微装药爆速的直线亏损，则有

图5.4所示为Dj-d曲线图。当装药直径增加时，爆速逐渐接近DJ，即接近理想爆轰的爆速。在实际应用中，取Dj = （98%～99%）DJ为极限爆速，对应的直径为极限直径dL。式（5-16）中的Dj取为临界爆速Dc时，对应的装药直径即临界直径dc，假设Dc = ζDJ，显然，无量纲量ζ的取值应在0～1。

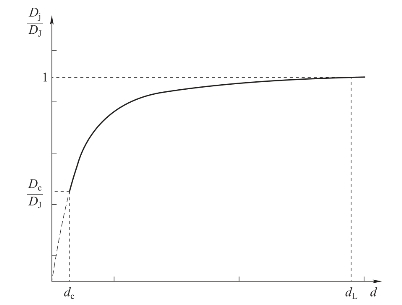
图5.4　Dj-d曲线图

5.1.1.4 爆压-直径变化关系

理想爆轰参数pJ与DJ之间存在关系：

对于微装药爆压pj的理论计算公式，假设pj、Dj与pJ、DJ之间满足如下关系：

式中，m和n均为与Γ有关的无量纲量。

将式（5-20）中Dj的数学表达式代入式（5-22）中可得

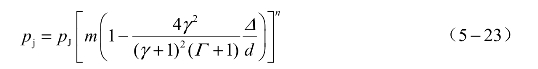
从式（5-23）的表达形式可以看出，在刚性约束下，即Γ为无穷大时，微装药的爆轰应为理想爆轰，此时m和n应分别等于1和2，因此可以假设m和n有如下数学表达形式：

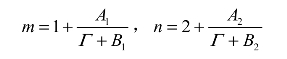
式中，A1、B1、A2和B2为待定系数，均为量纲为1的量。实验数据回归可得

A1 = 0.135，B1 = 1.75；A2 =-7.5，B2 =-4.25

此计算公式的适用条件：0≤Γ＜3.25；当计算结果pj＞pJ时，取pj = pJ。

图5.5为利用式（5-19）得到的四种不同约束条件下微装药爆压随装药直径的变化规律。四条曲线的约束条件从左至右分别为：45钢约束、铝约束、有机玻璃约束和无约束。从图中可以看出，在相同装药直径下，微装药的爆压随着约束强度的增大而增大，说明计算微装药爆压的式（5-19）不仅能够反映装药直径对爆压的影响，也能反映约束条件对爆压的影响。

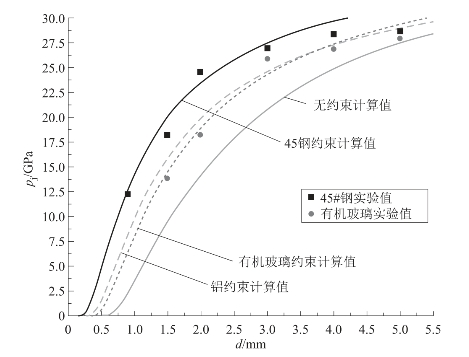
图5.5　四种不同约束条件下的微装药爆压随装药直径的变化规律