一维流体力学模型探究

流体力学模拟方法可以给出更详细的飞片飞行信息以及桥箔与飞片相互作用的机理，梁龙河和胡晓棉在此方面做了大量的工作[18,19]。对于一维流体力学模型的研究已经比较成熟，将流体力学模型应用到电爆等离子体驱动飞片工程的模拟中，关键是要解决桥箔爆炸后能量转化问题，即使飞片速度模拟结果不再完全依赖于实验数据。

4.4.2.1 流体力学模型的建立

桥箔爆炸形成的高温高压气体推动飞片，在加速膛的约束下，飞片中心部分在微秒量级的加速时间内可以考虑成一维运动。模型假设如下：① 爆炸箔从电路中吸取能量，在箔的薄层空间中可近似认为按质量均匀分布，仅随时间t而变化；② 背板质量远大于桥箔飞片质量；③ 飞片在高压气体作用下可忽略其强度，在短暂加速的快运动过程中，可忽略热传导及二维旁侧效应，认为呈理想流体状态，作一维平面不定常可压流运动。可以看出，上述假定条件前两项与经验模型是相同的，所不同的是爆炸蒸气密度在各点位置是不同的，飞片作一维平面不定常可压流运动。

根据上述假定对所述问题可采用拉氏一维平面不定常可压缩流体力学方程组描述：质量守恒方程：

动量守恒方程：

能量守恒方程：

运动方程：

电能方程：

状态方程：

式中，p、V、e、q、u和x分别为压力、体积、总能量、人为黏性、速度、位置；γ 为绝热指数；C0为声速。当电功率PP（t）给定后，上述6个方程能封闭求解6个未知量。电功率PP（t）由桥箔爆发电流和电压的模拟曲线得到。

在一维非定常流体力学方程中的功率PP的单位是MW/mg。爆炸箔吸收的电能并不能完全转化为飞片的动能，很大一部分能量通过光辐射等耗散掉。因此在根据上述基本方程计算飞片速度之前，必须对桥箔吸收的能量进行修正，也是说只考虑有多少能量用于驱动飞片。为简化复杂过程，采取转换的公式如下：

式中，mb和mf分别为箔桥质量和飞片质量；β 为转换系数，在一定实验参数范围内，它可以近似为常数，可由实验来确定。由此，用此模型不但可以计算出整个飞片速度随时间的变化曲线，还可以根据不同的边界条件组合计算出飞片内外边界网格中速度随时间的变化情况。另外，飞片层中的内能、压力和密度在不同时刻随网格的分布也可以很好地表示出。所以此模型描述的结果更加接近实际情况。利用差分方法可以求解上述方程组。

4.4.2.2 飞片速度的实验与数值模拟结果

采用上述一维非定常可压缩流体力学模型对文献［20］中所提供的实验结果进行模拟。图4.35～图4.38模拟速度分别对应表4.26和表4.27所示参数。

表4.26　电路参数

表4.27　雷管参数

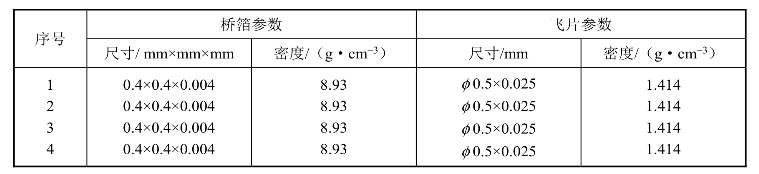
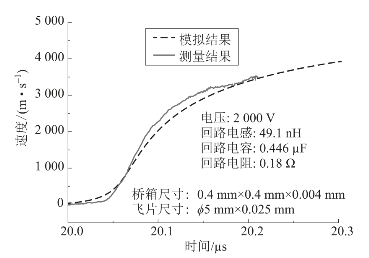
图4.35　飞片速度测量与模拟结果

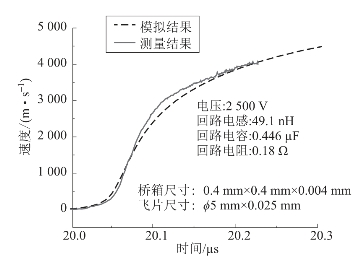
图4.36　飞片速度测量与模拟结果

图4.39是图4.35实验条件下，飞片飞行时间与飞行距离的模拟结果，从两个图的对比可以看出，实验测试飞片飞行距离约0.4 mm，在这个区间内，飞片速度实验结果略大于模拟结果，相对趋势基本是一致的。

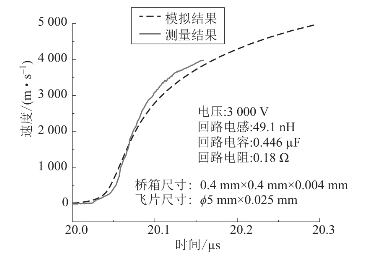
图4.37　飞片速度测量与模拟结果(www.xing528.com)

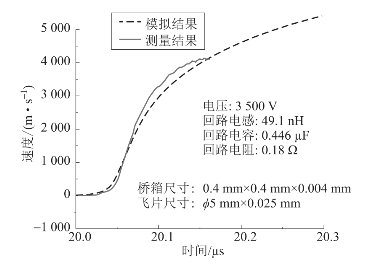
图4.38　飞片速度测量与模拟结果

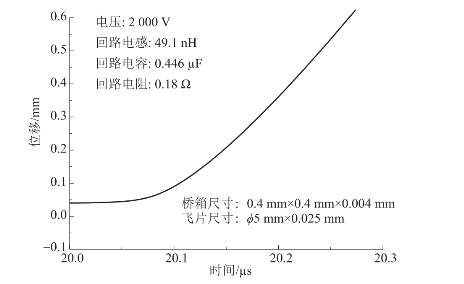
图4.39　飞片位移曲线

图4.40～图4.44是对应表4.28和表4.29 4种参数情况下的试验和模拟结果。

表4.28　回路电参数

表4.29　雷管参数

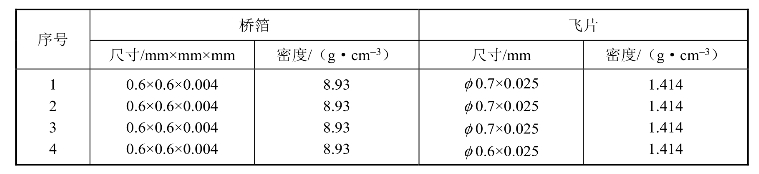
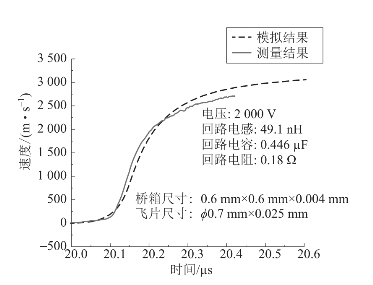
图4.40　飞片速度测量与模拟结果

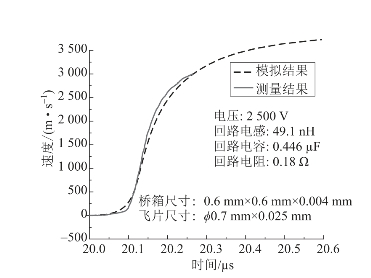
图4.41　飞片速度测量与模拟结果

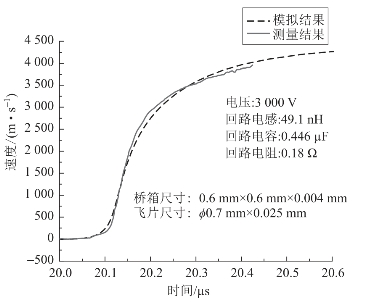
图4.42　飞片速度测量与模拟结果

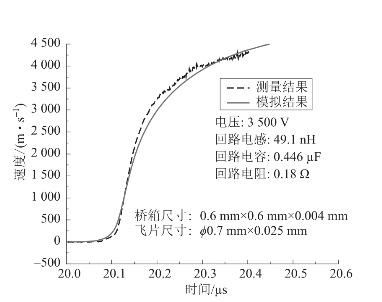
图4.43　飞片速度测量与模拟结果

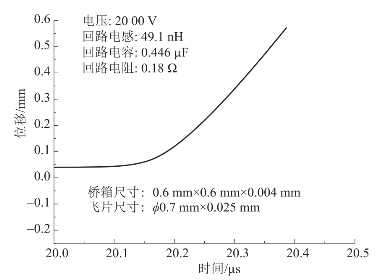
图4.44　飞片位移曲线

从上面的模拟结果看，飞片速度模拟的结果也与测量结果基本吻合。需要进一步改进的是飞片前期驱动模型。

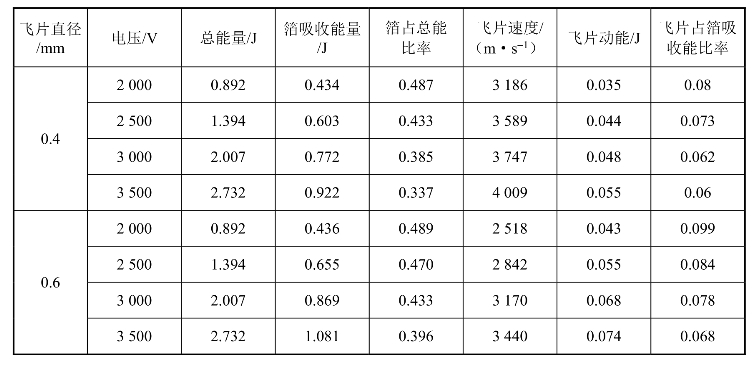
在飞片飞行0.3 mm处飞片速度与电压呈直线关系，如图4.45所示，这与文献值是一致的。在同样电路和桥箔参数下，随着飞片质量的增加，飞片速度也明显下降。表4.30是能量转换效率的情况，从表中可以看出随着电压的升高，桥箔吸收的能量增大，飞片吸收的能量也增大，但能量利用率降低。尽管如此，如果电容耐压允许，应该尽可能提高电压，以增大飞片速度。

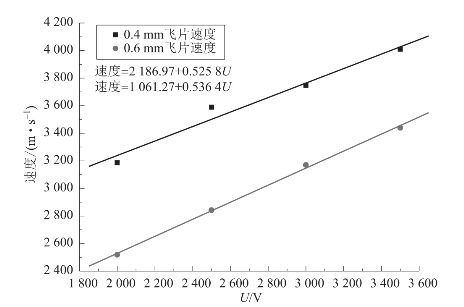
图4.45　飞片速度与电压的关系

表4.30　能量转换关系

4.4.2.3 数值模拟结果

对爆炸箔冲击片换能元和发火药柱装配成的发火组件进行数值模拟计算。图4.46为片速度，表4.31为实验参数。从图中可以看出，飞片速度可以达到2 500 m/s以上。

表4.31　回路电参数与桥箔、飞片参数

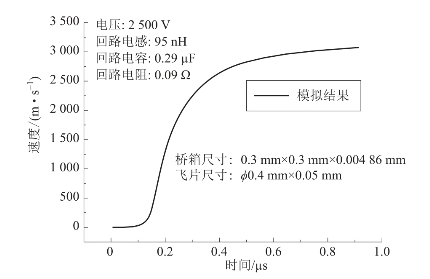
图4.46　飞片速度曲线

通过上面模型的介绍和分析，可以得到这样的结论，即对于一定桥箔尺寸范围内，可以利用电格尼能方法进行飞片速度的预估。对考虑飞片飞行的详细时间历程可以采用流体力学方法。流体力学模拟结果与实验结果具有很好的一致性，数值模拟结果和实验结果表明，在其他条件不变的情况下，飞片速度与充电电压成正比。飞片动能约占总能量的3%。