SCB电火工品的能量加载方式主要有恒流激励和电容放电两种,在恒流激励下SCB的发火方式为电热发火方式(发火件的发火是由于发火药剂达到发火温度而引起的),而在电容放电激励下SCB的发火方式有两种:电热发火和电爆发火(电爆发火是由于SCB的爆发而引起发火件的发火,它也分为两种,一种是SCB爆发产生等离子体,称为等离子体发火;另一种是SCB爆发但是没有产生等离子体,称为电爆发火)。本节针对SCB发火件在恒流激励和电容放电这两种常见情况下的发火模型进行介绍。
4.3.1.1 恒流激励下SCB发火件的发火模型
1. 模型假设
SCB的结构如图4.18所示,由于SCB相对于药剂和塞子而言非常小,所以可以将SCB看作一个热点,而将药剂和塞子看成两个半球体,其中药剂半球的半径取与塞子的半径相等,如图4.19所示。为了使模型简化,需作如下假设:① 忽略电桥和药剂,以及电桥和塞子接触面之间的接触热阻和热容,即交界面处三者的温度相等;② 忽略药剂的化学反应放热,即认为药剂为惰性物质;③ 电桥以均匀的热流密度向药剂和塞子传递热量,并且只存在热传导这一种传热方式,不考虑桥和药剂以及塞子之间辐射形式的散热;④ 假设SCB、药剂和塞子都是均匀且各向同性的物质,并且SCB和塞子的性质相同;⑤ 在整个过程中,桥、药剂和塞子的导热系数、密度、比热容等均不随时间变化。
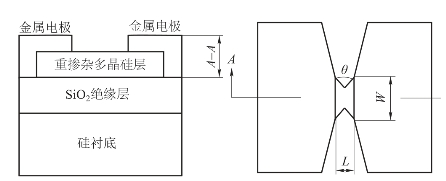
图4.18 SCB结构
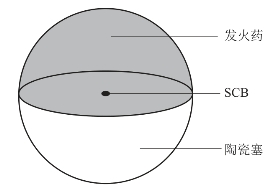
图4.19 SCB发火件简化模型
2. 数理模型
恒流激励时,电桥-药剂-塞子系统最终会进入稳定状态,所以由上述假设可知,电桥-药剂-塞子系统的传热问题可以归结为一维球体稳态导热问题,由于电桥-药剂半球和电桥-塞子半球是对称的,本章首先选择电桥-药剂半球为研究对象,这样电桥-药剂半球的传热方程与定解条件可表述如下:式中,r为药剂与桥片中心的距离(m);Te为药剂的温度(K);re∞为药剂的厚度(m);λe为药剂的导热系数(W/(m·K));he为药剂的表面散热系数(W/(m2·K));Ta为环境温度(K)。
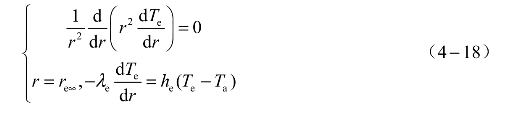
假设SCB的半径为r0,三者接触处的温度为Tm,那么由式(4-18)可得

将式(4-19)代入式(4-18),求得

同理可得塞子温度与Tm的关系为

单位时间内流过电桥-药剂半球的热量等于单位时间内电桥传递给药剂的热量,即
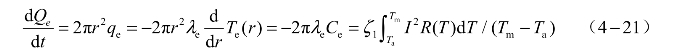
式中,ζ1为常数,它表示电桥传递给药剂的热量与电桥产生的热量的比值。
由式(4-21)可得
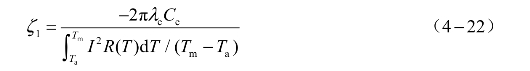
同理,单位时间内流过电桥-塞子的热量等于单位时间内电桥传递给塞子的热量,即

式中,ζ2为常数,它表示电桥传递给塞子的热量与电桥产生的热量的比值。
由式(4-23)可得
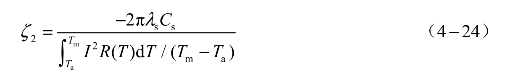
由于ζ1+ζ2=1,因此可以由式(4-22)和式(4-23)求得发火电流的表达式:
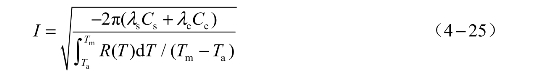
由式(4-19)和式(4-20)可以求得距电桥中心r处的药剂温度与电桥表面温度的关系为
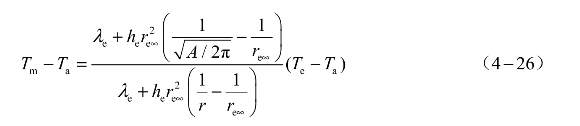
文献[10]中恒流激励下SCB发火件发火条件的定义为:距离电桥中心一倍的药剂粒径处的药剂温度达到药剂的发火点时,药剂发火。这个判据只适用于微型桥(MSCB),对于标准桥和较大的桥则不适用。为了将上述公式扩展到标准桥和大桥,本章对恒流激励下的发火条件做如下定义:对于微型桥,定义临界发火电流为恒流激励5 min能使距电桥中心2r0处的药剂温度达到发火点时的电流;对于标准桥和较大的半导体桥,则定义为恒流激励5 min能使距电桥中心5r0处的药剂温度达到发火点时的电流。利用式(4-25)和式(4-26)可以求出恒流激励下SCB发火件的临界发火电流。(https://www.xing528.com)
4.3.1.2 电容放电激励下SCB发火件的发火模型
由于电容放电速度非常快,在数十微秒级,热量只能在药剂和塞子内部很小一部分区域内传递,所以在电容放电激励下,本章选取电桥及其上下同等面积的药剂和塞子为研究对象对其发火的数理模型进行研究,如图4.20所示。
1. 模型假设
为了使模型简化,需作如下假设:① 忽略电桥和药剂,以及电桥和塞子接触面之间的接触热阻和热容,即认为电桥-药剂-塞子交界面处三者的温度相等;② 忽略药剂的化学反应放热,即认为药剂为惰性物质,系统内没有内热源;③ 只考虑热传导这一种传热方式,不考虑电桥和药剂以及塞子之间对流、辐射形式的散热;④ 在整个电容放电过程中,电桥、药剂和塞子的物化参数等均不随时间变化。
2. 数理模型
由上述假设可以将药剂的导热归结为一维平板无内热源非稳态导热问题,且具有第二类边界条件。以电桥的中心为坐标原点,垂直于SCB与药剂接触面的方向为x轴建立直角坐标系,如图4.21所示。由于电桥-药剂系统和电桥-塞子系统是对称的,本章首先选择药剂-电桥系统为研究对象,则药剂的导热微分方程和定解条件可描述为
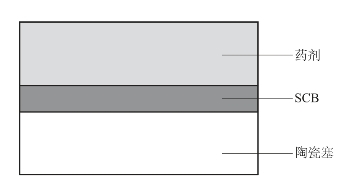
图4.20 SCB发火件模型
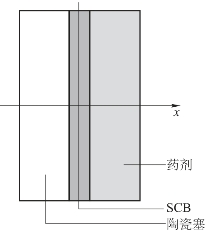
图4.21 SCB发火件坐标

式中,ke为药剂的热扩散率,ke=λe/ρece ,ρe为药剂密度(kg/m3);λe为药剂导热系数(W/(m·K));ce为药剂的比热容(J/(kg·K));qe为药剂与MSCB交界面处的热流密度;Ta为环境温度(K)。
根据塞子和药剂的对称性,塞子的导热微分方程和定解条件为
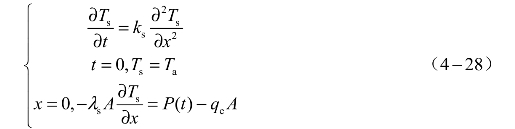
式中,ks为塞子的热扩散率,ks=λs/ρscs ,ρs为塞子密度(kg/m3);λs为塞子导热系数(W/(m·K));cs为塞子的比热容(J/(kg·K))。电容放电激励时,![]() ,U为激励电压(V);R为作用过程中SCB的平均电阻(Ω);C为放电电容(F),其余同式(4-27)。
,U为激励电压(V);R为作用过程中SCB的平均电阻(Ω);C为放电电容(F),其余同式(4-27)。
解上述方程可以得到距桥面任一距离x处药剂温度随时间变化的方程[10]:
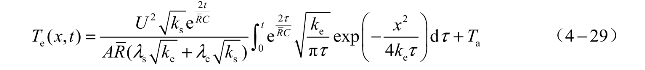
通过实验现象分析可知,在电容放电激励模式下存在两种发火方式:电热发火和电爆发火。文献[10]对这两种不同的发火方式下的临界发火电压采用不同的计算方法:
1)电热发火方式下临界发火电压的计算方法
电热发火时发火件的发火是由于距离桥片中心一定距离处的药剂达到发火点而引起的,这种情况下临界发火电压具体计算方法是:
(1)确定装药的发火层厚度,得到药剂爆炸延迟期与温度的关系。
(2)应用式(4-29)绘制某一激励电压V1下的Te(0,t)和Te(δ,t),并获得99%最高温度Te及对应的持续时间τe。
(3)判断药剂是否发火。
(4)若不能发生热爆炸,则取V2>V1,重新计算;若能发生热爆炸,但高温持续时间大于热爆炸延迟期,则取V3<V1,重新计算。
2)电爆发火方式下临界发火电压的计算方法
电爆发火时发火件的发火是由SCB的爆发引起的,这种情况下临界发火电压就是使桥爆发的电压,而桥爆发的判据为桥的最高温度达到其爆发点时认为桥爆发。由文献[10]知爆发点的计算公式可表述如下:
![]()
式中,Tmelt为硅的熔点1 684 K;Tg为多晶硅的沸点2 880 K;S0定义为SCB的有效面积,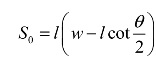 ,如图4.22所示。
,如图4.22所示。
由式(4-29)可以求得SCB的最高温度Tm,则电爆发火时SCB的临界发火电压的计算公式可表述如下:

图4.22 SCB有效爆发面积
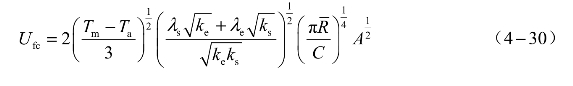
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




