发火组件的点火实验

为了验证上述发火模型的正确性，本章选择两种不同的金属桥带发火件分别进行5 min恒流激励实验和50 ms恒流激励实验。

4.2.2.1 5 min恒流激励实验

1. 实验条件

实验所用的换能元同3.2.2.1节，所用的药剂为KClO4/Zr，装药条件如表4.10所示。

表4.10　装药条件

2. 实验方法和结果

实验电路图和所用仪器设备同3.1.2.2节，另外由于要测发火时间，所以实验设备还包括一个光靶。按照D-最优化法测试出金属桥带发火件的50%发火电流和标准差，然后按照正态分布模型计算出安全电流和全发火电流，如表4.11所示。

表4.11　5 min恒流激励时金属桥带的临界发火电流实验结果

实验中观察到在各组实验中都存在发火件发火而桥带没有断的情况，如图4.12所示。这说明发火件的发火是由于桥带产生的焦耳热使药剂升温到发火点而引起的药剂发火，也就是说在5 min恒流激励情况下金属桥带发火件的发火方式属于电热发火。

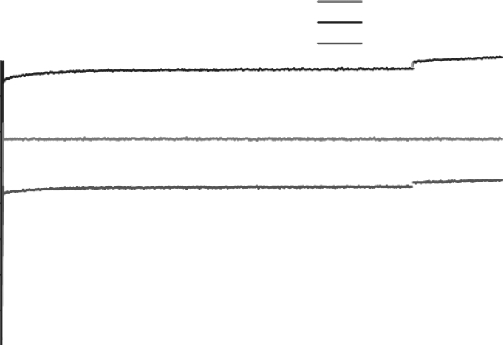
图4.12　2#样品/Zr/KClO4激励电流1.44 A药剂发火，而桥未断

3. 实验与理论对比

由实验现象的分析可知，在恒流激励情况下，发火件的发火方式属于电热发火方式，所以本书将金属桥带发火件恒流激励模式下的发火条件定义如下：紧贴桥带表面的一层药剂的温度达到药剂发火点时，发火件发火。按照上述定义和式（4-15）～式（4-17）的差分表达式，利用MATLAB软件就可以计算5 min恒流激励时的临界发火电流，将计算结果与实验结果进行对比，结果如表4.13所示（计算所用的药剂参数如表4.12所示）。

表4.12　药剂参数

表4.13　5 min恒流激励时桥带发火件的临界发火电流的理论计算值与实验值对比(www.xing528.com)

从表4.13可知，桥带发火件的临界发火电流的理论计算值与实验值的误差在10%以内，理论计算结果与实验值的一致性很好，所以上述模型和计算方法可以用来计算桥带发火件的临界发火电流。

4.2.2.2 50 ms恒流激励实验

1. 实验方法和结果

实验样品和方法同4.2.2.1节，实验所用设备同4.1.2.2节，实验结果如表4.14所示。

表4.14　50 ms恒流激励时金属桥带发火件临界发火电流实验结果

实验中发现当激励电流在临界电流附近时，发火件发火和桥断是同时的，如图4.13所示；当激励电流高于临界电流时，桥带断在先，而药剂发火在后，如图4.14所示。这说明在50 ms恒流激励的情况下，发火件的发火是由于金属桥带爆发产生的高温高压的气体侵入药剂而引起药剂发火的，即这种情况下发火件的发火方式是电爆发火。

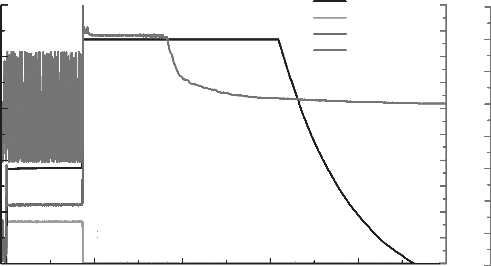
图4.13　2#样品/Zr/KClO4激励电流4 A发火，同时桥断

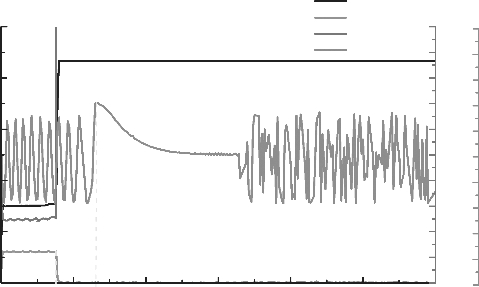
图4.14　2#样品/BNCP激励电流3 A先断桥，后发火

2. 实验与理论对比

由实验现象分析可知，50 ms恒流激励情况下，发火件的发火属于电爆发火方式，所以本书将金属桥带发火件50 ms恒流激励模式下的发火条件作如下定义：金属桥带的温度达到其爆发点（熔点）时，发火件发火。根据这个定义，按照式（4-6）～式（4-8）的差分表达式，利用MATLAB软件计算50 ms恒流激励时的临界发火电流，并将其与实验结果进行对比，如表4.15所示。

表4.15　50 ms恒流激励时桥带发火件临界发火电流的理论计算值与实验值对比

从表4.15可知，发火件的临界发火电流的计算值与实验值的误差都在15%以内，两者比较接近，所以可以用这种方法来估算50 ms恒流激励下金属桥带发火件的临界发火电流的值。