金属桥带发火组件的工作原理

1. 发火模型

由于发火件发火区相对于药剂和塞子而言非常小，所以可以将发火区看作一个热点，而将药剂和塞子看成两个半球体，其中药剂半球的半径取与塞子半径相等的值。为了使模型简化，需作如下假设：① 忽略电桥和药剂以及电桥和塞子接触面之间的接触热阻和热容，即交界面处三者的温度相等；② 忽略药剂的化学反应放热，即认为药剂为惰性物质；③ 电桥以均匀的热流密度向药剂和塞子传递热量，并且只存在热传导这一种传热方式，不考虑桥和药剂以及塞子之间辐射形式的散热；④ 假设桥带、药剂和塞子都是均匀且各向同性的物质，并且桥带和塞子的性质相同；⑤ 在整个过程中，桥、药剂和塞子的导热系数、密度、比热容等均不随时间变化。

2. 数理模型

根据上述假设，桥带-药剂-塞子系统的传热问题可以归结为一维球体非稳态导热问题，由于桥带-药剂半球和桥带-塞子半球是对称的，这样可以先选择桥带-药剂半球为研究对象，传热方程与定解条件可表述如下：

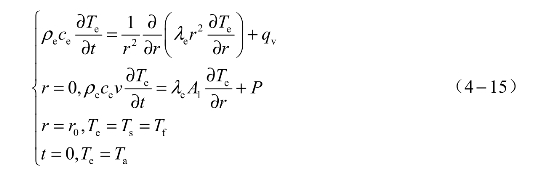
式中，Te为药剂温度（K）；Ts为塞子温度（K）；Tf为桥带温度（K）；ρe为桥带密度（kg/m3）；ce为桥带的比热容（J/（kg·K））；λe为桥带导热系数（W/（m·K））；r为半球系统半径（m）；A1为桥带总面积（m2）；qv为单位体积的内热源热量，在桥带区域（0≤r≤r0），内热源为桥带产生的焦耳热：

(www.xing528.com)

式中，v为桥带发火区的体积（m3）。

在药剂区域（r＞r0），内热源为药剂的化学反应放热，但是由于这部分热量非常小，可忽略不计，即

由对称性可得桥带-药剂系统的传热方程和定解条件如下：

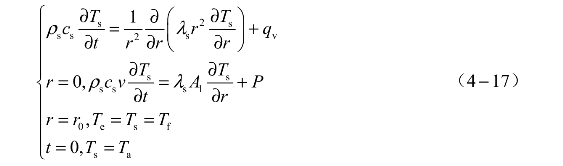
由式（4-15）～式（4-17）即可求出药剂-桥带-塞子系统的温度分布。由于方程比较复杂，没有解析解，可采用差分的方法进行求解。