金属电爆炸的模型探究

3.4.3.1 一维电爆炸模型

图3.33所示为桥箔起爆电路的电路图，由火花隙开关、电容和桥箔组成，是一个典型的电容放电回路，由基尔霍夫定理得到回路方程为

式中，R0和L分别表示整个放电回路的分布电阻和电感；Q0表示储能电容器上开始放电时的初始电荷；R是箔桥电阻，随温度变化为非线性关系。初始条件Q(0)=CU0，(dI/dt)0=U0/L，其中C、U0、L分别为系统电容、充电电压和回路电感。

金属箔电爆炸过程是在导体通过电流后，迅速被加热到熔点，转变为液体。由于惯性和磁力约束的作用，它仍保持一定的形状；此后，过热的液态金属更快地被加热达到沸点，热能使原子激发，破坏材料的化学键后，开始汽化，汽化波首先从导体的表面向中心运动，汽化的金属蒸气具有高压力，以致在外电场和晶格固有电场综合作用下使电子运动受阻。其电阻不断增加，当导体全部汽化时，导体电阻陡然增加，电流突然下降。在汽化开始后，金属蒸气同时不断向外部膨胀，其内压力降低和密度减小或形成等离子体时，蒸气导体恢复导电。只有当向导体输入的能量大于或等于导体汽化所需要的能量时，导体才会发生爆炸，否则导体会像普通保险丝那样熔化。导体电爆炸过程呈现一个明显的非线性电阻，它对电流脉冲有着重要的影响，即回路中的电流脉冲在很大程度上是由导体爆炸过程决定的。图3.34所示为俄罗斯研究人员通过实验获得的相对电阻与比输入能量的关系曲线，也说明了上述过程。

图3.33　桥箔发火电路图

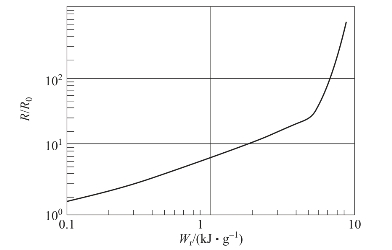
图3.34　铝箔相对电阻与比输入能量的实验关系曲线

从上面的分析可以看出，桥箔加热过程的动态电阻强烈地依赖于温度和导体的密度，所以得到整个金属爆炸扩展过程中电阻率的理想模型是非常复杂的。为了使计算简便，Ronald S.Lee对于大尺寸导体在大电容放电条件下的金属电爆炸进行数值模拟。编制了程序FIRESET[27]，利用它模拟的结果与实验结果具有较好的一致性。下面进行详细介绍。

从导体电爆炸的分类可知，通过导体的电流密度决定了导体爆炸的情况。电流密度对时间的积分定义为比作用量

由于j(t)比较容易测量，同时大量的实验也表明，到爆炸时刻tb比作用量g0的值近似是一个常数，与桥箔截面和电流波形没有具体关系，因此如果j(t)可以计算，那么就可以预估爆发时间和电流。不过电流密度必须达到金属电爆炸的强度，这个关系式才有意义。

由于实验R(g)有一峰值，同时爆炸后，电阻率比较大且基本为常数，为此Ronald S. Lee选用高斯函数作为电阻率表达式。

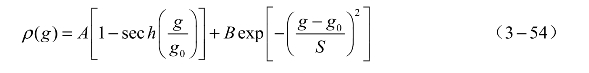
式中，A为爆炸后的电阻率；B为电阻率峰值；S为电阻率峰的宽度；g0为爆炸时刻的比作用量。这样就保证了电阻率爆炸前后的连续性，则

通过比作用与初始电流取对数作图，能够满足直线关系，所以，

通过实验数据可以确定K、P和G0。通过大量实验，得到K=2×1011A/S，P =0.19，计算结果表明，计算结果对P的选择不敏感。其他参数对铜A=100Ω·cm，B=200Ω·cm ，G0=2.5×109A2s/cm4，S0=2.5×108A2s/cm4。如果令

微分上式得

式中，Cs为导体横截面积。对上式积分可以求出电流和比作用量，以及桥箔上的电压和桥箔上的功率。利用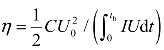可以求出加热桥箔的能量利用率，U是桥箔两端的电压。

3.4.3.2 二维金属箔电爆炸数学模型

上一节介绍的FIRESET模型比较简单，充分利用在爆炸参数一定范围内，爆发时刻的比作用量基本保持不变的特性，建立起了电阻率与比作用量的关系，通过实验数据修正关系式中的参数。虽然它的计算结果与实验数据具有比较好的一致性，为电爆炸桥箔的设计提供了一个简单的预估方法。但是实验也发现桥箔形状的改变会影响到爆发特性，影响多大？需要建立二维模型来考虑，即要考虑桥箔长和宽对爆发特性的影响。

1. 基本假设

（1） 趋肤效应可以忽略：由于桥箔厚度只有5 μm左右，而脉冲功率源短路放电周期为600 ns左右，由表3.16可知，趋肤深度远大于所研究的桥箔厚度，因此趋肤效应可以忽略。

（2） 桥箔厚度同桥箔长和宽相比要小得多，所以在不考虑趋肤效应的情况下，认为在厚度方向上温度是均匀的。

（3） 桥箔密度在爆发前为常数，此时密度的作用主要体现在计算箔桥质量及形成金属蒸气的压力上，爆发后密度变化。

（4） 热容CV与温度的关系熔化前由实验确定，熔化时由Grover液态金属状态方程计算得到，温度更高时，由考虑电子贡献的理想气体定律计算得到。

（5） 假设加热过程在等容条件下进行，由于本书研究的桥箔爆炸时间小于0.4 μs，熔化到爆炸的时间间隔小于0.2 μs，因此在这样一个相对短的时间范围内，定容的假设在物理上是合理的。

（6） 忽略热传导和热辐射。

2. 金属箔电爆炸过程的数学模型

在FIRESET模型中，没有考虑桥箔长宽的影响，电流为集总电流。而对于考虑长宽变化时，由于电流分布不均匀，导致桥箔温度不均匀，从而会出现桥箔某一点首先爆炸。因此必须考虑电位分布，以确定给定时刻的电流分布。根据实际情况，桥箔是由两端等腰梯形的“地”和中间方形的“桥”两部分组成，如图3.35所示。

图3.35　桥箔的形状

把桥箔在Y方向上的电位归一化，归一化电位由如下方程定义：

式中，E为导体中电场的强度；φ为归一化电位。归一化电位在桥箔区域上满足第二类椭圆型偏微分方程：

式中，σ为金属桥箔的电导率。式（3-59）在桥箔区域上可以改写为

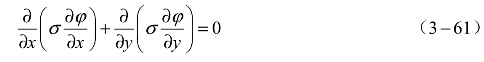
边界条件：

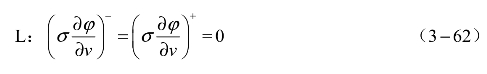
式中，v为边界Γ0的外法线方向。

通过求解归一化电位，可以进一步求解在归一化下的电流密度j→和回路电流I→。在归一

化下的电流密度为

在归一化下的回路电流为

非线性电阻元件的电阻为

回路电流由以下差分方程：

得到，由此求出第n + 1时刻的电流In+1。在初始时刻n = 0，I = 0，Q = Q0。

加在桥箔上的瞬时电压为

桥箔上的瞬时功率为

实际的电流密度为

桥箔的比作用量为

式中，A为导体的横截面积。

温度随时间的变化率为

式中，CV为定容热容；ρ为桥箔的密度；σ为电导率。求解上述方程组可以得到在桥箔不同位置温度分布和爆发点的位置。

3. 金属箔电爆炸过程电导率

在上一节模型中CV、ρ、σ是重要的物理参量，其中电导率在桥箔的加热过程中随着金属相态的变化也发生着剧烈变化。在数值模拟过程中，研究电导率随温度变化的关系就尤为重要。下面将对电阻率的变化进行详细分析。

1） 桥箔加热初始阶段电阻率随温度的变化

所有金属的电导率在一定的温度范围内都随温度的升高而降低。研究表明，几乎所有金属导体的电导率都与温度之间近似地有如下关系：

(www.xing528.com)

即电阻率与温度成非线性关系。其中0σ是在温度T0时的电导率，α 是电阻率随温度的变化率。常用的桥箔材料是Cu、Al、Au，它们的这三个常数值见表3.17。

表3.17　常用桥箔材料常数

例如，在此阶段铜的电导率为

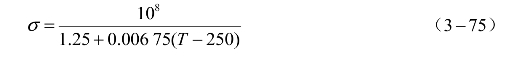
对铜和铝的电导率实验和计算表明，当温度T＜3 000 K时，其电导率与温度的关系可以与式（3-74）很好地近似。

2） 桥箔本征爆炸阶段

强电流脉冲加热铜箔或铝箔金属使温度从3 000 K上升到约8 000 K的过程中，对应金属从汽化的亚稳态向平衡两相态的剧烈转变，该相变伴随着由密度的热力学涨落增强而引起金属导电性急剧降低。这个过程中金属的电导率可按式（3-75）估计：

式中，en为电子浓度，由下式确定：

式中，v表示比容，在此阶段金属膨胀的影响比较明显，假定比容在汽化开始后随温度成线性膨胀，即

对铜来说，β的估算值为2.55 × 10-6，T1为3 000 K，v0为铜在常态下的比容0.11 cm3/g。T表示温度。是费米-狄拉克（Fermi-Dirac）函数，即

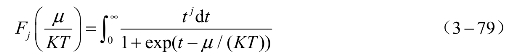
式中，μ为金属的化学势，铜的化学势为

式中，K为玻耳兹曼常量；μ0为铜在零温度时的化学势，即μ0=7.04eV 。

na 为原子浓度，由下式确定：

k为修正系数，对铜估算值为234.0 Ω-1·m-1；0a为波尔半径，即

式中，h表示普朗克常量；em表示电子质量；e表示基本电荷。

γv为金属体积膨胀系数，对于铜γv=6.8×10-4g/J；z为离子等效电荷。

利用上述各变量代入式（3-75）就能求出不同温度下桥箔的电导率。

3） 等离子体阶段

在强电流脉冲迅速加热情况下，桥箔迅速汽化而膨胀，当密度降到一定程度时，在强电场的作用下，部分气体开始电离，形成的有自由电子气简并部分电离的稠密等离子体，为此采用适合固态、凝聚态、稠密等离子的Lee-More模型[28]，其形式为

式中，ne为电子浓度。根据Saha电离平衡方程和自由电子态密度8πpdp2/h2，考虑费米-狄拉克分布后，最终确定此阶段电子浓度ne表达式为

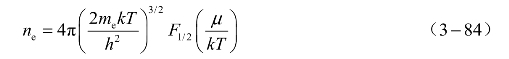
e为电子电量，τ为电子能量弛豫时间，对部分电离等离子体要考虑简并效应，于是

式中，ni为离子数密度；lnΛ是库仑对数。

bmax 和bmin分别为最大和最小碰撞参数，形式为

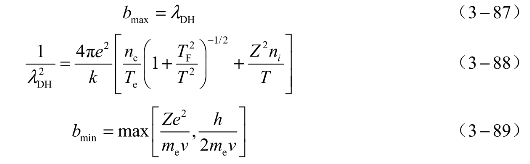
式中，TF是费米温度：

对于铜箔来说，bmin应取后者，即

系数αA可由费米-狄拉克积分来表示：

将上述关系式整理化简后得

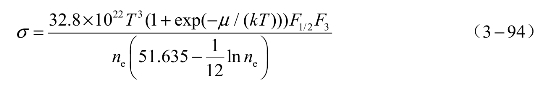
综上所述，铜的电导率与温度的关系可归纳为以下三个式子：

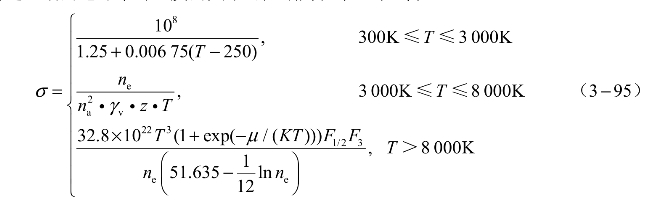
图3.36表示铜的电导率随温度的变化关系，随着温度的升高，电导率迅速下降，当下降到某一值时，电导率开始增加，其分别对应于固态加热、熔化和等离子态电导率随温度的变化关系。

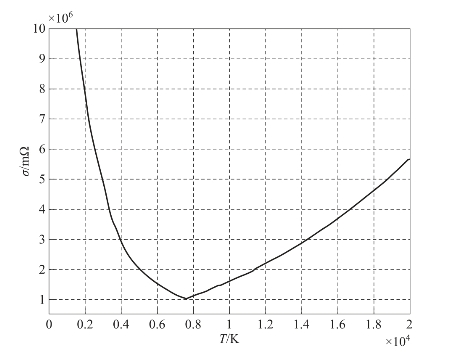
图3.36　电导率随温度的变化关系

3.4.3.3 金属电爆炸数值模拟实验结果的对比分析

1. 铜材料的实验与数值模拟结果分析

利用已建立的二维数学模型，对文献中有实验条件的实验进行了数值模拟，比较数值模拟结果和实验结果的差别，并与FIRESET计算结果进行了对比，以判断两个模型的模拟准确度和使用条件。FIRESET是目前模拟冲击片雷管预爆发阶段性能所普遍使用的一个软件，它的主要优点是数学模型简单易懂，模拟过程方便、快捷。本研究所采用的模型相对复杂，那么在保证模拟结果准确度的情况下，尽可能使用简单模型，以方便工程设计中的应用。

图3.37～图3.40和表3.18是一组实验参数与用本章模型和FIRESET模型计算得到数据的比较。电路参数：电压7.3 kV，电容0.25 μF，电感215 nH，线路电阻0.323 Ω。桥箔尺寸：A为0.4 mm × 0.4 mm × 5 μm；B为0.8 mm × 0.8 mm × 5 μm；C为1.0 mm × 1.0 mm × 5 μm；D为1.17 mm × 1.17 mm × 5 μm。

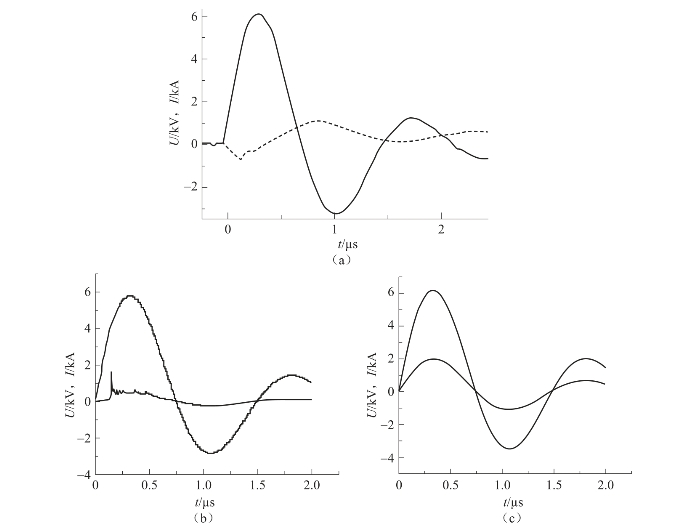
图3.37　桥箔A爆发电流和电压

（a）桥箔A的电流-电压曲线实验值；（b）本书模型计算结果；（c）FIRESET计算结果

从图3.37～图3.40可以看出，二维模型与实验曲线在爆炸点附近电压曲线都有一个尖峰，二维模型更能够反映爆炸箔的爆发特性；而FIRESET计算得到的电压曲线比较平滑，没有尖峰的出现，不能够很好地反映出爆发点的位置。

表3.18和表3.19是A、B、C、D四个尺寸的桥箔实验与两个模型计算数据的比较。Ib1为爆炸时电流实验值，Ib2为爆炸时电流计算值，Vb1为爆炸时电压实验值，Vb2为爆炸时电压计算值，tb1为爆发时刻实验值，tb2为爆发时刻计算值，I1为峰值电流实验值，I2为峰值电流计算值，t1代表峰值时刻实验值，t2为峰值时刻计算值。

图3.38　桥箔B爆发电流和电压

（a）爆发电流-电压曲线实验值；（b）桥箔B本书计算结果；（c）桥箔B FIRESET计算结果

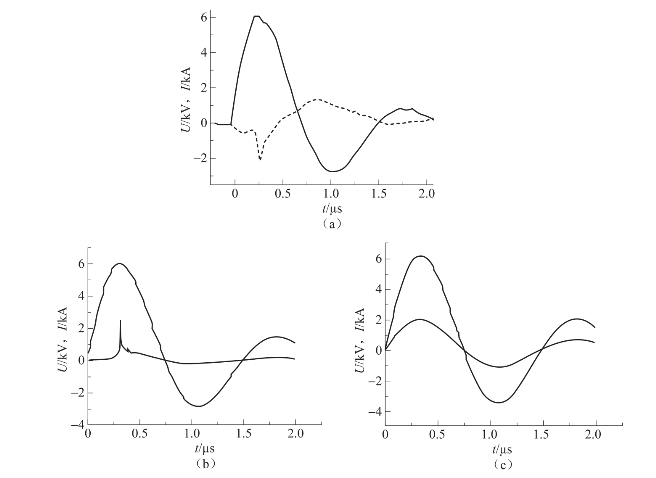
图3.39　桥箔C爆发电流和电压

（a）桥箔C的电流-电压曲线实验值；（b）桥箔C本书计算结果；（c）桥箔C FIRESET计算结果

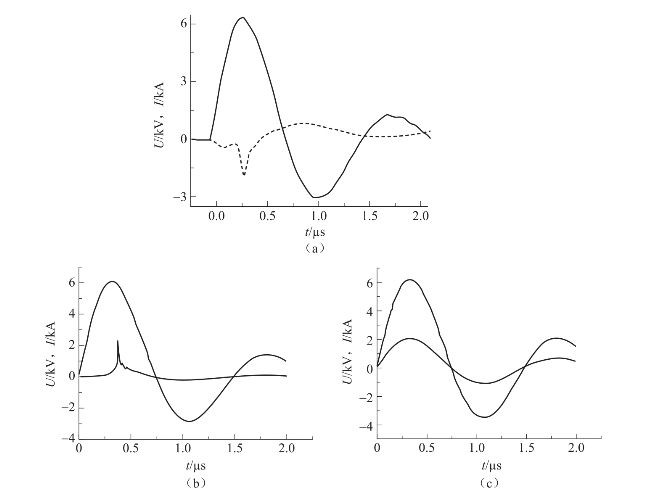
图3.40　桥箔D爆发电流和电压

（a）桥箔D的电流-电压曲线实验值；（b）桥箔D本书计算结果；（c）桥箔D FIRESET计算结果

表3.18　不同尺寸桥箔条件下模拟计算与实验值的比较

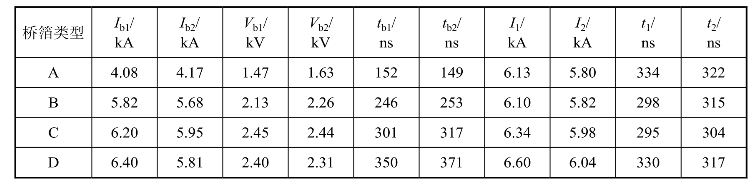
表3.19　不同尺寸桥箔条件下FIRESET模型与实验值的比较

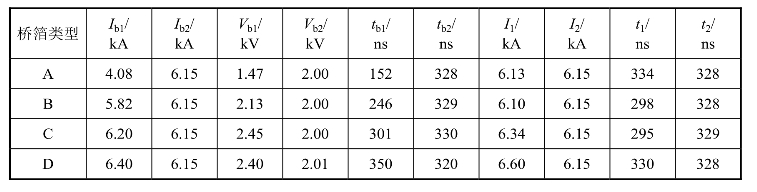
表3.20　两种模型的误差分析

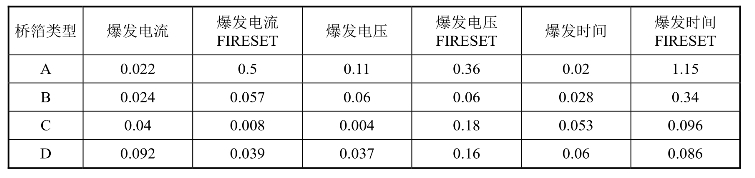
从表3.19和表3.20中的数据可以看出，在厚度及电路参数不变的情况下，由于FIRESET假定比作用量不随桥箔尺寸变化，而比作用量又是电阻率、电流密度的函数，因此导致当正方形的桥箔从0.4 mm到1.17 mm变化时，爆发电流、时间、电压变化不大，整个计算的误差也比较大，不能很好地反映实际情况。