SCB电火工品的恒流激励和电容放电激励下的换能模型及数学方程

SCB电火工品的能量加载方式主要有恒流激励和电容放电激励两种，下面分别介绍在这两种情况下SCB换能元的换能模型。

3.3.3.1 恒流激励

1. 基本假设

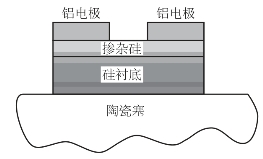
SCB结构如图3.24所示，在恒流激励下，SCB换能元属于电热换能，即将电能转化为焦耳热使自身温度升高外，同时将热量传递给金属电极、衬底和陶瓷塞。当输入电流低于某一临界值时，SCB温度经历了先上升然后趋于稳定的过程，最终保持热平衡态。SCB热平衡态是指得热和散热相等的一种平衡状态，平衡态的临界性分析目的是获得SCB的临界爆发电流。为了得到解析解，必须使模型简化，需作如下假设：

（1） 将SCB看作半径为r0温度分布均匀的热点，选取以SCB为中心的半球形塞子为研究对象，将塞子的半径作为半球的外径，如图3.25所示。只考虑塞子半球表面的散热，忽略桥向空气的直接散热。

（2） SCB与塞子的物化性质相同，SCB衬底与塞子紧密接触，忽略交界面间的接触热阻和热容。

（3） 桥以均匀的热流密度只沿塞子的径向传递热量，只考虑热传导这一种传热方式。

（4） 在整个响应过程中，塞子的导热系数、密度、比热容等均不随温度变化。

(www.xing528.com)

图3.24　SCB结构

图3.25　恒流激励下SCB换能元物理模型

2. 数学方程

当SCB进入热平衡态后系统温度不再随时间改变，满足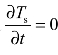。基于以上假设，塞子的导热可归结为一维球体稳态导热问题，且具有第三类边界条件[24,25]。根据能量守恒原理，以热点（SCB）中心为坐标原点建立球坐标系，桥塞系统的导热微分方程和定解条件可描述为

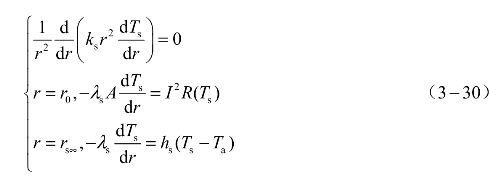
式中，ks为塞子的热扩散率，ks=λs/(ρscs )；ρs为塞子密度（kg/m3）；λs为塞子导热系数（W/（m·K））；cs为塞子的比热容（J/（kg·K））；hs为塞子的表面传热系数（W/（m2·K））；rs∞为塞子的等效半径（m）；A为SCB面积（m2），。SCB电阻R与温度T之间的关系见式（3-29）。

式（3-30）中第一个表达式为系统的温度控制方程，不含内热源；第二个表达式为衬底与SCB桥膜接触的边界，表示传入半球的热量等于桥膜产生的焦耳热；第三个表达式为塞子与空气接触的边界，表示传出半球的热量等于塞子散失到空气中的热量，满足牛顿冷却定律。