直线的标高投影及计算方法

直线上任意两点的标高投影即为该直线的标高投影。

1.直线的坡度与平距

直线的坡度就是直线上任意两点的高差与其水平投影的比值，用i表示。如图8-3所示，直线上A、B两点的高差为ΔH，水平投影的长度为L，直线AB对H面的倾角为α，则得:

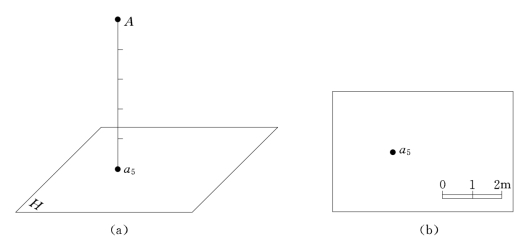
图8-2　点的标高投影

（a）空间分析；（b）标高投影图

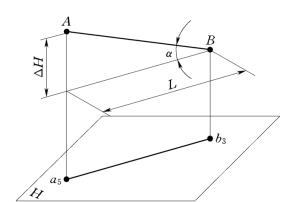
图8-3　直线的坡度

直线的平距是指直线上两点的高差为1时的水平投影的距离，用l表示。平距与坡度互为倒数。

2.直线的标高投影表示法

直线的标高投影常用以下几种形式表示:

（1）用直线上任意两点的标高投影来表示，如图8-4（a）所示。

（2）用直线上一点的标高投影和直线的坡度（箭头指向下坡方向）来表示，如图8-4（b）所示。(www.xing528.com)

（3）水平线的标高投影可用该直线的水平投影并加注高程来表示，如图8-4（c）所示。

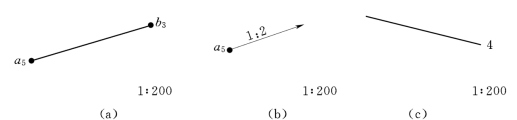
图8-4　直线的标高投影表示法

（a）两点表示法；（b）一点和坡度表示法；（c）水平线表示法

【例8-1】 如图8-5（a）所示，已知直线AB的标高投影a 3.5b 8.5和k点位置，求直线上高程为4m、5m、6m、7m、8m的整数高程点的标高投影和直线上k点的高程。

分析:已知直线的坡度，可以根据坡度求出直线上任意高程点的标高投影；反之，已知直线上某高程点的位置，也能计算出该点的高程。

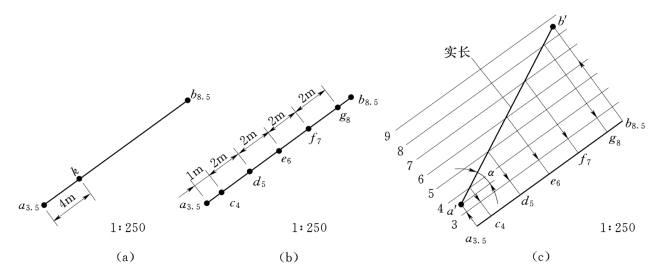
图8-5　直线上高程点的求法

（a）已知；（b）计算法求整数高程点；（c）图解法求整数高程点

因直线的标高投影已知，所以可求出该直线的坡度i与平距l。直线段上各整数高程点的标高投影可用计算法或图解法求得。已知L ak=4m，根据ΔH=Li即可求得ΔH ak，进而可求出k点的高程。

作图:

（1）求整数高程点。

1）计算法。由已知条件可知:ΔH ab=H b-H a=8.5-3.5=5m，再用图中比例尺量得L ab=10m，即可计算得出直线坡度i=ΔH ab/L ab=5/10=1/2、直线平距l=1/i=2m。因L=ΔHl，高程为4的点距A点的水平投影距离L 1=（4-3.5）×2=0.5×2=1m，高程为4m、5m、6m、7m、8m的点之间的水平距离均为2m，根据比例依次量取，即得各点标高投影，如图8-5（b）所示。

2）图解法。作辅助铅垂投影面V∥AB，在V面上按适当比例作相应整数高程的水平线（水平线∥ab，最低一条高程为3m，最高一条高程为9m，包括直线两端点高程即可），再根据A、B两点的高程在V面上画出直线AB的V面投影a′b′，从a′b′与各整数标高的水平线的交点，向ab作垂线，垂足8、7、6、5、4即为直线上的整数高程点。作辅助正面投影时所采用的比例与标高投影的比例一致，则a′b′反映实长，它与水平线的夹角反映直线AB对H面的倾角，如图8-5（c）所示。

（2）求k点的高程。已知，L ak=4m，i=1/2，则A、C两点高差ΔH ak=H k-H a=L ak i=4×1/2=2m。由此可得，H k=ΔH ak+H a=2+3.5=5.5m，即k点的高程为5.5m。