实时仿真电磁-机电暂态混合基本原理

10.3.1.1 电力系统电磁暂态过程的计算方法

电磁暂态过程是指在电力系统各元件的作用下，相应的电场、磁场、电压、电流的变化过程。由于电磁暂态过程一般都变化很快，需要分析和计算时间间隔在毫秒级以内的电参量瞬时值变化情况，而且还需要考虑元件的非线性、输电线路分布参数所引起的波过程，以及线路三相结构不对称、线路参数的频率特性以及电晕等因素的影响。因此，在电磁暂态仿真中一般采用abc三相瞬时值进行计算，输电线等网络元件采用含电容、电感、电阻的微分方程或偏微分方程描述，发电机采用dq0电压方程或abc三相电压方程、磁链方程和运动方程的形式描述，对FACTS和HVDC系统采用电力电子开关器件模型描述，并考虑其缓冲电路的影响。

目前得到广泛应用的电磁暂态分析方法主要有Z变换分析法、状态变量法、离散网络法和暂态网络分析（TNA）等。其中离散网络法是将电力系统中的并联电抗器、并联和串联电容器等集中参数元件，或可以近似处理成集中参数的元件（如变压器和短线路）的电压和电流间关系用常微分方程（纯电阻参数元件则为代数方程）描述，然后应用数值方法进行求解。由于隐式梯形积分法比较简单而且具有相当的精度和良好的数值稳定性，并能较好地适应刚性微分方程组，因此在电磁暂态程序中常采用这种积分方法。

在一个积分步长内，通过数值积分的计算方法将常微分方程转换为相应的差分方程，该方程描述了系统t时刻的电压、电流与t-Δt时刻的电压、电流之间的关系。差分方程描述的系统电磁暂态求解关系式可以用一种由纯电阻和电流源构成的电路来代替，以反映t时刻未知电压、电流和t-Δt时刻的电压、电流值之间的关系，其中电阻的大小取决于元件的参数和积分步长，而电流源的大小由t-Δt时刻的电压和电流值决定。因此网络的求解可以表示为如式（10-1）所示的代数方程组的形式。

G·V（t）=I（t-Δt） （10-1）

式中，G表示电网络等效导纳矩阵，为常系数矩阵，在系统网络参数或拓扑结构发生变化时才改变；V（t）为电网络各个节点电压的列向量；I（t-Δt）为t-Δt时刻网络的等效电流源列向量。

通过求解一系列离散时间点的系统状态量，进而求出系统在预设的整个时间段内的状态量变化曲线，从而完成系统的电磁暂态仿真计算^[19]。本书介绍的混合仿真中的电磁暂态仿真是采用实时数字仿真器（RTDS）实现的，而后面的机电暂态仿真以及接口模型则是基于该仿真系统采用自定义编程实现的。

10.3.1.2 电力系统机电暂态过程计算方法

机电暂态仿真计算是基于系统运行于工频正弦波状态的假设，系统变量采用基波相量来表示，将三相电气网络经过线性变换转化为相互解耦的正、负、零序网络分别求解，发电机可以采用降阶的实用模型，FACTS装置和HVDC系统采用工频准稳态模型，忽略其换流器本身的暂态过程。

机电暂态仿真计算的数学模型主要包括两大部分：发电机微分方程组和电力网络的代数方程组。发电机的微分方程组可以包括：①转子运动方程；②发电机暂态和次暂态电动势变化的微分方程；③励磁系统调节系统动态特性的微分方程；④调速器调节系统动态行为的微分方程。

电力网络部分包括各电压等级的输电线路和变压器，采用等效的集中参数模型，忽略电磁暂态过程，电力网络采用如式（10-2）所示的节点电压方程组进行求解。

I=YU （10-2）

式中，I为网络各个节点的注入电流列向量；Y为系统的节点导纳矩阵，当系统拓扑结构不变时，该矩阵为不变的复矩阵；U为网络各个节点的电压列向量。

机电暂态仿真计算的系统方程可以表示为发电机微分方程组和电力网络的代数方程组的联立方程组，如式（10-3）所示。

式中，x表示状态变量列向量；y表示系统的代数变量列向量；f、g为对应维数的函数阵。

目前，对式（10-3）所示的微分代数方程组的求解主要有两种计算方法：交替求解法和联立求解法。其中交替求解法是当前机电暂态计算程序采用的主要方法，该方法采用隐式梯形积分法迭代求解系统所有发电机的微分方程组；采用直接三角分解和迭代相结合的方法求解网络的代数方程组。(www.xing528.com)

本书中所采用的是在RTDS上开发的电磁-机电暂态混合实时仿真平台。RTDS能够实现电力系统电磁暂态仿真的实时计算，但是还需要开发能实时计算的机电暂态仿真程序。为此开发了基于RTDS/CBuilder的实时机电暂态仿真计算程序，该模块在一块高速处理器板卡（GPC）上运行，在一定的规模限制下能够达到实时计算的要求，并且其计算精度已经经过了BPA等权威机电暂态计算软件的验证。

10.3.1.3 电磁-机电暂态的并行计算及接口方法

电磁-机电暂态混合实时仿真的原理结构如图10-7所示，电磁、机电部分通过专门开发的接口模块进行两侧的数据交换。

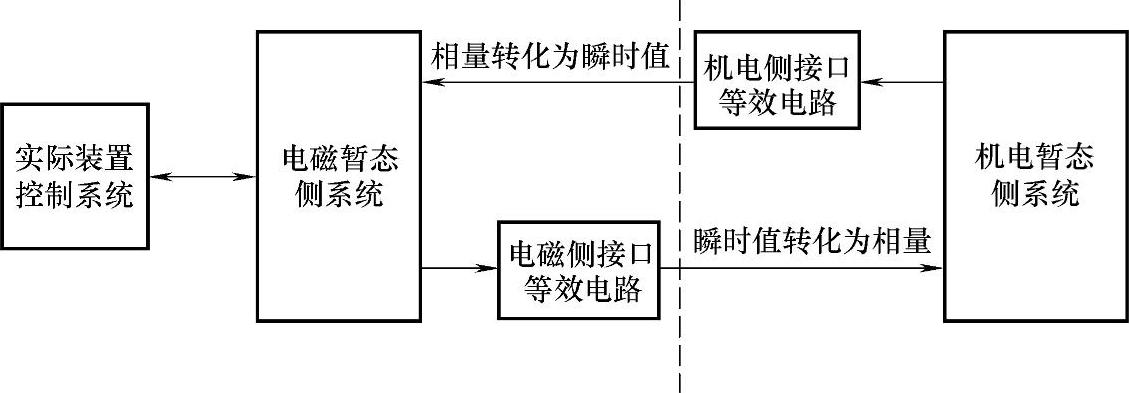
图10-7 混合实时仿真结构原理图

根据混合仿真计算的需要，按照待研究系统的结构特征，选择混合实时仿真的接口母线，在接口处将整个系统分成两个部分，对需要进行电磁暂态详细计算的部分作为电磁暂态侧系统，建立电磁暂态模型，而不需要详细研究的部分（通常为常规交流系统）作为机电暂态侧系统，则建立机电暂态模型。两部分分别通过各自的仿真计算程序并行计算，在一侧计算时，另一侧系统用其等效电路代替，当机电暂态程序完成一个时步的仿真计算时，两侧同时交换数据以更新其在对侧系统中的等效电路参数^[20]。

对于电磁暂态侧系统，与之相连的机电暂态侧实际上为一个有源系统，因此可以用一个戴维南电路作为其在电磁侧的接口等效电路，如图10-8所示。该接口模型需要与电磁暂态侧一起进行系统的电磁暂态过程求解，因此接口模块需要将机电暂态侧的相量值转换为电磁侧的abc三相瞬时值的形式。

对于机电暂态侧，与之相连的电磁暂态侧可以等效为一个PQ节点，由于机电暂态侧只进行系统工频相量的计算，因此需要利用电磁暂态侧系统接口母线电压、电流的瞬时值计算得到电磁侧向机电侧注入的工频有功、无功功率的值，计算模块数据转换结构如图10-9所示。

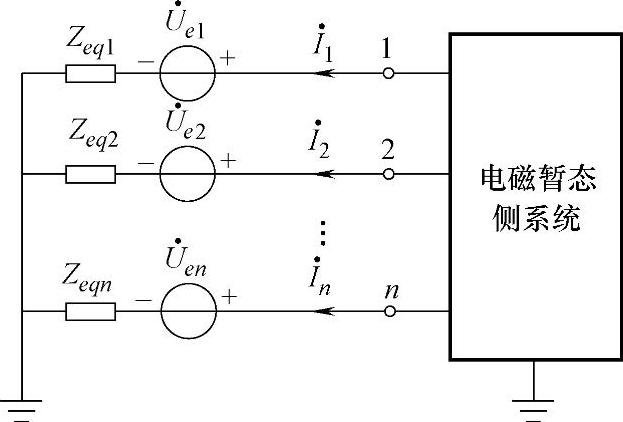
图10-8 机电侧的戴维南等效电路

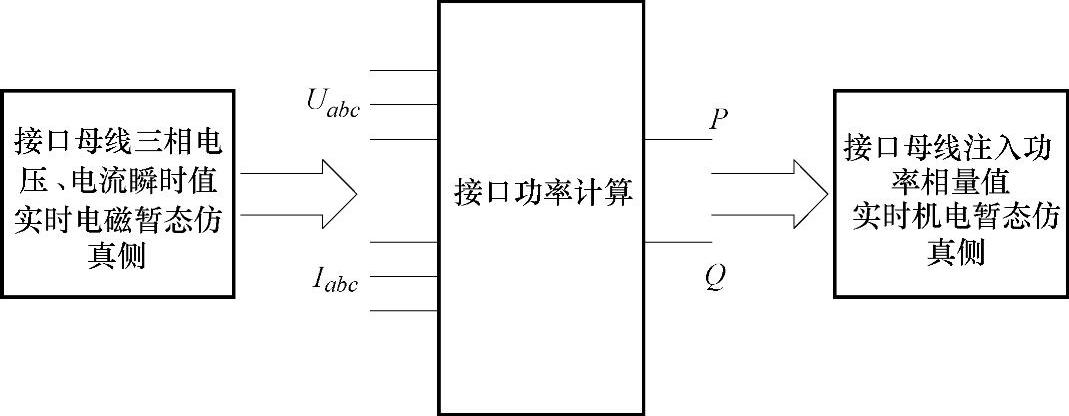
图10-9 接口处电磁侧功率计算模块

混合实时仿真的机电暂态侧和电磁暂态侧在数据交换的时间段内各自并行计算，因此两侧在仿真时不需要等待，在数据交换时刻采用并行数据交换时序，从而能够满足系统实时仿真的要求。在机电暂态侧完成一个时步的计算时，两侧系统就接口等效电路所需要的参数进行交换以更新参数，由于电磁暂态侧的功率计算需要交换时刻之前一段时间的数据，因此，该侧的计算相当于有一个延迟环节。混合实时仿真的并行数据交换方式如图10-10所示。

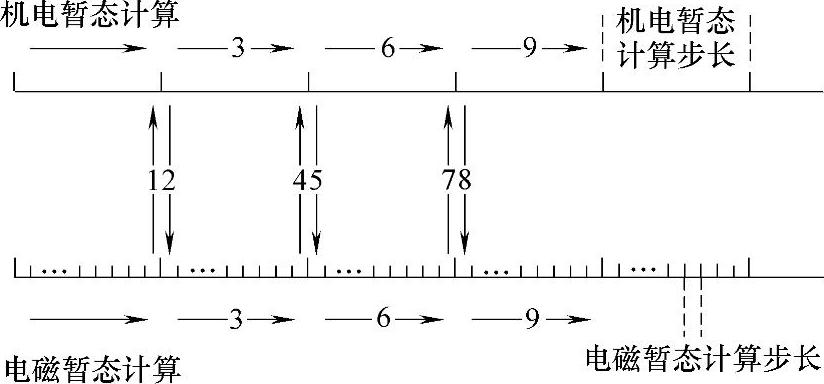
图10-10 混合实时仿真的并行交换时序

本书所采用的基于RTDS的电磁-机电暂态混合实时仿真技术，已经有多篇论文发表并介绍了研究成果^[21-27]，该混合实时仿真平台的正确性已得到了验证。下面介绍利用该混合实时仿真技术对电力系统次同步振荡的实时仿真进行探索性的研究。