直线上点的投影特性

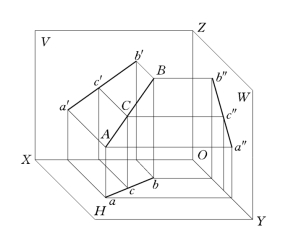
图2-21　直线上点的投影特性

如图2-21所示，AB直线上一点C，由图很容易得出，C点的投影一定在AB直线的同面投影上；C点将AB直线分为两段，两段长度比等于投影长度比。由此可得出直线上点的投影特性:点在直线上，点的投影在直线的同面投影上，并符合点的投影规律；直线上一点把直线分成两段，两段长度之比等于投影长度之比（定比定理）。

【例2-3】 判断点M是否在CD直线上。

(www.xing528.com)

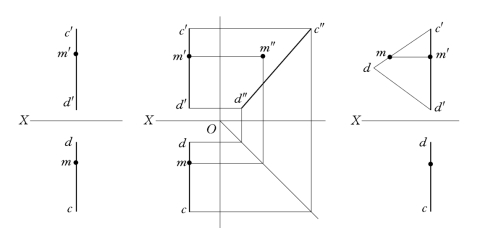
图2-22　直线上点的投影分析

分析:首先分析一下CD是什么直线。因为CD的正面投影和侧面投影都垂直于ox轴，说明CD直线上所有点的x坐标都相等，即直线上所有点到侧立面即W面的距离都相等，所以CD为侧平线。虽然M点的正面投影和侧面投影都在CD的同面投影上，但M点不一定在CD直线上。那么如何判断呢？有两种方法。一是分别作出CD直线和M点的侧面投影，若M点的侧面投影在CD直线的侧面投影上，说明M点在CD直线上，否则M点不在CD直线上。还有一种方法就是可根据比例来判断，若M点在CD直线上，应该有c′m′/d′m′=cm/dm。而这个等式是否存在，可通过几何作图判定。如图2-22所示。

下面具体作图。

解法一:先画出CD直线的侧面投影和M点的侧面投影，由点和直线的侧面投影可以看出，m″不在c″d″上，因此可判定M点不在直线CD上。

解法二:利用定比性作图，M点若在CD上，应有c′m′/d′m′=cm/dm，过c′作辅助线，在其上截取c′d′=cd，再截取c′m′=cm，由图可看出，c′m′/d′m′≠cm/dm，由此可判定M点不在直线CD上。