投影：正投影和斜投影的概念和应用

（一）投影的形成

如图2-1（a）所示，三角板在灯光的照射下在桌面上产生影子，可以看出，影子与物体本身的形状有一定的几何关系，人们将这种自然现象加以科学的抽象得出投影法。如图2-1（b）所示，将光源抽象为一点S，称为投影中心，投影中心与物体上各点（A、B、C）的投影连线（SAa、SBb、SCc）称为投射线，接受投影的面，称为投影面。过物体上各点（A、B、C）的投射线与投影面的交点称为这些点的投影。

（二）投影的分类

投影分为中心投影和平行投影两大类。

如图2-1所示，所有投射线都交于投影中心点S，这样的投影称为中心投影。

当把投影中心移到无穷远处时，所有的投影线都互相平行，这样的投影称为平行投影，如图2-2所示。

根据投影线与投影面是否垂直，平行投影又分为斜投影和正投影两种。当投影线倾斜于投影面时，称斜投影；投影线垂直于投影面时，称正投影。

工程图样一般都是采用正投影法绘制的，正投影法是本课程的研究重点。今后若不特殊说明，都是指正投影。(www.xing528.com)

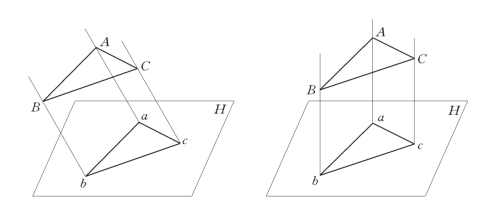
图2-2　平行投影法

（三）正投影的作法

空间点A，与投影面H，要作出空间点A在H面上的正投影，就要过空间点A作H面的垂线，垂线与H面的交点就是空间点A在H面上的投影。要作直线在H面上的投影，只要分别作出直线两端点在H面上的投影，连线即可。同理可作出平面图形的投影，如图2-

3所示。

图2-3　点、线、面的正投影的作法