测试系统仿真验证——高效优化实践

本节用如图7-1所示的测试系统通过时域仿真和信号的频谱分析来验证上述推导的结论。测试系统为单机-直流系统，汽轮发电机组转子为4质量块弹性轴系，测试系统的发电机组轴系参数如表7-1所示。

表7-1 测试系统发电机轴系参数

该交直流电力系统的次同步振荡将存在3个振荡模态，采用特征值分析法计算其自然扭振频率如表7-2所示。

表7-2 测试系统次同步振荡模态计算频率

当测试系统运行稳定后，在第10s发生瞬时三相接地故障，故障持续时间为0.1s，对汽轮机低压缸与发电机质量块间的扭矩（Te_LP-GEN）、转速（ω）、发电机端电压（u_t）、直流电压（u_dc）、直流功率（P_dc）进行频谱分析。

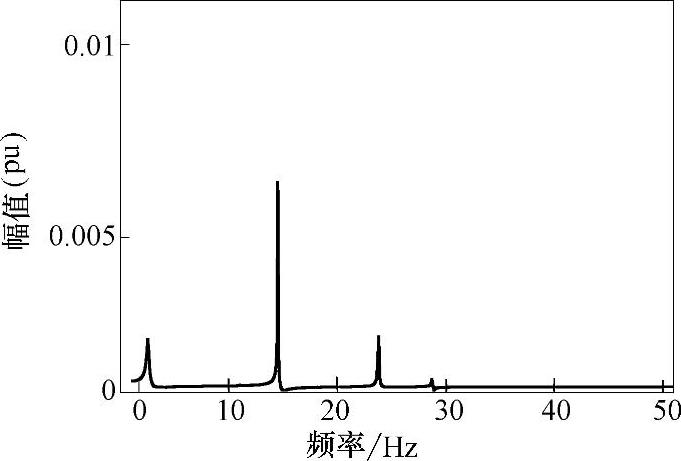
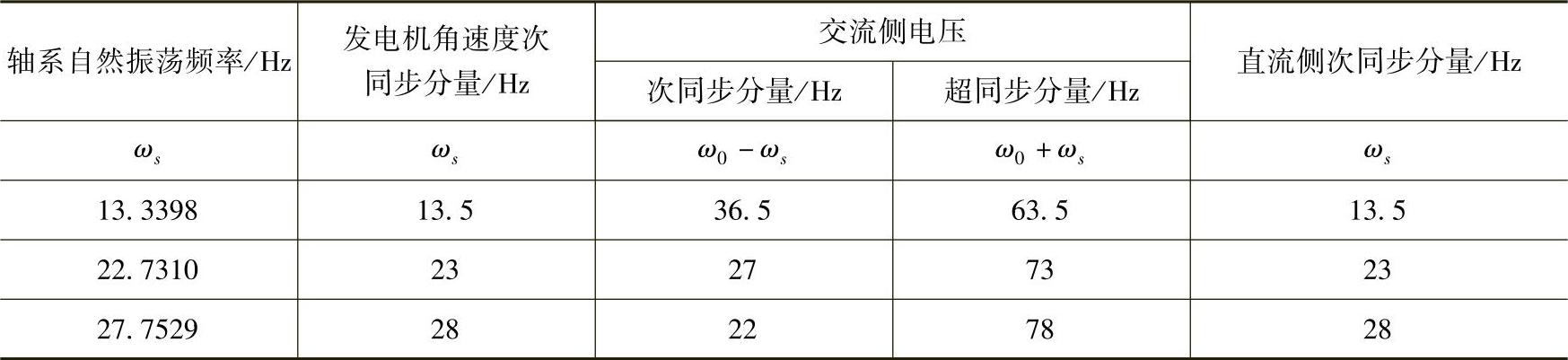
如图7-3和图7-4所示，当系统故障后引起次同步振荡时，汽轮发电机组轴系的扭矩和转速中存在轴系的三个自然扭振频率分量。图7-3中汽轮机低压缸与发电机质量块间的扭矩中有显著的13.5Hz、23Hz、28Hz的分量，与计算的轴系自然扭振频率基本一致。交流电网络中的电压中存在着与轴系自然扭振频率互补的次同步和超同步分量，从图7-5中可以看到，较显著的次同步频率为36.5Hz的分量，超同步分量的频率为63.5Hz。当然也存在次同步频率为22Hz、27Hz和超同步频率为73Hz、78Hz的分量，但由于这些次同步或超同步电压分量与工频量相比较仍然很小，因此在图中未能明显体现，表7-3给出了其中包含的所有次同步和超同步频率分量及其传递结果。

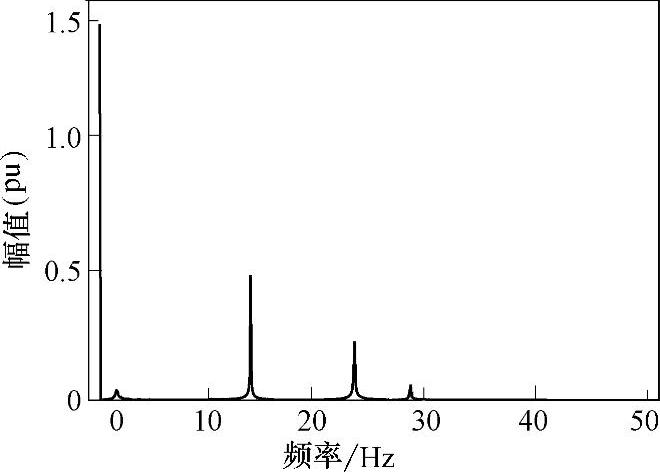
图7-3 Te_LP-GEN频谱图

(www.xing528.com)

图7-4 发电机转速ω频谱图

表7-3 系统次同步状态量的传递关系

如图7-6所示，直流功率中最显著的次同步分量频率分别为13.5Hz、23Hz、28Hz，与汽轮发电机组轴系的自然扭振频率基本对应。与交流网络电压中存在的次同步分量相似，直流功率中的次同步分量与直流量相比较也很小，幅值最大的次同步分量有效值约为直流量的0.083%。因此在研究由高压直流输电系统引起的电力系统次同步振荡时，无论是交流电网络中母线电压还是直流系统的直流功率中含有的次同步分量信号都十分微弱，与发电机组转矩和转速中的次同步分量相比，从中提取出需要阻尼的次同步频率分量很困难，这也给后续的SSDC的设计带来了一定的难度。

图7-5 发电机端电压u_t频谱图

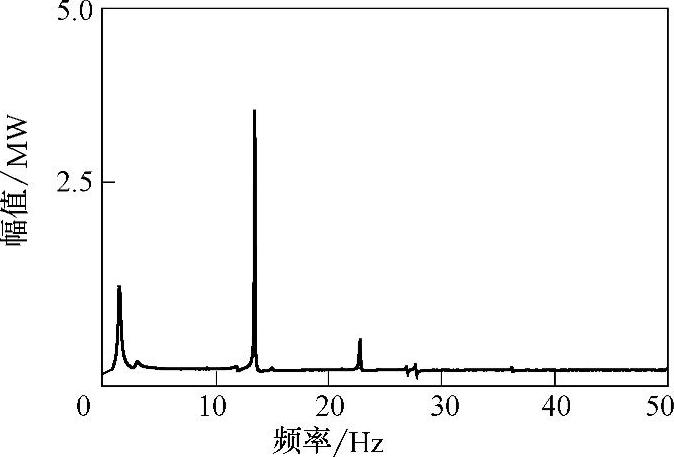
图7-6 直流功率P_dc频谱图

表7-3所示的在测试系统上进行的次同步振荡分量交直流侧相互传递和变换的仿真试验验证了7.2.3节推导的次同步频率变换关系。如果该次同步电压、电流形成的电磁功率与发电机转速偏差的相位差超过90°，在发电机的电磁力矩上将形成负的阻尼转矩，助增轴系扭振，最终导致发电机组失稳的次同步振荡^[7]。