次同步电流阻尼控制方法优化

6.4.2.1 系统接线

众所周知，实际中所使用的STATCOM主要用于提供无功功率、支撑系统电压以及提高输电系统的功率输送能力，与具有相同功能的SVC类似，一般也选择装设在线路的中间位置，以发挥其最大的功能。而采用该种接线方式时，仅通过常规的电压控制方式不能提供合适的正阻尼来消除次同步振荡，因此需在其控制器中附加阻尼控制环节^[17]。阻尼控制环节的输入信号取自线路电流的次同步分量，或通过WAMS（广域监测系统）技术测取发电机组的加速功率信号；与SVC相比，由于相同容量下，STATCOM占地面积更小，因此用于抑制发电机组次同步振荡的STATCOM可以借助厂用变压器并联接到发电机的出口母线上，或接于发电机升压变压器的高压侧，以便于获取包含发电机全部扭振模态的转速偏差信号，从而达到较好的抑制效果。下面以机端接线方式为例，对STATCOM抑制由串联补偿引发的次同步谐振的原理进行分析。系统接线如图6-28所示。

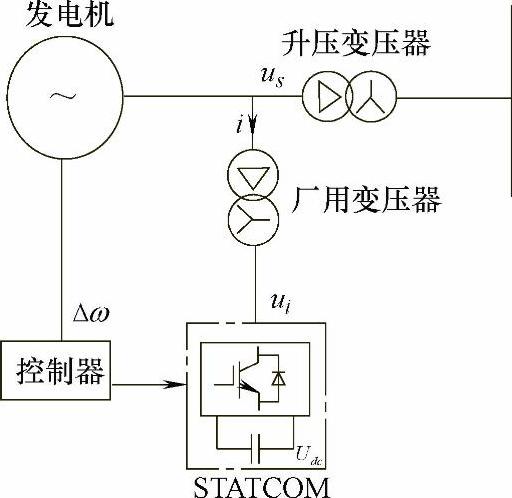
图6-28 用于SSO抑制的STATCOM系统连接图

6.4.2.2 原理分析

与用于抑制次同步振荡的SVC的原理相似，STATCOM也是以含有发电机组轴系扭振模态频率的检测量作为其控制器的输入信号，通过适当的控制算法，改变STATCOM注入系统的次同步电流大小，进而在发电机组的转子上产生阻尼次同步振荡的电磁转矩。与SVC不同之处在于，STATCOM是通过控制叠加在输出基波电压上的次同步分量来改变其注入系统的次同步电流的。

在利用STATCOM抑制次同步振荡的过程中，为了减小其注入系统的谐波，特别是为避免对发电机产生不好的影响，通常采用SPWM（正弦脉宽调制）对STATCOM中换流器的开关进行控制，这种控制方式将谐波频率限制在较高的开关频率附近，使得谐波对系统的影响大为降低。

以单相为例，假设SPWM的控制信号（也称调制信号）为

u_c=U_csin（ω₀t+θ_c） （6-29）

式中，ω₀=2πf₀为系统的基波角频率；f₀为系统的基波频率；U_c为控制信号的峰值；θ_c为控制信号的初相角。采用三角波作为载波信号，频率为f_s，峰值为U_tri。利用控制信号对载波信号进行调制，产生所需要的开关动作信号。其中开关动作的频率由载波信号，即三角波信号的频率f_s决定；STATCOM输出电压的基波频率等于调制信号的频率f₀，并且与调制信号波形同相位；STATCOM输出电压的峰值由直流侧的电容电压U_dc及控制信号与载波信号峰值的比值共同决定，由此STATCOM输出电压的基波可以表示为

u_i=m_aU_dcsin（ω₀t+θ_c） （6-30）

式中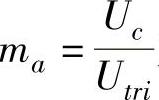，为幅值调制率。通常保持U_tri为常量，通过改变控制信号的幅值来改变装置输出电压的大小。

如果在三相控制信号中加入与发电机组轴系扭振频率相关的次同步和超同步分量时，控制信号可以表示为

式中，m_sub、m_sup分别为次同步和超同步频率电压分量的幅值；ω_m为发电机组轴系某一扭振频率；γ_sub、γ_sup分别为次同步和超同步频率电压分量的相位。利用该控制信号对三角波载波信号进行调制后，STATCOM的输出电压中除含有工频分量外，还存在次同步和超同步频率的电压分量。忽略了谐波分量后的输出电压为

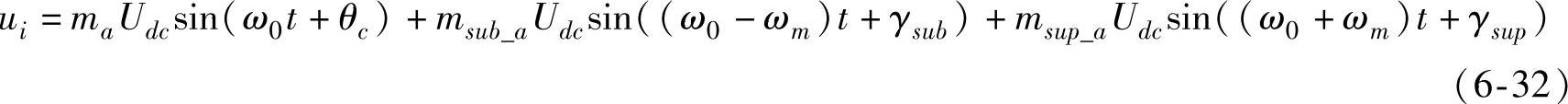
式中，为与次同步及超同步频率电压分量相对应的幅值调制率。

设系统电压为u_s=U_scos（ω₀t+θ_s），忽略耦合变压器的电阻，可以得到系统流入STAT-COM的电流为

式中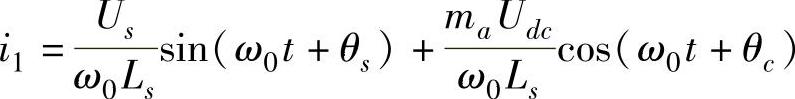，是由STATCOM产生的基频电流分量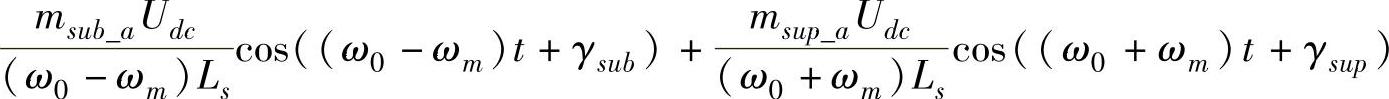；为STATCOM产生的次同步及超同步电流分量。

1.未接入STATCOM时系统的电气阻尼系数

IEEE第一标准模型在次同步频率下的线性化等效电路如图6-29所示。其中，ΔE_α为发电机感应次同步电动势，R与L′分别为发电机出口变压器及线路的电阻与电感，C为线路串联电容值，r_g与L_g为发电机等效电阻及电感。

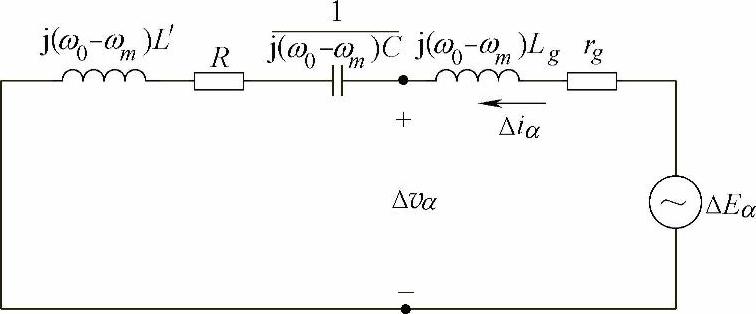
图6-29 未接入STATCOM的串补输电系统等效电路图

为便于分析，以下将在αβ静止坐标系下说明其原理，各变量及角度关系如图6-30所示。

图6-30 静止正交坐标αβ与dq坐标关系

由前述推导可知，发电机组的轴系按照其某一自然扭振频率振荡时，设其功角偏差为Δθ=Asin（ω_mt），发电机转速偏差为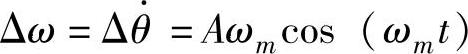。发电机在αβ坐标系下感应出的次同步电动势分量可以表示为

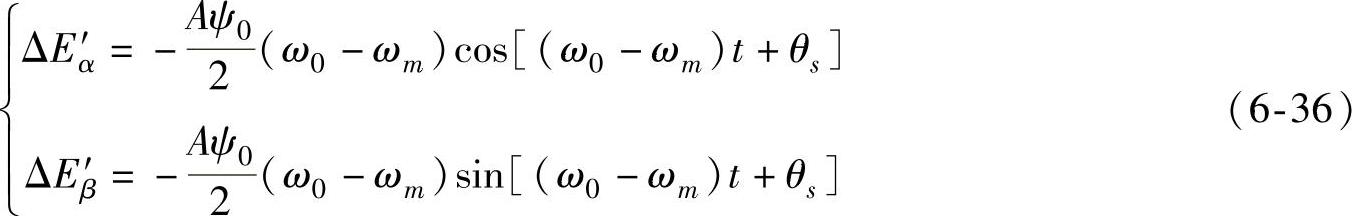
若在次同步频率ω₀-ω_m下线路发生谐振，即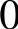，则αβ坐标系下次同步电流可表示为

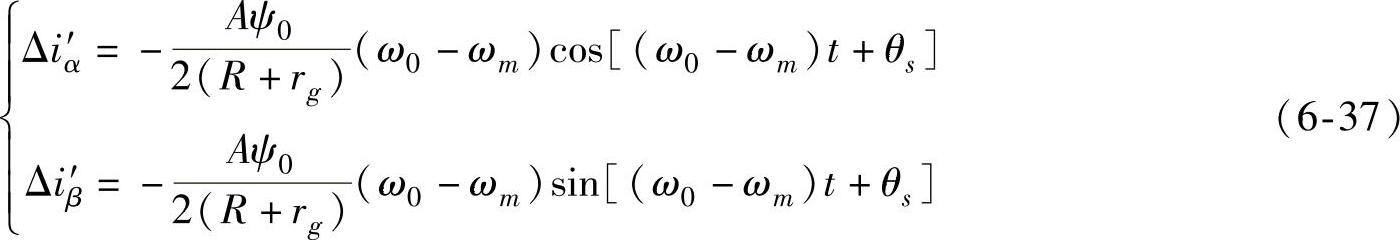(www.xing528.com)

假定Δψ_d≈0，Δψ_q≈0，则发电机电磁功率增量可以近似表示为

由图6-30可知，αβ坐标系与dq旋转坐标系的变换关系为

式中，。将式（6-39）线性化后代入式（6-38）中可以得到：

将式（6-37）代入式（6-40）中，简化为ΔT_e=K_eΔθ+D_eΔω形式，从而可以得到近似的电气阻尼系数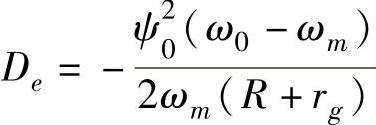。由此可见，在未接入STATCOM时，当发电机轴系的扰动频率与系统的谐振频率互补时，系统呈现负阻尼^[18，19]。

2.STATCOM接入系统引入的电气阻尼系数

当在发电机端口接入用于抑制次同步振荡的STATCOM时，与利用SVC抑制次同步振荡的机理分析相同，系统经线性化处理以后，STATCOM仍然可以等效为一个按照一定控制方式作用的次同步及超同步频率的电流源，此时利用叠加定理不考虑发电机引起的次同步电动势的作用，其等效电路结构如图6-31所示。

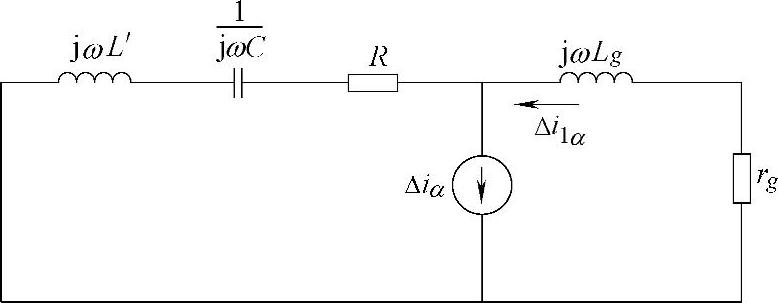
图6-31 机端并联STATCOM的系统结构图

根据式（6-35）可以得到，在αβ坐标系下由STATCOM产生的次同步及超同步电流分量为

由于STATCOM并联接入发电机端，其产生的次同步和超同步电流经分流后，一部分进入发电机，另一部分则流入电网。其中，按照图6-31所示的电流参考方向，发电机侧的次同步及超同步电流为

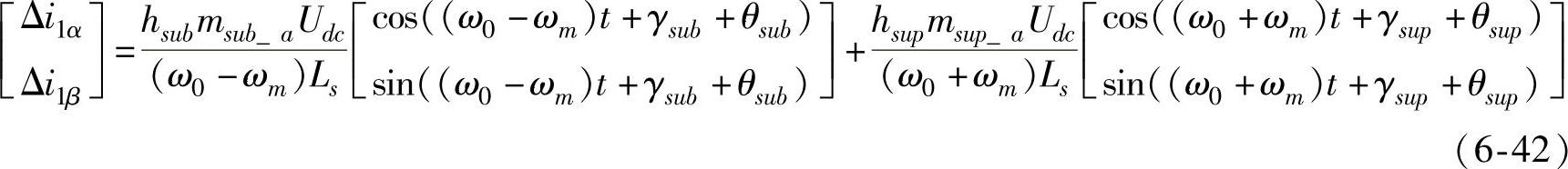
式中，h_sub与h_sup分别为次同步及超同步电流在发电机侧的分流系数；θ_sub与θ_sup分别为次同步及超同步电流分流后产生的相位偏移。

将式（6-42）代入式（6-40）中，经整理后仍可简化为ΔT_e=K_eΔθ+D_eΔω的形式，从而可以得到由STATCOM接入系统后引入的电气阻尼系数为

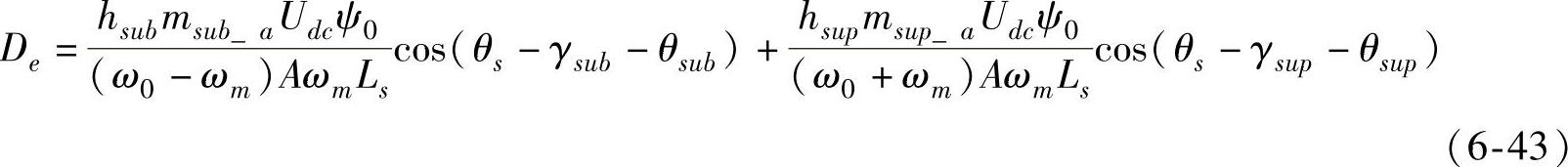
在式（6-43）中，γ_sub与γ_sup包含可控变量，通过采用适当的控制策略可以使得STAT-COM产生正的电气阻尼。对于如图6-31所示的串补引起的次同步谐振问题，由于系统中存在次同步频率下的谐振回路，通常STATCOM注入系统的次同步电流一般要远大于超同步电流，因此可以仅考虑次同步电流产生的阻尼特性，此时通过控制器设计仅需要满足θ_s-γ_sub-θ_sub=0，即可产生较大的正阻尼。

对于无谐振回路的次同步振荡问题（如由HVDC引起的SSO），进入系统的次同步及超同步电流相差不大，因此需同时考虑两者的阻尼能力。若所采用的控制策略使得γ_sub与γ_sup相互独立时，次同步及超同步电流可各自产生最大的正阻尼，即满足：

如果采用的控制策略使得γ_sub与γ_sup并不相互独立时，式（6-43）计算的次同步和超同步电流产生的电气阻尼之和存在一个正的最大值，即满足：

θ_s-β=0 （6-45）

式中，；。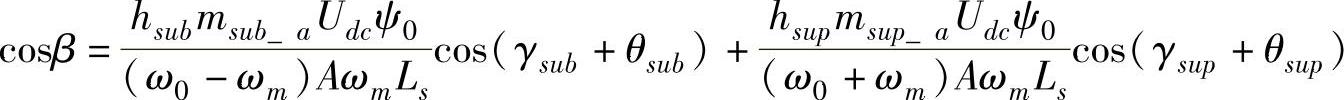

此外，由式（6-43）还可以看出，满足上述相位条件后，STATCOM提供给系统的正阻尼的大小主要受到以下几个因素的影响：

1）变压器漏抗（L_s）。STATCOM通过连接变压器接入系统，连接变压器的漏抗越小，STATCOM输出的次同步电流的变化率越大，抑制次同步振荡的响应速度越快。

2）分流系数（h_sub及h_sup）。在其他参数不变的情况下，系统侧的阻抗越大，由STAT-COM产生的次同步电流分量流入到发电机定子绕组的部分就越大，因此产生的抑制次同步振荡的阻尼转矩就越大。

3）STATCOM的直流电压（U_dc）及控制器参数（m_{sub_a}及m_{sup_a}）。直流电压U_dc与次同步及超同步分量的幅值调制率m_{sub_a}及m_{sup_a}决定了STATCOM输出电压次同步及超同步分量的幅值，从而决定了STATCOM注入系统的次同步及超同步电流的大小。

由式（6-35）可知，STATCOM所产生的电流中除了含有抑制次同步振荡所需要的次同步及超同步分量Δi外，还包含有基波分量i₁。从i₁的表达式中可以看出，在理想条件下，适当的调整参数，可以使得这部分基波分量值为零，从而使得STATCOM在没有发生次同步振荡时处于零功率输出状态。但在实际中，为了补偿控制器的开关损耗，维持直流侧的电容电压，同时由于高次谐波的存在，系统必须向STATCOM提供一定的功率消耗，与SVC在稳态下的运行状态相比，这部分功率很小。因此当系统中没有发生次同步振荡时，可以通过调节使得STATCOM输出的基波电压的幅值接近其接入点的系统电压幅值，这样在系统和STATCOM的连接线上只存在系统提供极少的功率以补偿开关产生的损耗，以及由STATCOM产生的谐波功率。

当系统发生次同步振荡时，将含有对应转矩扭振频率的信号作为STATCOM控制器的输入信号，控制器产生与转矩扭振频率相关的三相调制波信号，通过三角波载波调制，在换流器的输出侧产生与调制波频率相同的三相次同步及超同步电压分量，从而产生阻尼系统次同步振荡的次同步及超同步电流。