阻尼控制策略：抑制SSO

6.2.3.1 控制器设计

上节采用机端接入方式分析了SVC抑制次同步振荡的电纳调制原理。尽管这种接入方式在理论上能够起到最佳的次同步振荡阻尼效果，但是从工程实施的角度来看，由于SVC占地面积较大，在电厂内并联于发电机出口母线会给施工安装带来不便。因此，比较好的技术经济方案是将SVC通过已有的专用升压变压器连接于发电机组主变压器的高压侧，实际上SVC的安装地点选择在了电厂外。理论上，采用这种连接方式时，由于发电机组的主升压变压器的漏抗增大了SVC与发电机之间的阻抗，使得SVC产生的次同步频率电流更多地流向系统，在一定程度上降低了其抑制效果。但是工程经验表明，这种联接方式带来的系统整体安全性能更好，同时其抑制效果并没有受到严重的影响^[6-8]。因此，根据上述分析并结合国内工程实际，本节针对IEEE次同步谐振第一标准模型，采用在发电机组主变压器高压侧接入的方式，分析SVC抑制次同步振荡的控制策略，系统接线如图6-6所示。

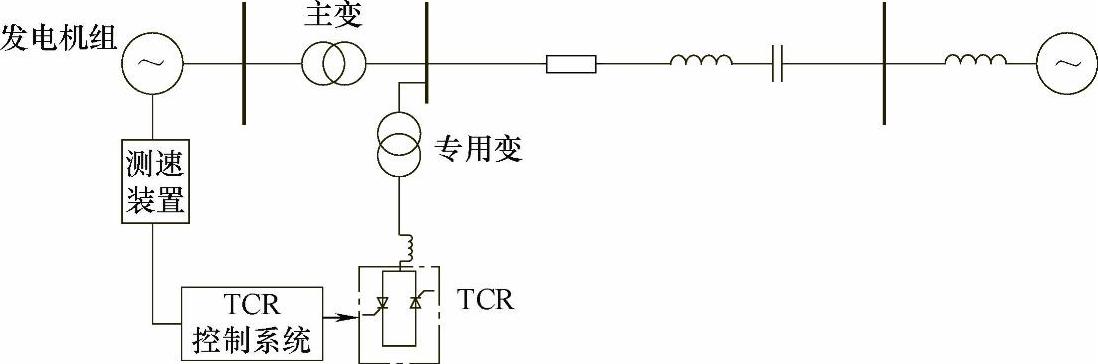
图6-6 SVC抑制IEEE第一标准模型主接线

由SVC抑制次同步振荡的原理分析得到，SVC的主要部件TCR需要产生与发电机转子自然扭振频率互补的次同步频率电流，而该次同步频率电流的相位应该与发电机转子转速偏差的相位相反。当发电机转速增加时，TCR中的无功电流减小，即TCR吸收的无功功率减小，则发电机端电压上升，发电机电磁功率增加，对于恒定的原动机机械功率，电磁功率的增加将导致转子动能的减小，最终使得发电机转子转速下降。相反地，当发电机转子转速减小时，TCR中的无功电流增加，使得发电机转子转动加速。此时能够在一定的SVC容量下，给发电机提供最大的阻尼转矩。按照这样的控制策略设计的SVC控制系统如图6-7所示。

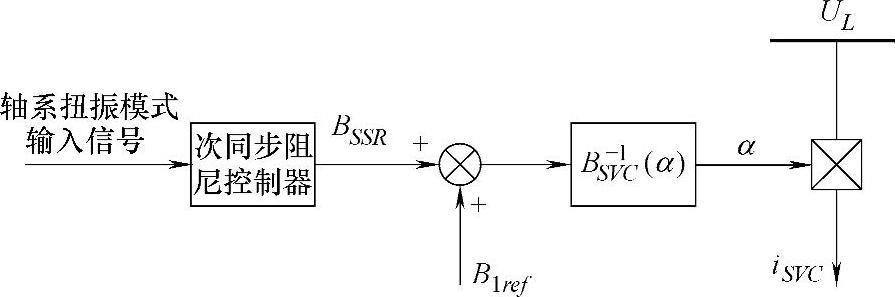
图6-7 SVC次同步频率阻尼控制器结构

SVC控制系统的输入信号可以选取含有原动机扭振模式分量的检测量，如发电机的转速偏差、输出功率、高压缸速度偏差等。通过次同步阻尼控制器形成满足上述控制要求的次频电纳控制量B_SSR，与稳态电纳参考值叠加后，根据等效电纳与触发延迟角之间的非线性关系，形成控制TCR晶闸管导通的触发延迟角α，从而产生用于抑制次同步振荡的次同步电流。

直接以发电机转速偏差作为控制器的输入信号可以确保对系统次同步振荡的抑制效果，但该方式下，各模态不能够得到各自最佳的相位补偿角度，造成SVC的抑制效果对控制器的相移更加敏感。这一问题可以采用模态控制技术加以解决，即将发电机转速偏差信号中对应各个扭振模态的频率分量分离出来，仅用其中不稳定的分量作为控制器的输入信号，使得SVC既可以抑制发电机组的扭振，又可以避免削弱系统与电气模式相关的阻尼。图6-7中的SVC次同步阻尼控制器的结构如图6-8所示。

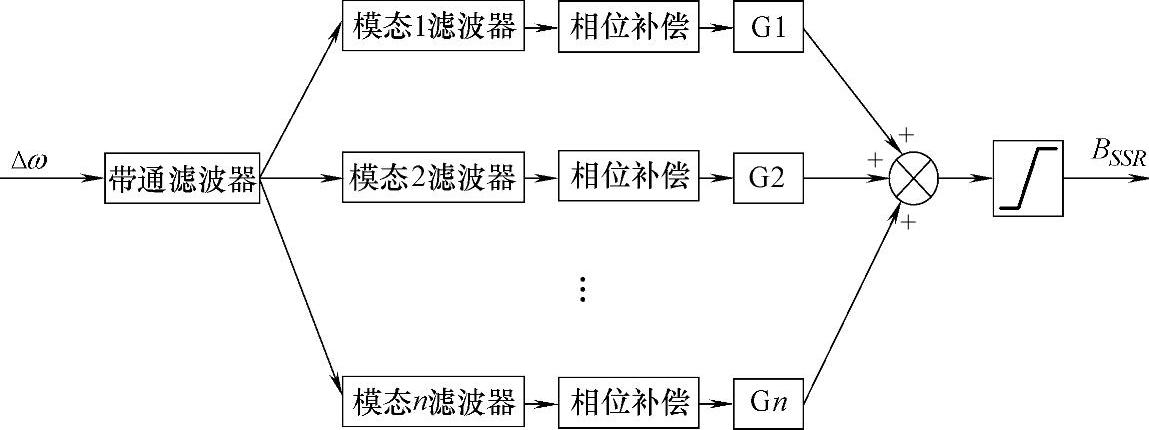
图6-8 SVC次同步阻尼控制器

图6-8中，SVC次同步阻尼控制器的输入信号为发电机的转速偏差。发电机的转速通过安装在其尾部的转速探头获取。转速探头采用磁阻传感器，其具有较高的磁场检测灵敏度，可以测量微弱的磁场，因此在测量发电机转速时具有很高的测量精度。为了尽量减小误差，转速转换箱将含有模态分量信息的发电机原始转速信号转换为高频信号（12MHz），然后通过测频法来计算转速偏差。

转速偏差首先经过一个有高通和低通滤波器串联而成的带通滤波器，它滤除了输入信号中的直流、低频和高频信号。模态滤波器按照待研发电机组次同步扭振模态的数目设计相应数目的独立模态控制通道，对每个模态设计的滤波器是窄带型带通滤波器，这样可以使得各个模态间的信号相互独立。通过模态滤波器获得各振荡模态的振荡分量，并对其进行相位补偿和比例放大，得到对应模态的控制信号，各控制信号相加并限幅后形成总的控制信号B_SSR。如上所述，该信号作为SVC稳态工作点电纳值的一个叠加量，一起作为SVC的电纳参考值调制SVC的基波电纳，产生与输入信号模态频率互补的次同步频率电流分量，进而在发电机中形成抑制该模态扭振的阻尼转矩。

在SVC的底层控制方面，按照TCR的整体结构，可以采用三个桥臂同相触发，也可采用三个桥臂分相独立触发，即每相各自针对其不同的参考电抗分别求解触发延迟角，这样求得的abc三相触发延迟角相互独立，虽然这种触发控制方式会导致三相不平衡，但能够更快地反映每相电抗的变化，理论上能够在更短的时间内抑制住发电机组的次同步扭振。同时，对于每相的两个反并联晶闸管的触发控制，可以采用对称的触发方式，即相邻两个正负半波的触发延迟角相位强制相差180°，也可以采用同相反并联晶闸管独立触发控制方式，即晶闸管按照本半波的参考电抗值求解其触发延迟角，并不强制同相晶闸管的触发延迟相位相差180°，这种触发方式可能会产生直流分量引起滤波器与专用变压器的铁磁谐振，但是它能够更快地跟踪扭振模态信号的变化，理论上具有更好的抑制效果。

6.2.3.2 抑制装置的最大容量估算

用于抑制次同步振荡的SVC容量是系统设计的一个重要方面，国内外较多的文献从理论上分析了SVC抑制SSO的可行性，以简单的故障验证了理论的正确性，但并没有考虑SVC的容量对其抑制效果的影响。发电机转速振荡的幅值随系统故障的不同而不同，当系统发生大扰动时，如机端接地短路故障，发电机转子的转速偏差初始幅值会大大超过设计容量不足的SVC产生的次同步频率电流能够抑制的最大振荡幅值，此时SVC不能有效地阻尼次同步振荡。为此提出，用于抑制SSO的SVC容量的计算需要按照轴系各部分能承受三倍其额定转矩的标准来计算，具体计算公式如下：

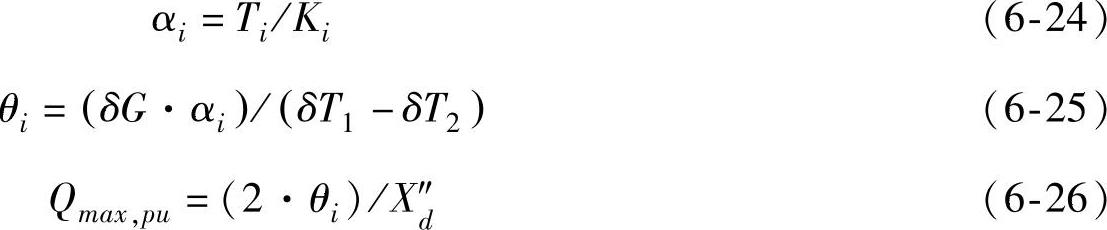
式中，α_i、T_i、K_i分别为发电机组轴系第i段质量块的最大角位移、所能承受的最大机械转矩和弹性系数；θ_i为发电机质量块所允许的最大转速偏差；δG、δT₁、δT₂为发电机质量块、轴系第i段质量块两端的振型角位移；X″_d为发电机的次暂态电抗；Q_max，pu是以发电机额定容量为基准的SVC最大容量估算值的标幺值^[9]。(www.xing528.com)

有学者研究认为，在确定了SVC的容量后，如图6-8所示的SVC次同步阻尼控制器的模态比例放大倍数就可以在综合考虑到容量限制、控制信号限幅要求、抑制SSR阻尼需求的因素下设定各个模态的增益。因此，模态增益按照在所有方式和扰动下提供足够阻尼且在最严重故障方式下使控制信号输出的限幅时间小于5s的设定标准进行整定，这样既保证了在小扰动下能获得较好的阻尼，在大扰动下输出限幅时间不至于太久，从而提高抑制SSR的效率^[10]。

以IEEE第一标准模型的发电机组为例，计算用于抑制该系统次同步谐振的SVC的容量。已知发电机的额定容量为892.4MVA，机械转矩的基准值为2.3672×10⁶N·m，汽轮机轴系分为HP、IP、LPA、LPB四个集中质量块，机械功率入/出比例分别为30%、26%、22%、22%，X″_d=0.135pu。轴系质量块最大角位移按照三倍的额定机械转矩来计算，由轴系参数可计算出各模态扭振振型如表6-1所示。根据以上参数，由式（6-24）计算得到轴系各质量块最大角位移如表6-2所示；由式（6-25）计算出各质量块允许的最大角位移则如表6-3所示。

表6-1 轴系各模态扭振振型

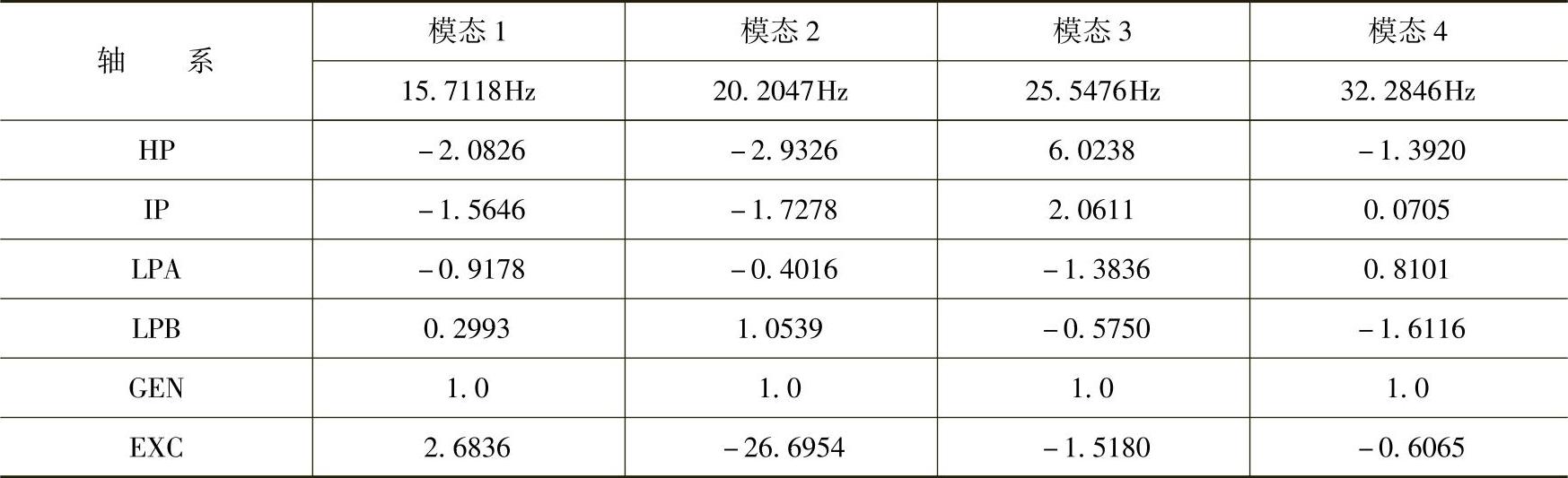
表6-2 最大角位移α_i

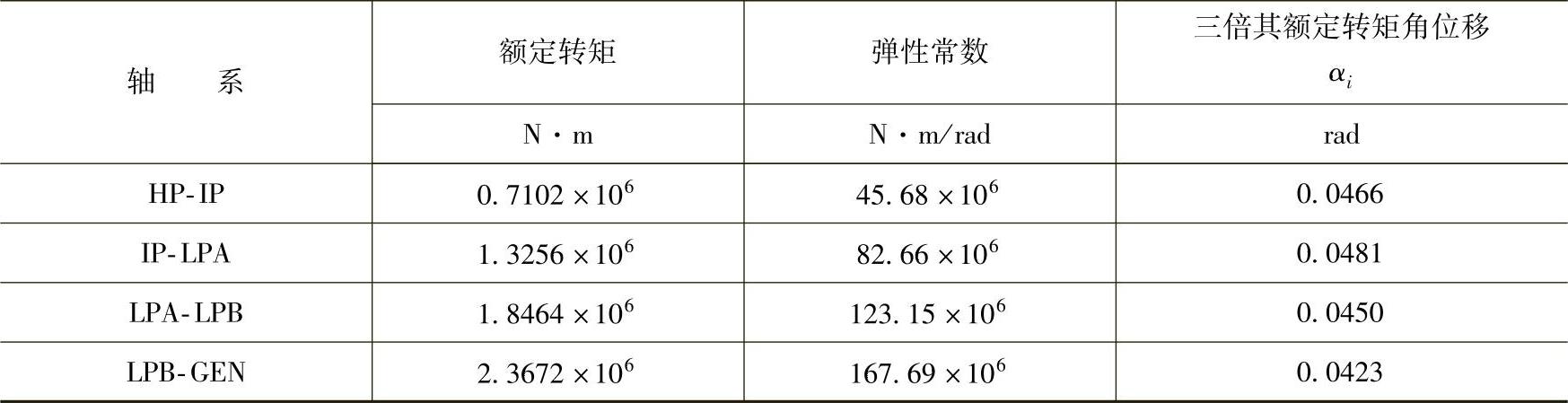
表6-3 发电机质量块最大转速偏差θ_i

对于IEEE第一标准模型系统而言，系统不稳定的次同步振荡模态为模态2（20.2047Hz）。由表6-3所示的发电机质量块的最大角位移可得LPA-LPB轴系上的θ_i最小，则根据式（6-26），要抑制该模态的次同步谐振问题，SVC的容量标幺值为

Q_max，pu=（2θ_i）/X″_d=2×0.0309/0.135=0.4578（pu）

SVC的容量是按照需要抑制的模态和所允许的振荡幅值进行计算的，且只是SSR抑制的一个暂态容量要求。对系统动态特性作进一步的研究可以优化SVC的容量。

6.2.3.3 SVC抑制效果仿真

以IEEE第一标准模型为例，TCR按照三相独立控制和反并联晶闸管非对称触发方式控制，SVC的容量按照上述计算的大小配置，其抑制效果如图6-9所示。

设定2s时系统在串联电容器后发生三相金属性接地故障，如果系统不采取任何抑制措施，发电机轴系扭振是发散的；如果投入SVC，则其能在6s内将发电机的轴系扭振抑制到较低的幅值。

当系统处于稳态运行时，设置触发延迟角使TCR吸收的感性无功功率与滤波器的容性无功功率相等，则装置对系统的潮流没有影响，也不会影响到系统的暂态稳定。在系统发生SSR时，次同步阻尼控制信号的限幅要求已经考虑了在暂态时SVC的容量限制，并且稳态运行的容量约为额定容量的一半，因此SVC产生的次同步电流分量不会超过与其匹配的专用变容量限制。

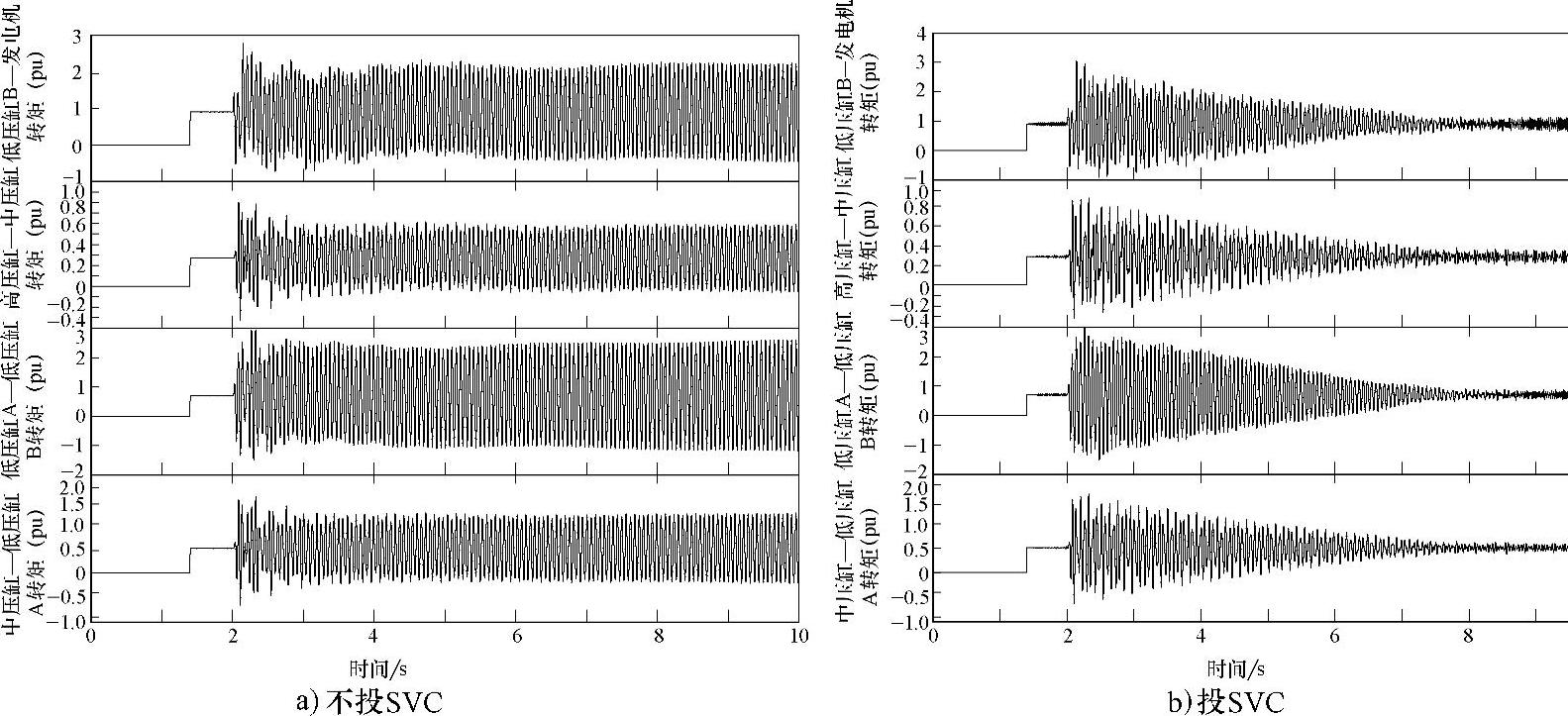
图6-9 SVC抑制SSR的仿真对比