自然抑制SSO的机理：探究与优化

利用TCSC抑制SSO一直是学术界和工程界重视的课题，国内外相关学者已做了大量的研究和试验。总的来说，TCSC抑制SSO有自然抑制和主动抑制两种方式。自然抑制是指通过适当的底层脉冲触发控制，改变TCSC在次同步频率下的阻抗特性，使TCSC阻抗在次同步频率下呈感性，阻断电气部分的谐振条件，进而破坏汽轮发电机轴系与线路串联电容器之间的相互作用。自然抑制方式只与TCSC的自身参数有关，不受系统运行条件的影响。

在国内、外相关研究文献的基础上，本节首先分析了TCSC次同步频率阻抗特性；然后，从TCSC次同步频率阻抗特性出发分析了TCSC自然抑制SSO的机理；最后，针对采用自然抑制的方式解决SSO问题时，TCSC主参数的设计原则进行了分析。

5.3.3.1 次同步频率阻抗特性

TCSC自然抑制SSO不受系统运行条件的影响，其固有的次同步频率阻抗特性决定了TCSC与SSO的相互作用机理。因此，正确分析TCSC次同步频率阻抗特性是研究TCSC自然抑制SSO能力以及进行TCSC参数设计的前提。目前，已有一些文献开展了关于TCSC的次同步频率阻抗特性的研究。

参考文献[11]在假设TCSC两端电压中工频分量和次同步频率分量能够解耦的条件下，采用在TCSC的基波电压上叠加一个微小的次同步频率电压分量，进而求取次同步频率阻抗的方法，得到了TCSC（C=40.104μF，L=25.1mH）在次同步频率为20Hz时的阻抗特性，如图5-11所示。

由图5-11可以看出，TCSC在次同步频率下（20Hz）等效为一个具有正实部的阻抗。当导通角比较小时，TCSC工作在容性区域，次同步频率下的等效电阻（简称次频电阻）的数值也比较小；随着导通角开始增大，TCSC的次同步频率下的等效电抗（简称次频电抗）呈容性，且将缓慢减小，而次频电阻将增大；当导通角增大到一定程度时，TCSC次频电阻达到最大值，此时次频电抗随导通角变化而显著变化，即调节导通角可以显著改变TCSC的次频电抗。如果导通角继续增大，TCSC将进入感性区域，这时表现为一个较小的感抗，同时次频电阻将减小，在感性区域中，TCSC次频电抗和工频电抗都很小。

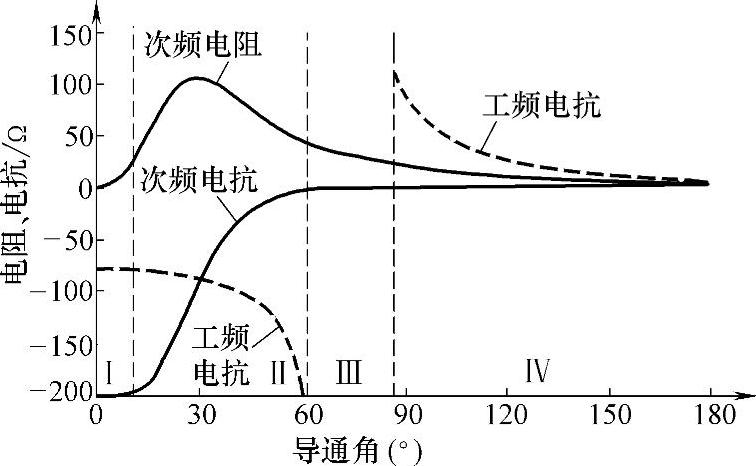
图5-11 TCSC次频阻抗特性曲线（20Hz）

根据TCSC的次同步频率下阻抗变化趋势，将TCSC工作点范围划分为如图5-11所示的4个区域（即区域Ⅰ，Ⅱ，Ⅲ，Ⅳ）。区域Ⅰ内次频电阻小，次频电抗呈容抗且数值几乎没有发生改变，此时TCSC类似于FSC；区域Ⅱ内次频电阻效应作用显著，同时次频容性电抗急剧减小；区域Ⅲ内将发生工频谐振；区域Ⅳ内电感效应作用显著。可见，TCSC在次同步频率下的等效电抗也随着导通角的增大而由容性过渡到感性，在次同步频率下的等效电阻呈现正值，而在工频下则为0；同时TCSC在次频电抗下进入感性区域更早，其电抗特性不存在以电抗急剧变化为特征的失稳区域，在次频容性区域内容性电抗随导通角增大而减小，这一点和它的工频特性恰恰相反。

图5-11为单一次同步频率下（20Hz）TCSC的次同步频率阻抗特性曲线，而参考文献[12]基于TCSC的电路拓扑采用了研究稳态频率响应特性的数学方法，绘制当次同步频率f_s和导通角σ变化时TCSC（TCSC配置为C=47.34mF，L=23.78mH）的三维次同步频率阻抗特性图，如图5-12所示。采用TCSC的小信号二阶动态TCSC线性化模型，参考文献[13]得到了次同步频率阻抗特性的表达式，对此进行研究后绘制了次同步频率阻抗的三维特性图，其变化趋势与图5-12基本一致。

针对TCSC的次同步频率阻抗特性的研究，参考文献[11-13]给出的结论基本一致。现结合图5-12总结如下：

1）对应于0°～20°左右的导通角之间，次频电抗存在一个容性曲面，呈容性；导通角超过20°时，次频电抗均表现为感性。

2）对于某一特定的次同步频率，其次频电抗存在一个临界导通角σ_c。在导通角较小时，随导通角的增加，次频电抗增加的幅度很小；当逐渐接近σ_c时，次频电抗对导通角变化的灵敏度增大，其值也迅速增大；当达到了σ_c时，次频电抗由容性转化为感性，并随导通角的增大而感性增大。

3）次频电抗特性容性区域和感性区域过渡较为光滑，不像工频基波阻抗特性那样存在显著谐振区域。

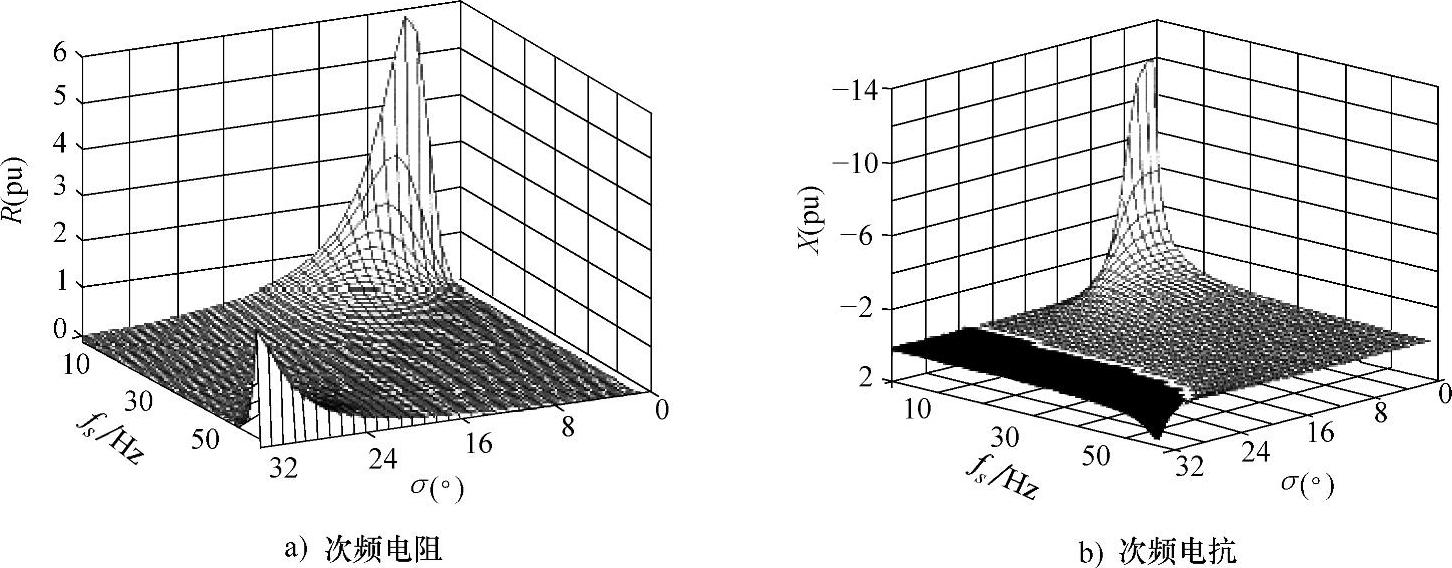
图5-12 TCSC次同步频率阻抗特性

4）在导通角为0°～32°区间内，次频电阻为正值，有助于对电气谐振能量的消耗，减少振荡的幅值和发散速度，能在一定程度上缓解SSO。

需要注意到参考文献[14-16]的研究结果与上述结论却存在一定的差异。基于数字仿真实现的测试信号法，参考文献[14]研究结果表明，TCSC次频电抗呈现感性，从而破坏了发生SSO的条件。参考文献[15]中ABB公司提出了同步电压翻转（Synchronous Voltage Reversal，SVR）的晶闸管底层控制策略，解析地推导出视在阻抗与次同步频率的解析表达式，认为晶闸管工频触发导通对次同步频率电气量的调制使TCSC的次频电抗在低于工频的所有频率下均为感性。参考文献[16]中，GE公司通过数字仿真和暂态网络分析试验和现场测试，表明TCSC对SSO呈“中性”，即次频电抗为零，但没有进行理论分析。显然参考文献[14-16]与图5-12结论不完全一致。

由此可见，目前已取得研究成果中关于TCSC的次同步频率阻抗特性的研究存在着显著差异甚至对立的情况。究其原因，一方面在于TCSC次同步频率阻抗特性较为复杂；另一方面在于目前已有文献中采用的TCSC数学模型和分析方法各不相同，并且在分析过程中都进行了不同程度的简化处理，因而造成研究结果存在一定的差别。因此，TCSC的次同步频率阻抗特性还有待进一步的深入分析。

5.3.3.2 TCSC自然抑制SSO的机理分析

目前关于TCSC自然抑制SSO的机理大致可以归结为电阻性机理、电感性机理和电阻-电感综合作用机理。

1.电阻性机理

参考文献[17]认为TCSC次频电阻将向系统提供正阻尼；只有当次频电阻值足够大时，其提供的正阻尼才能完全抵消系统SSO引入的电气负阻尼。由图5-11可以看出，TCSC只有在导通角较适中时次频电阻幅值较大，太小或者太大时对应的次频电阻幅值均不大，因此此时在导通角太小或者太大情况下系统存在发生SSO的可能。但是，仿真分析和工程实践表明^[16]：工作在大导通角下，TCSC能够很好地抑制SSO；而工作在小导通角下也有可能有效。采用电阻性机理，不能解释这种现象。

2.电感性机理

电感性机理认为，只有在TCSC次频电抗呈现为感性时，TCSC和线路电抗才不存在发生电气谐振的可能，进而破坏系统发生SSO的条件。根据此观点，由图5-12可知，当导通角比较大时，TCSC的次频电抗呈感性，系统不存在发生SSO的可能；而导通角较小时，次频电抗呈容性，系统可能发生SSO。这和小导通角下系统也有可能保持稳定的实际情况是不一致的^[16]。

可见，利用电阻性机理和电感性机理都不能充分解释TCSC抑制SSO的机理，这在于两者都只重视了TCSC在次同步频率下的次频电阻或次频电感的调制效应，没有综合考虑两者的作用。

3.电感-电阻综合作用机理

参考文献[11，14，18]指出，在分析TCSC抑制SSO的机理时，必须全面考虑TCSC在次同步频率下的电阻-电感综合作用。参考文献[18]中通过理论和仿真研究表明，TCSC的次频电抗特性对SSO的抑制起着主导作用，当次频电抗呈感性时，破坏系统发生SSO的谐振条件，能够彻底地消除SSO；当次频电抗呈容性时，系统存在发生SSO的可能，但由于此时导通角小幅变动就会引起次频电抗的较大变化，使得TCSC次频电抗偏离谐振点，因此也能在一定程度上抑制SSO。TCSC的次频电阻对SSO的抑制作用本质上是一个能量转换的过程，即将次同步能量转换为等效工频能量，并不能破坏SSO的谐振条件，只能起到减小振荡幅度和发散速度的阻尼作用特性，因此它只能在一定程度上抑制SSO的发生，不可能彻底消除SSO。

电阻-电感综合作用机理本质上充分揭示了TCSC抑制SSO的机理，对仿真和工程实际中的现象给出了合理的解释。基于此，结合图5-11中TCSC的次频阻抗特性，对TCSC抑制SSO能力与导通角的关系进行分析。

1）区域Ⅰ属于容性区域。TCSC次同步等效电抗呈容性且几乎不变，因此此时是引发SSO的危险区域。如果TCSC的固定电容调谐到某一不稳模态，即次频谐振工作点落在区域Ⅰ中，则在此区域中时很难避免SSO的发生。但此时由于TCSC次频电阻呈现正值，与次同步频率下等容抗值的FSC相比，TCSC还是能够在一定程度上抑制SSO。如果TCSC没有调谐到任何模态，并且其电容值远离任何模态的调谐值，则系统不会发生SSO。(www.xing528.com)

2）区域Ⅱ属于容性区域。此时，TCSC次频电抗呈容性，具备激发SSO条件。但此时，次频电抗曲线斜率较大，等效容抗随着导通角改变而显著变化，有助于破坏系统次频振荡条件。另外，此时次同步等效电阻幅值较大，能够提供较大的阻尼。因此，如果次频谐振点落在此区域中，则除了该谐振点附近的工作点外，其他工作点处发生SSO的可能性也很小。如果该次频谐振点不在此区域中，则所有工作点处都能保证系统SSO稳定。

3）在区域Ⅲ中，TCSC工频工况将失去稳定，从而导致系统发生工频谐振。但是，由于此时TCSC的次频电阻仍然比较大，次频电抗开始转变为感性，因此系统次频工况将仍然保持稳定。

4）区域Ⅳ属于感性区域，此时次频电抗处于感性区域，不可能与线路感性电抗发生SSO，加之在此区域中次频电阻的作用，TCSC此时能有效地抑制SSO。但是由于TCSC运行在此区域时将导致线路损耗增加，输送能力下降，因此其只能作为一种应急措施使用^[11]。

由上述分析可知，TCSC自然抑制SSO的机理可以用电阻-电感综合作用的机理来解释，其对SSO是否具有抑制作用取决于其次同步频率下的阻抗特性。此外，结合图5-12分析表明，TCSC能否抑制SSO与导通角等参数紧密相关，但与次同步频率下具有等效容抗的FSC相比，由于TCSC的次频电阻效应的存在，因此抑制效果要好于FSC。除此之外，TCSC自然抑制SSO的能力还与其控制器的优劣、触发算法等紧密相关。因此，TCSC对SSO的自然抑制是有条件的，工程中应结合实际情况具体分析。

5.3.3.3 自然抑制条件下TCSC的设计

由前文分析可知，TCSC对SSO的抑制能力与其导通角σ紧密相关，因此，有必要研究如何选择合理的TCSC主电路参数，使得TCSC运行时能够通过控制σ的大小避开SSO的危险区，进而充分发挥TCSC自然抑制SSO的作用。TCSC的主电路参数设计主要是确定合适的k值。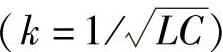

k值的大小取决于电容C和电感参数L的选择。电容参数主要是根据系统运行对串联补偿度的要求来确定。由前文分析可知，TCSC并联电容器的选择不仅要考虑满足工频基波阻抗调整的要求，同时要尽可能地避开SSO的危险区。当串联电容器确定之后，电感参数的选择即是如何选择合适的k值。首先考虑工频调节特性的要求。对于任意k值，当σ由0°变到90°时，TCSC工频特性有可能出现多个谐振点，而限制k≤3就可以达到当σ在0°～90°之间只出现一个容性感抗区域和感性感抗区域。当k值较大时，容性范围会减少，这给TCSC在高容抗下的调节带来困难，严重时可造成装置运行的不稳定；而从保护TCSC安全和减小MOV的损耗出发则希望k值取较小值。从抑制SSO的观点来看，不同的k值选择会引起感性区域范围大小的变化。图5-13给出了不同k值下频率与临界导通角的关系。对于一定的σ值，次同步频率增大时，σ随之增大，感性区域减小。当k增大，σ减小时，将扩大低频视在阻抗的感性区域，有利于SSO的抑制。

综上所述，为满足工频基波阻抗调节特性的要求，希望k取较小值，而为了增强TCSC自然抑制SSO的能力，希望k取较大值。通过仿真分析，k值最好在2.3～2.7范围内折中选择^[12]。

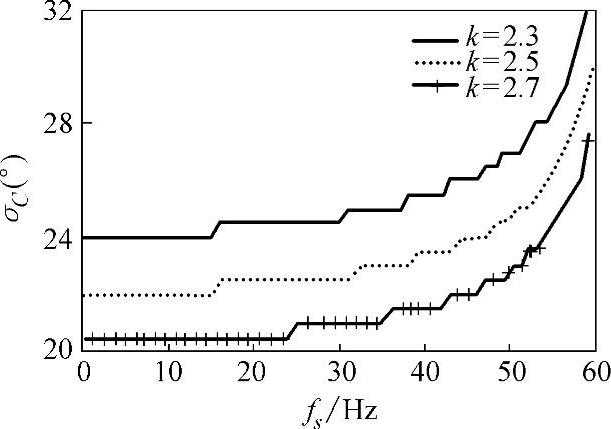
图5-13 不同k值下频率与临界导通角的关系

5.3.3.4 自然抑制的几种触发算法

目前世界上，由SIMENS公司、ABB公司、GE公司以及中国电力科学研究院等设计投运的TCSC装置均采用自然抑制这种方式解决SSO问题，但其采用的脉冲触发算法各不相同。ABB公司采用的是同步电压翻转（SVR）触发算法，并成功应用于瑞典的Stöde工程；GE公司和SIMENS公司采用的是调整触发延迟角的算法；中国电力科学研究院结合伊冯串联补偿工程采用的TCSC的研究，提出了电容电压增量控制算法。另外，参考文献[19]提出了控制电压过零点的SSO控制算法，并从理论上分析了其可行性。

以下介绍几种典型的具有抑制SSO功能的脉冲触发算法。

1.同步电压翻转触发算法

SVR触发算法是由Lennart Ängquist首先提出的一种TCSC底层触发算法，并由ABB公司成功应用于工程中。

TCSC容性模式下稳态运行时，其线电流I_L、电容电压U_C及阀电流I_V的相对相位关系如图5-14所示。对比I_L和I_V可见，晶闸管导通时间远远小于系统频率半波时间，且出现在线路电流I_L峰值附近，因此可认为在晶闸管导通期间，I_L近似维持恒定值。基于此假设，可以认为晶闸管导通期间，I_V使电容电压U_C迅速反向极化，U_C在晶闸管导通时间间隔的中间发生瞬时极性翻转。稳态时U_C在晶闸管导通开始和截止瞬间大小相等、方向相反，因此晶闸管的触发导通对U_C的影响可以表示为等距离瞬时翻转。大小相等、方向相反，因此晶闸管的触发导通对电容电压的影响可以表示为等距离瞬时翻转。这种瞬时极性翻转引起U_C的平移提升，稳态时U_C平移提升的绝对值为U_C增量绝对值的2倍。电容电压的过零点发生在线路电流峰值时刻，称作同步电压翻转时刻。

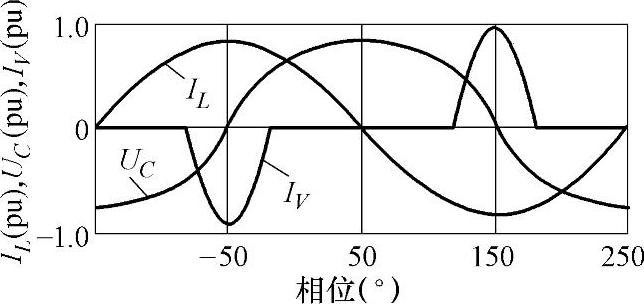
图5-14 容性模式下TCSC的波形

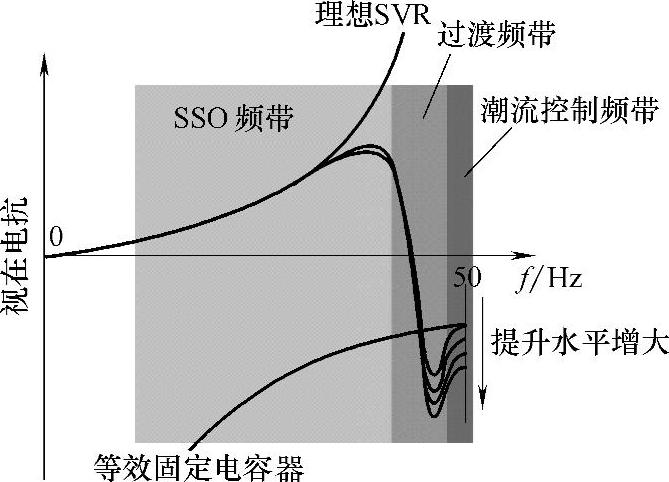
图5-15 采用SVR的TCSC次频电抗特性

当发生SSO时，系统中存在次同步频率分量，此时U_C过零点时刻相对于同步电压翻转时刻具有一定的相位移，引起U_C不再是等距离极性翻转。SVR触发算法的目的即是控制U_C的过零时刻，使之发生在同步电压翻转时刻，从而控制U_C极性翻转前后的平移提升值，消除次同步频率分量对U_C极性翻转前后平移提升值的影响，达到抑制SSO目的。

参考文献[20]对采用SVR触发控制的TC-SC的次频电抗进行了研究，如图5-15所示。可以看出，次同步频率范围内，TCSC的阻抗外特性表现为感性，因此若系统单独使用TCSC作为补偿措施时，破坏了系统的谐振条件，因此会在在一定程度上抑制SSO。

2.电容电压增量控制算法

参考文献[21]根据TCSC的数学模型，研究了电容电压增量的特点，提出了电容电压增量控制算法。

在线路电流不变的条件下，TCSC处于感性连续调节或容性连续调节状态时，其电容电压与TCSC始终处于晶闸管关断状态时的电容电压的差值，定义为电容电压增量。稳态时，TCSC电容电压增量与其工频电抗基本呈线性关系。由于电容电压增量对应微调时TCSC工频电抗的增加，因此对TCSC的阻抗控制可以转化为电容电压增量波形的控制，避免了因使用触发延迟角作控制变量而引起TCSC固有非线性特性所带来的问题。

电容电压增量控制触发的控制目标主要是通过对电容电压增量幅值的控制，满足电力系统对TCSC阻抗控制的要求。而当系统中发生SSO时，由于电容电压中次同步分量的作用，电容电压增量将会增加或减少，波形的对称性也遭到破坏。该算法通过控制每个正负半周电容电压增量，在实现TCSC基波阻抗控制的同时，快速调制TCSC上的多余电荷，使电容电压波形与不发生SSO的电容电压波形尽量一致，因此维持了TCSC的基波阻抗；在控制电容电压增量的同时，通过调制电容器上的电压波形，使TCSC模块对次同步频率呈感性阻抗，起到抑制SSO的作用。

电容电压增量控制中的触发控制根据系统运行需要的TCSC命令阻抗和实测的线路电流，确定电容电压增量的命令值，再根据电容电压和线路电流的实时测量值计算出本半周晶闸管导通前的电容电压增量。两者结合计算确定触发延迟角，使晶闸管在相应时刻导通，当晶闸管导通过程结束后，实际电容电压增量等于电容电压增量的命令值。

参考文献[22]在IEEE第一基准模型上进行了TCSC抑制SSO的物理模拟试验。试验结果说明电容电压增量触发算法对SSO有明显的抑制作用，同时阻抗控制的响应速度也很快。