了解机电扭振相互作用机制

系统发生的任何冲击或扰动均可能在发电机转子上激发出振荡转矩，该电磁转矩一般含有从次同步到几倍于工频频率的单向衰减的、指数衰减的和振荡的转矩分量。当次同步频率电流进入发电机定子绕组就会产生相应的次同步频率的机端电压，该电压反过来将维持次同步电流，从而产生自激现象^[5]。如果这种自激只涉及发电机组转子的励磁绕组则称为异步发电机效应，如果自激现象同时涉及转子的电气部分和机械部分则出现机电扭振相互作用。

在发生次同步振荡时，机械系统与电气系统间的扭振相互作用远比异步发电机效应强烈和复杂。为便于分析，假设发电机转子上有一个频率为ω_m的小幅值扰动，则发电机的转速可以表示为

ω=ω₀+Asin（ω_mt） （4-30）

在αβ静止坐标系中，暂态电抗后的电动势e_α可以表示为

e_α=ωE′sin（ω₀t+δ） （4-31）

由发电机转子运动方程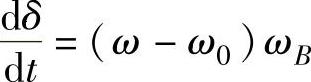可以得到发电机暂态电抗后的电动势的电压相角为

在次同步振荡的分析中，可以认为机电扭振相互作用时的轴系次同步扭振的幅值很小，发电机定子中感应的暂态电抗后的电动势e_α包括三个分量，除了工频电压外还存在与轴系扭振频率互补的次同步和超同步分量的电压。把式（4-30）代入式（4-31）可以得到电动势e_α的表达式为

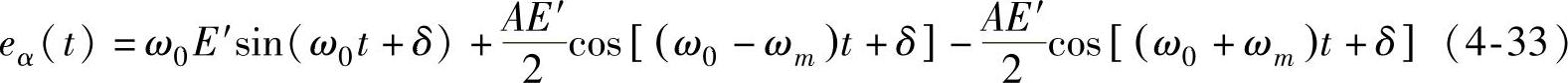
将式（4-32）代入式（4-33）进一步化简和变换可以得到e_α用三个分量和的表达式为

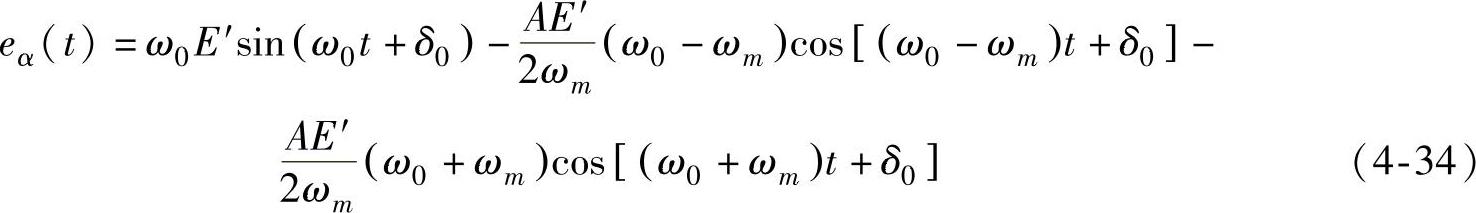
同理，可以推导出静止坐标系中β轴上的分量用三个频率分量之和的形式表示的暂态电抗后的电动势为

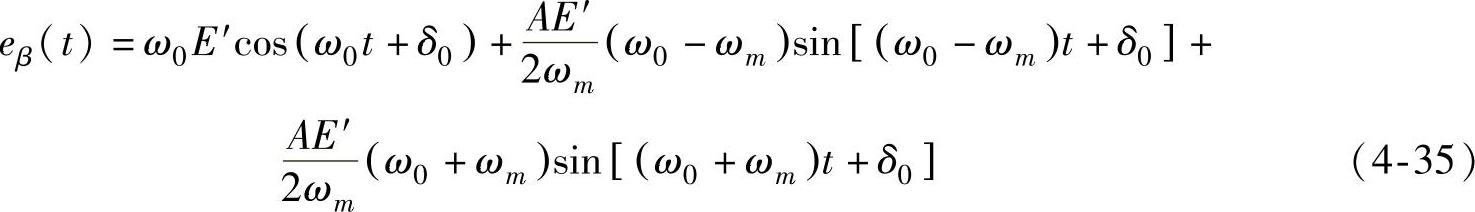
由式（4-34）和式（4-35）可以得到发电机暂态电抗后电动势的次同步分量的静止坐标系中表达式为

在静止坐标系中，电力网络部分流过的系统次同步频率电流则由次同步电动势和系统的次同步频率阻抗决定，

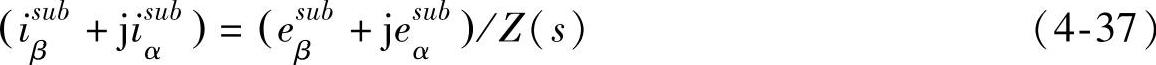
式中，，令s=j（ω₀-ω_m），则包括发电机次暂态电抗及外部电力网络部分的次同步频率的阻抗为(www.xing528.com)

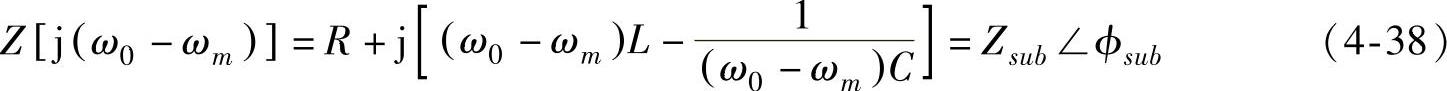
系统的谐振频率为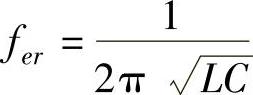，当由式（4-36）表示的发电机次同步电动势的频率（f₀-f_m）≈f_er，则式（4-38）中的次同步阻抗的电抗值非常小；当（f₀-f_m）＞f_er时，系统的次同步频率电抗为感性；反之，系统的次同步频率电抗为容性。由式（4-36）～式（4-38）可得

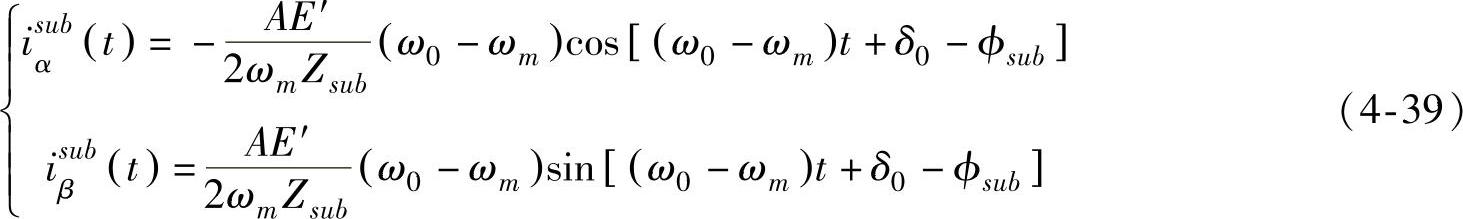
由静止坐标系αβ到旋转坐标系dq的变换关系

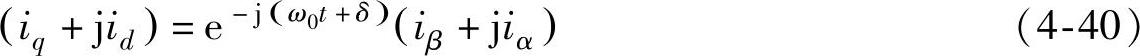
将式（4-39）代入式（4-40）可以得到系统的次同步频率电流的q轴分量为

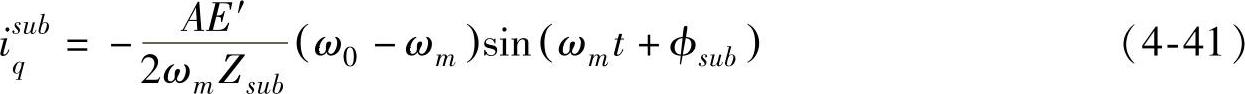
由式（4-41）表示的系统次同步频率电流分量在发电机中产生的次同步频率电磁转矩为

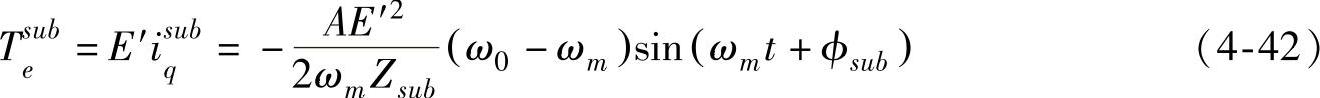
同理，对于系统的超同步分量阻抗Z_sup∠ϕ_sup，阻抗的模值比次同步阻抗大得多，其角度为正，在系统中表现为感性。由超同步电流产生的超同步电磁转矩为

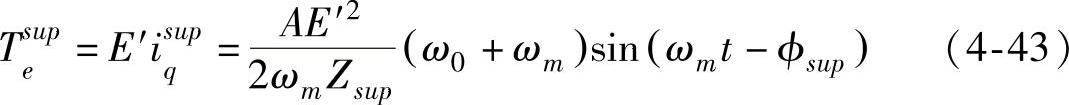
式（4-42）和式（4-43）表示由系统次同步、超同步电流产生的电磁转矩的频率均与发电机转子上扰动的频率相同，则电磁转矩阻尼系数为

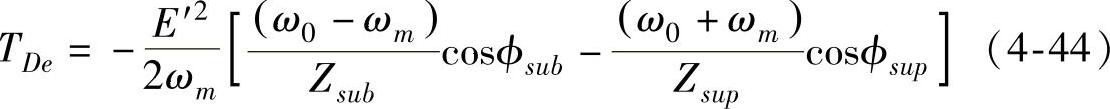
发电机转子上有次同步频率扰动时，由机电扭振相互作用产生的电磁转矩的阻尼系数用向量图表示，其关系如图4-7所示。

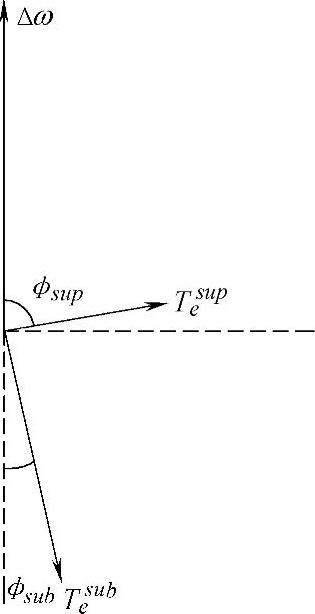
图4-7 发电机次同步阻尼转矩向量图

在串联补偿输电系统中，当发电机转子上的扭振频率与电网络谐振频率近似互补时f₀-f_m=f_er，电气部分的次同步和超同步的阻抗有Z_sub＜Z_sup且ϕ_sub≈0°，ϕ_sup≈90°。因此，系统次同步电气阻尼系数一般为负，发电机在扰动下将会发生该模态的次同步谐振^[4]。