轴系扭振稳定性研究

在有串联补偿的输电系统中，任何冲击或扰动均可能在发电机定子中引起次同步谐振电流，当该次同步频率电流在同步发电机内建立起旋转磁场时，该模态下的旋转磁场落后于转子的同步旋转磁场，转子将受到频率为f₀-f_er的交变电磁力矩。如果该交变电磁力矩的频率等于或接近于发电机组轴系的任何一个自然扭振频率时，则可能发生机电系统的次同步谐振。

对发电机轴系进行线性化处理，可以用RLC构成的一端口无源电路来进行计算，并与电网络部分结合组成一个闭合电路^[3，4]，如图4-6所示。

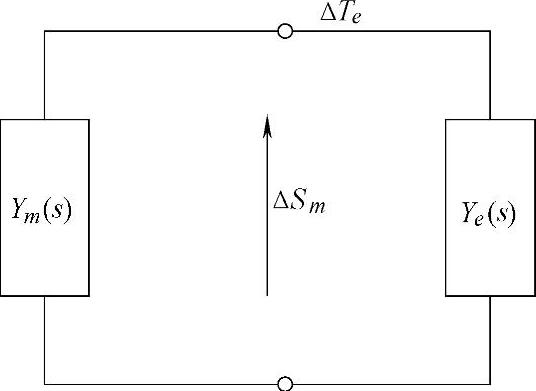
图4-6 机械部分与电气部分构成的整体

线性化的发电机组机械部分与电气部分构成的系统满足网络方程：

[Y_m（s）+Y_e（s）]·ΔS_m=0 （4-23）

式中，ΔS_m为发电机转差率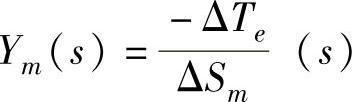；为机械部分的等效导纳函数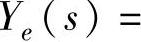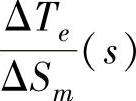；为电气部分的等效导纳函数。

系统的特征根满足方程Y_m（s）+Y_e（s）=0；对于系统的某一扭振模态ω_k，把s=jω_k带入式（4-23）就可得到系统扭振模态频率应该满足的方程式：

Y_m（jω_k）+Y_e（jω_k）=0 （4-24）

实际上，根据Y_e（s）的定义，Y_e（jω_k）也可以表示为

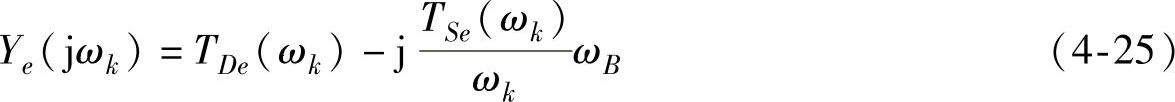(www.xing528.com)

式中，T_De和T_Se分别为发电机电磁转矩的阻尼转矩和同步转矩，是由发电机及外部电网络共同决定的。同样有

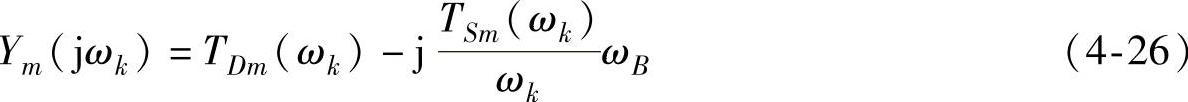
把式（4-25）和式（4-26）代入式（4-24）可以得到决定系统扭振频率的式（4-27），通常情况下，T_Se（ω_k）对T_S（ω_k）的过零点影响较小，因此扭振频率主要由T_Sm（ω_k）决定。

T_S（ω_k）=T_Sm（ω_k）+T_Se（ω_k）=0 （4-27）

确定系统在该扭振频率下是否失稳的判别式为

T_D（ω_k）=T_Dm（ω_k）+T_De（ω_k）＜0 （4-28）

如果由式（4-28）决定的扭振频率下的阻尼转矩小于零，则系统在该扭振频率下是不稳定的，这也是进行系统次同步振荡阻尼特性研究的依据。

式（4-28）等价于判断系统的扭振模式衰减指数为负，即系统模态净阻尼

σ=σ_m+σ_e＜0 （4-29）