电容器组接入位置选择原则及注意事项

本节论述串联补偿系统的稳态性能。对输电线路进行串联补偿时，串联电容器组的接入位置对系统的补偿效果有很大的影响，选择电容器组在输电线路接入位置时需要考虑如下几个因素：

1）作为电容器在线路位置上的函数，其“有效性”是变化的。

2）电容器位置影响输电线路的电压分布。

3）线路和电容器保护受电容器位置的影响。

4）不同位置时电容器组的可维护性。

5）如果电容器使用金属氧化物限压器保护，则限压器的通流能力要求随电容器位置而变化。

串联电容器可以安装在输电线路的任何位置，但是当超高压长距离输电线路两端还需要装设并联电抗器时，需要解决串联电容器和并联电抗器的相对位置。通常，多电容器组的串联补偿系统有如图4-3所示的四种接线方式^[2]。

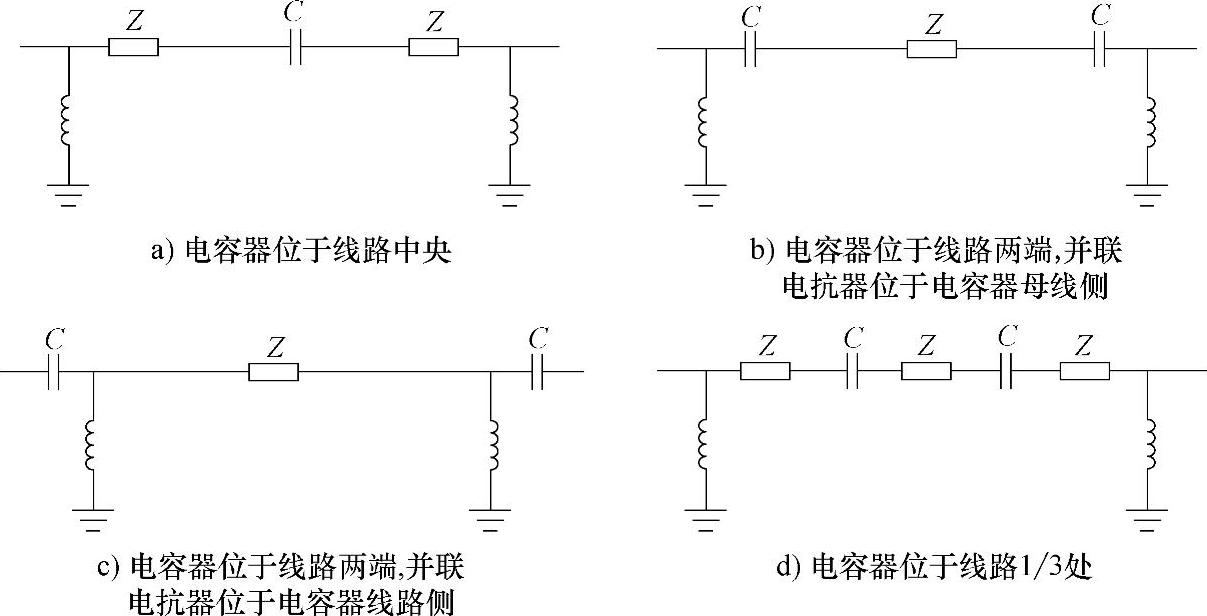
图4-3 串联电容器接入系统的典型位置

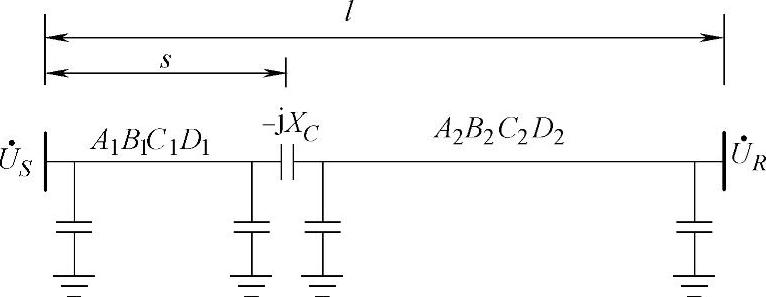
图4-4 带一个串联电容器组的输电线路

使用串联电容器降低串联感抗的效益定量称为串联补偿的“有效性”，计算串联补偿有效性的方法是基于输电线分布参数理论，适用于任何一种电容器布置方式的线路，而且还适用于研究带并联补偿的系统。(https://www.xing528.com)

本节以单电容器组接入线路中央为例分析串联补偿的“有效性”，其接线如图4-4所示，线路被电容器组分为两段，每段用它的ABCD参数表示，线路分析模型采用两个等效π形线路和将两段线路分开的电容器组成。

使用ABCD参数表示的串联补偿输电系统回路方程为

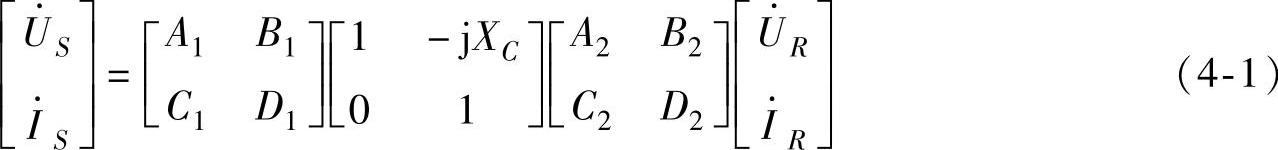
令系数矩阵为

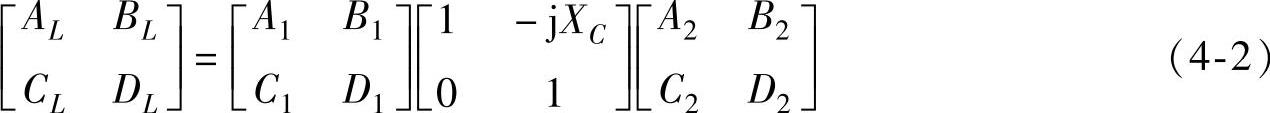
对式（4-2）进行矩阵的乘法运算，可以得到串联补偿输电系统的ABCD参数值：

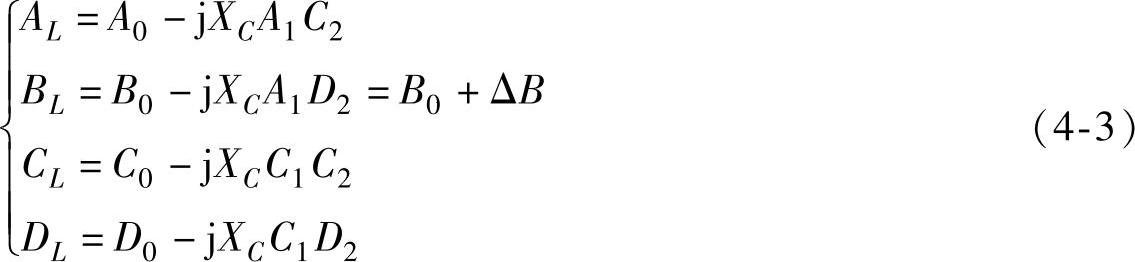
式（4-3）中，下标0表示不带串联补偿的整条线路的ABCD参数，补偿的“有效性”定义为传输电抗的净降低与串联补偿容抗之比。无补偿系统的传输电抗为B₀的虚部，该电抗通过B_L表达式的第二项得到降低，因此补偿的有效性K_x为

K_x=Re（A₁D₂）=Re（cosh（γs）coshγ（l-s）） （4-4）

式中，γ为输电线路的传输常数；s为从输电线路始端到串联电容器组的距离；l为线路长度。

从最有效使用串联容抗的角度看，当s=1/2l时，补偿的有效性K_x趋于最大。单个电容器组的最佳位置为输电线路中央，但是对于长输电线路来讲，其最经济的接入位置需要综合研究多种因素，充分考虑到设备的安装便利、运行维护费用和继电保护设定等。