特征根分析法的应用与优势

3.5.3.1 特征根分析法基本原理

特征根分析法又称模态分析法，其基本模型、概念和方法见3.2节内容，是通过建立系统的小扰动线性化模型，求解特征根、特征向量等来分析系统的动态响应的方法。

特征根分析法是控制理论中最基础的分析方法，构成了动态系统分析的理论基础，是校验其他分析方法正确性的基本工具，其优点是理论严密，物理概念清晰，分析准确度高，可得到大量有用信息，容易进行控制对策研究，通过比较控制对策施加前后特征根的变化确定其效果，而且有多种通用的特征根分析软件工具，便于分析工作的开展。

特征根分析法是小扰动分析方法，可以用于分析除暂态转矩放大作用之外的各种SSO问题，对于简单系统非常有效，在次同步振荡研究中已经得到了广泛应用，一般在工程上可将多机系统化简后用特征根法进行分析。

但是，特征根分析法用于次同步振荡分析也存在明显的缺点。首先是，存在严重的“维数灾”问题，因为次同步振荡涉及发电机轴系，而n质量块轴系模型的动态方程为2n维，使其“维数灾”问题有时比低频振荡分析中还严重，并且随着现代电力系统的规模越来越大，该问题愈加突出，因此特征根分析法一般只能计算小系统。还有，特征根分析法只能得到若干孤立点（特征根相应频率处）的动态特性，不能进行连续频率的特性分析，而且特征根与元件参数、运行参数的关系难以进行显式表达，因此振荡机理的物理透明度低，不利于机理分析和控制策略研究。另外，特征根计算要求有准确的系统和轴系参数，这大大限制了其应用。

3.5.3.2 特征根分析法算例

本节以IEEE第一标准模型（IEEE First Benchmark Model）为例，用特征根法分析其次同步振荡特性。IEEE第一标准模型由IEEE次同步谐振工作组于1977年提出，其系统结构如图3-16所示，各绕组参数、转子轴系模型参数、自然振荡频率等参数见附录A。

图3-16 IEEE第一标准模型

1.电网模型及参数

设u_d、u_q分别为发电机端电压的d轴和q轴分量，u_Cd、u_Cq分别为串联电容器两端电压的d轴和q轴分量，u_0d、u_0q分别为无穷大母线的d轴和q轴分量，i_d、i_q分别为线路电流的d轴和q轴分量。记R=R_T+R_L，X=X_T+X_L+X_S，系统在dq坐标系下的线性化方程为

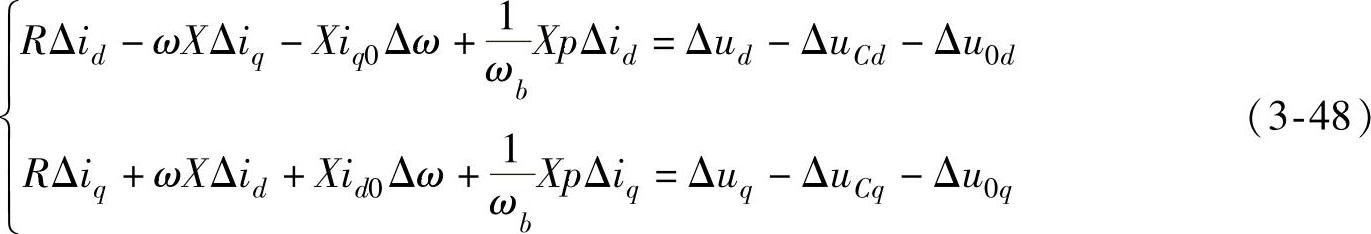
式中，，时间t的单位取s，其他变量均采用标幺值表示。设δ是以无穷大母线电压相量为参考时发电机转子q轴的角度，则u_0d与u_0q的表达式为

对其进行线性化处理后，可得

在dq坐标系下，串联电容器的电压与电流的关系式经线性化处理后，可得

2.同步发电机模型及参数

同步发电机的磁链和电压方程如式（2-3）、式（2-4）、式（2-5）和式（2-6）所示，同步发电机参数如表3-3所示，各符号含义参见第2章。

表3-3 同步发电机参数（pu）

3.转子轴系模型及参数

转子轴系模型如图2-15所示，将式（2-43）所示的轴系运动方程在初始运行点上线性化后，得到以下方程：

式中各符号含义同式（2-43）。质量块5对应于发电机转子轴段，故有Δδ₅=Δδ_G，Δω₅=Δω，ΔT₅=-ΔT_e；质量块6对应于励磁机转子，假定ΔT₆=0；并且K₀，1=K_6，7=0，D_0，1=D_6，7=0。

4.汽轮机和调速器模型及参数

汽轮机的传递函数框图如图2-10所示，其线性化方程为(www.xing528.com)

调速器模型采用图2-11所示的汽轮机机械液压调速系统，进行小扰动分析时，可忽略限幅环节，再将图2-12所示的传递函数框图进行等效变换后，得到其线性化方程为式（3-56）。

汽轮机和调速器的参数如表3-4所示。

表3-4 汽轮机和调速器模型参数（pu）

5.励磁系统模型及参数

励磁系统模型采用如图2-6所示的IEEE ST1A励磁系统模型，其参数见表2-1。在表2-1中，由于T_C=T_B，T_C1=T_B1，T_A=0，K_F=0，所以串联的领先-滞后校正环节不起作用，并联的励磁电压软反馈不起作用，对模型进行整理可得到以下方程：

ΔE_FD=-K_AΔV_t-K_LRΔI_FD （3-57）

式中，

6.全系统的状态方程

将式（3-48）～式（3-59）进行坐标变换及推导，消去中间变量，整理后可得到一组由25个一阶线性微分方程组成的方程组，它描述了图3-16所示电力系统的全部动态行为。系统的状态方程可合并写为

记为

式中，。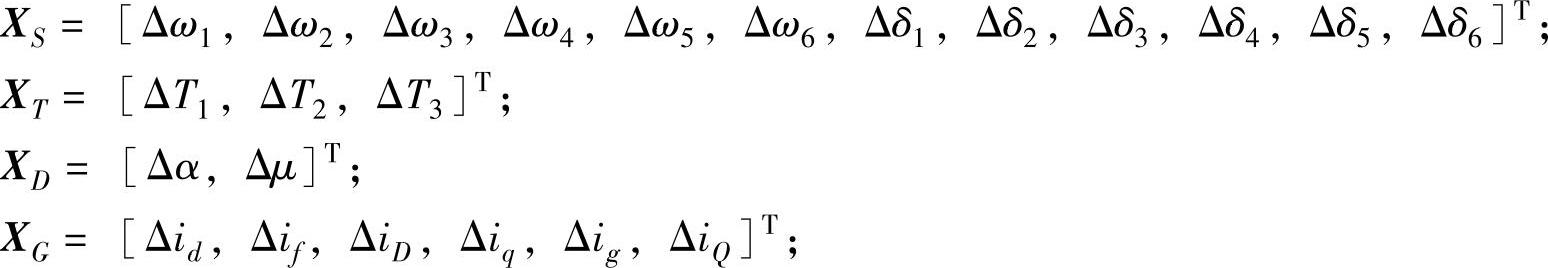

7.阻尼守恒与转移现象

定义串联补偿度k_c为

k_c=X_C/X_L （3-62）

式中，X_C为工频下串联电容器C的容抗；X_L为工频下的线路电抗。串联补偿度是影响SSO电气模态阻尼的主导因素，表3-5为k_c取0.1、0.3、0.5时，系统的特征根。

表3-5 不同串联补偿度情况下的特征根

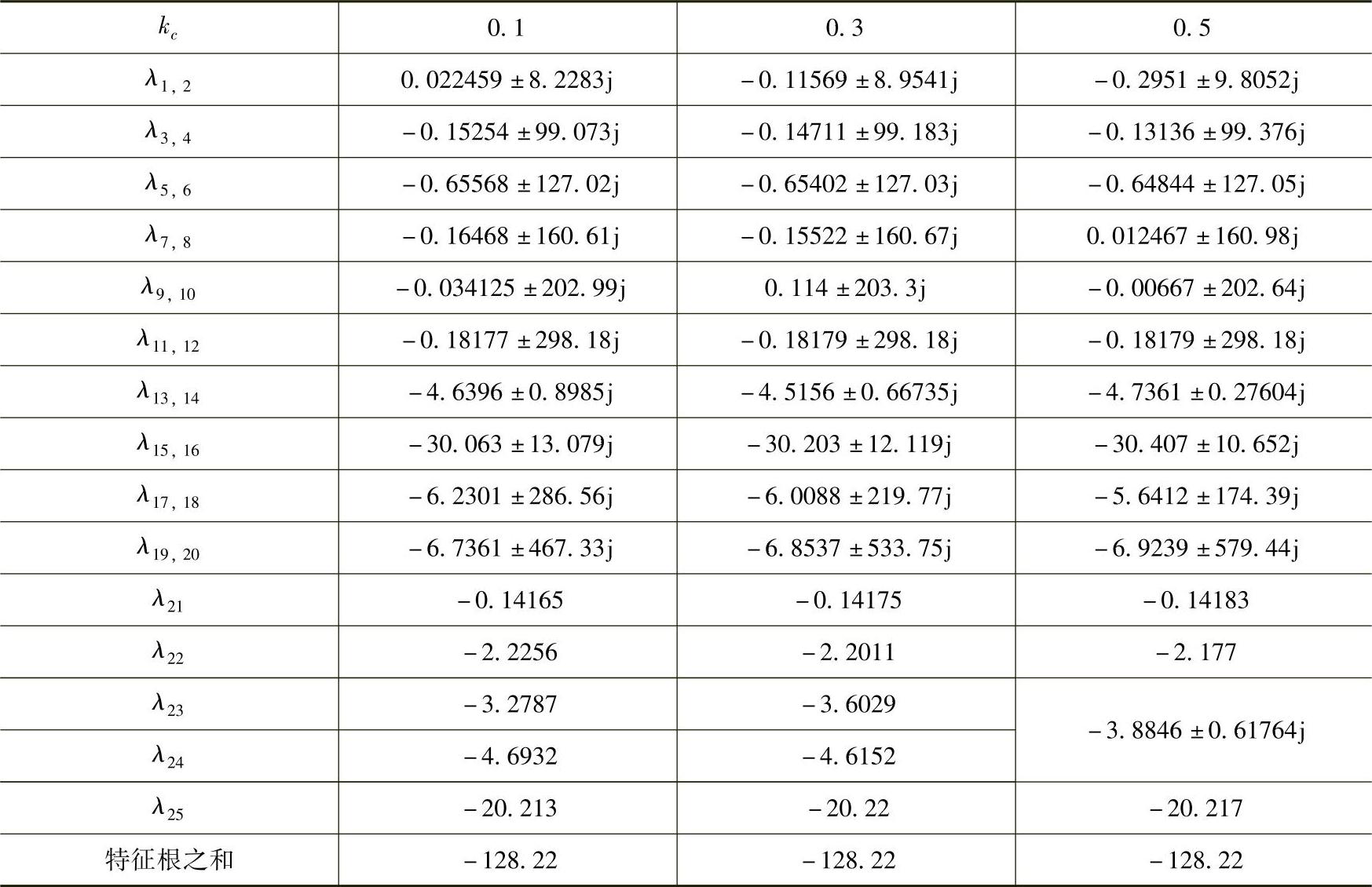
在表3-5中，λ_1，2代表将整个转子看作刚体时的振荡模态，属于低频振荡模态；λ_3，4～λ_11，12分别代表轴系的次同步振荡模态1～模态5，对应的扭振频率分别是15.7Hz，20.2Hz，25.6Hz，32.3Hz，47.4Hz。

根据矩阵的基本性质，矩阵的迹，即其对角线之和等于其所有特征根之和，对于实矩阵就是其所有特征根的实部之和。由于特征根的实部体现了系统的阻尼，所以矩阵迹可以看作系统的总阻尼^[16]。由表3-5可以发现，当串联补偿度k_c改变时，系统所有特征根之和保持不变，也就是说，k_c改变时系统总阻尼是守恒的。这一现象可通过分析式（3-51）、式（3-52）所示的串联电容器的状态方程来解释：因为参数X_C只在这两个状态方程中出现，并且不出现在状态矩阵的对角线上，说明系统总阻尼与其无关，所以当串联补偿度k_c改变时，系统总阻尼是守恒的。

由表3-5还可以看到，当k_c变大时，电气阻尼会从低频振荡模式转移到次同步振荡模式上。当k_c=0.1时，输电线路的总电抗较大，因此λ_1，2的实部为正，对应的阻尼为负，系统中如果没有加装PSS就可能发生低频振荡。当k_c增大为0.3、0.5时，相当于缩短了输电线路，增强了发电机与系统间的联系，因此λ_1，2的实部均为负，系统不会发生低频振荡。而当k_c=0.3时，λ_9，10的实部为正，对应振荡频率为32.37Hz；k_c=0.5时，λ_7，8的实部为正，对应振荡频率为25.63Hz。这是因为随着k_c的增大，电气系统的自然振荡频率f_e也增大，其次同步互补频率f_er=f₀-f_e相应减小，负阻尼转移到轴系频率较低的模态。