轴系扭转与相互作用的影响分析

当发电机转子上产生频率为轴系自然扭振频率的振荡时，还有可能因为机械部分与电气部分的相互作用产生不稳定振荡，这就是轴系扭转相互作用。下面对于图3-1所示的带串联电容器的简单输电系统，分析其轴系扭转相互作用的产生机理^[11]，这里各变量均取标幺值，其中角速度基值为ω₀，时间基值为1/ω₀。

为简化分析，设在t=0时刻，d轴和a相绕组轴系重合，以其为角度零点。假设系统在运行平衡点受到幅值很小的扰动，使得发电机转子产生了频率标幺值为λ、幅值为A的角位移增量，即发电机转子的角位移为

θ=θ₀+Δθ=t+Acosλt （3-21）

角位移的增量为

Δθ=Acosλt （3-22）

对应上述角位移，发电机转子的角速度为

ω=pθ=ω₀+Δω=1-λAsinλt （3-23）

角速度的增量为

Δω=-λAsinλt （3-24）

对于同步发电机，其电压方程为

由上述方程可见，发电机端电压的变化与定子电流、角速度、磁链有关。为简化分析，不妨将定子绕组电阻合并到外电路阻抗中，同时忽略发电机变压器电动势，即不考虑磁链变化的影响，这时有

在稳态运行时，发电机以恒定转速1旋转，有

由式（3-26）、式（3-27）可得电压增量的方程为

根据派克反变换有

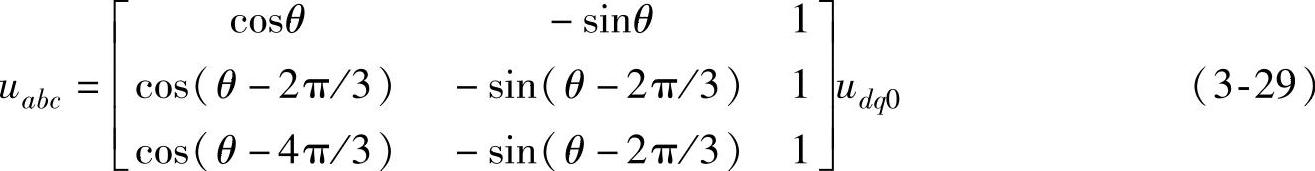
这里忽略三相不对称的影响，即零序分量为0。下面以a相为代表进行分析，其电压为

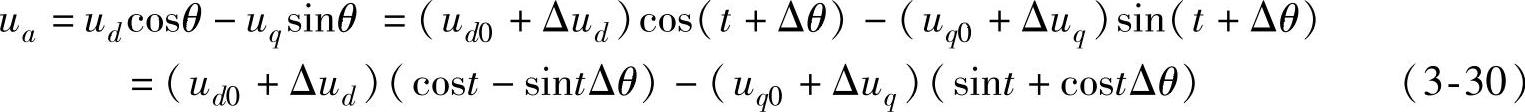
忽略二次项可得到其增量方程为

Δu_a=costΔu_d-u_d0sintΔθ-sintΔu_q-u_q0costΔθ （3-31）

将式（3-27）、式（3-28）代入，同时不考虑磁链变化的影响，可得

Δu_a=（ψ_q0sint-ψ_d0cost）Δθ-（ψ_q0cost+ψ_d0sint）Δω （3-32）

将式（3-22）、式（3-24）代入可得

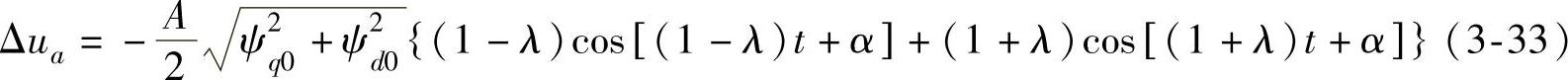
式中，

α=arctan（ψ_q0/ψ_d0） （3-34）

在式（3-33）中，将α分别用α-2π/3和α-4π/3代替，就可以得到其他两相的电压增量。该式表明，发电机转子上频率为λ的振荡分量，将在定子上产生次同步频率1-λ和超同步频率1+λ的两个电压分量。(www.xing528.com)

下面进一步分析次同步分量和超同步分量产生的电磁转矩。

1.次同步分量产生的电磁转矩

对于次同步电压分量，如果串联电容器与定子回路中的电抗刚好在次同步互补频率1-λ下形成谐振，则线路电抗为零，此时线路总阻抗等于定子回路中的总电阻R，产生的次同步电流为

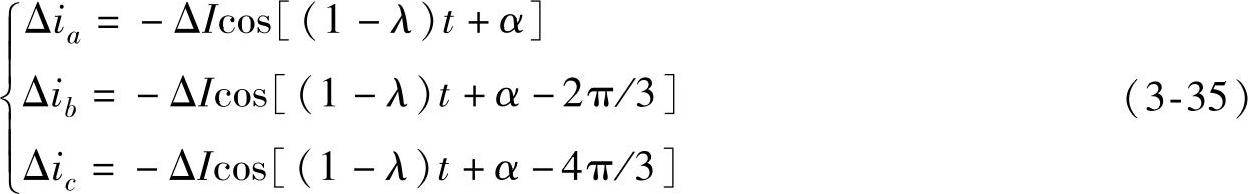
式中，

考虑上述三相对称次同步电流增量的作用，由派克变换可得它们在发电机转子上产生的d轴、q轴电流增量为

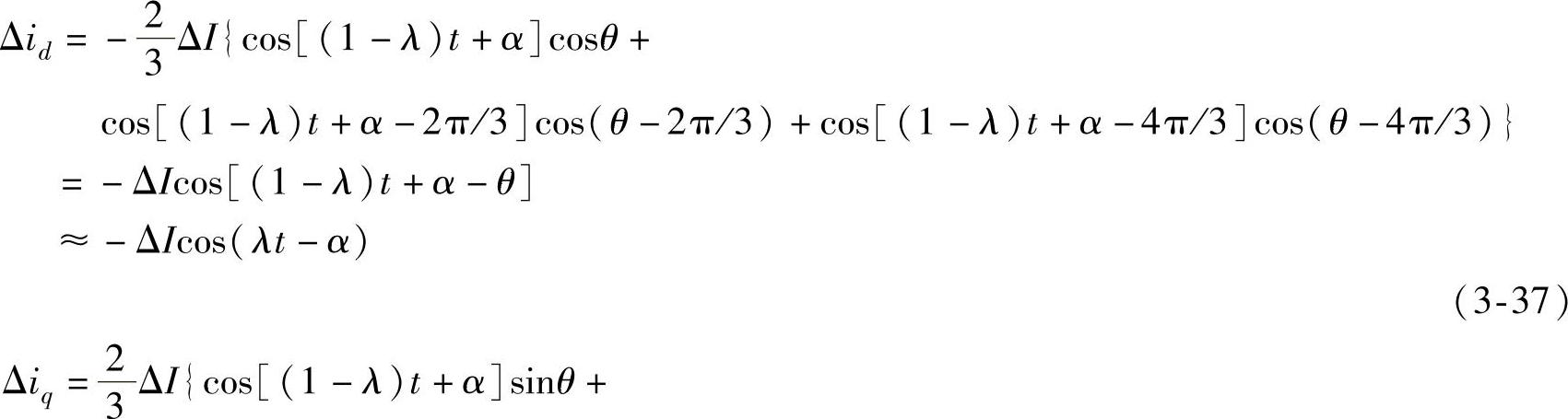
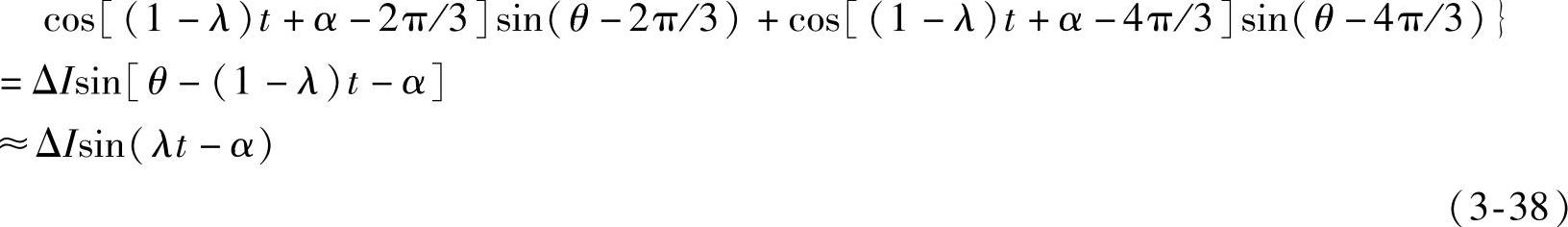
由式（3-36）、式（3-37）、式（3-38）可以求出该次同步电流增量在发电机转子上产生的电磁转矩增量为

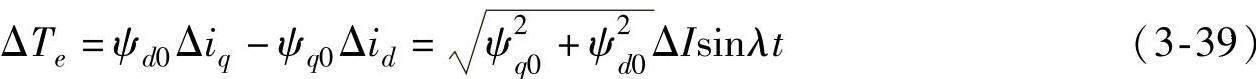
将式（3-24）、式（3-36）代入可得

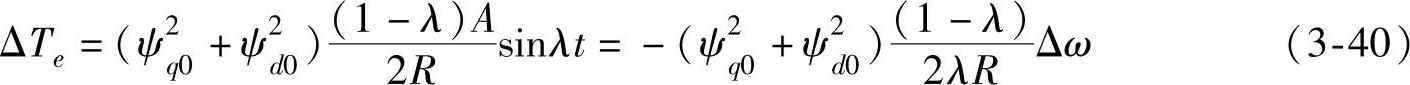
式（3-40）表明，当发电机转子振荡频率与定子回路的LC谐振频率互补时，将产生很大的次同步电流，并且在转子上产生与Δω反相的电磁转矩，它对该转子振荡分量产生负阻尼作用。

2、超同步分量产生的电磁转矩

在工频下，因为输电线串联补偿度一般小于1，所以串联电容器容抗小于输电线感抗。对于超同步电压分量，串联电容器的容抗变小，输电线的感抗变大，使得定子回路总电抗X′变大。同时因为输电线电阻一般远远小于感抗，有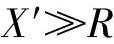，所以定子回路的超同步阻抗主要为感抗，产生的超同步电流近似为

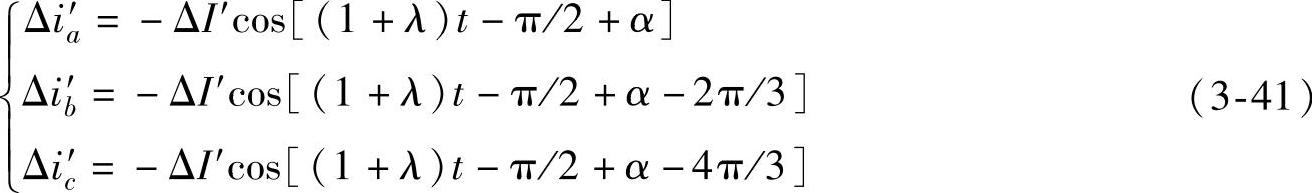
式中，

对比式（3-42）与式（3-36）可知，超同步电流远远小于次同步电流。考虑上述三相对称超同步电流增量的作用，由派克变换可得它们在发电机转子上产生的d轴、q轴电流增量为

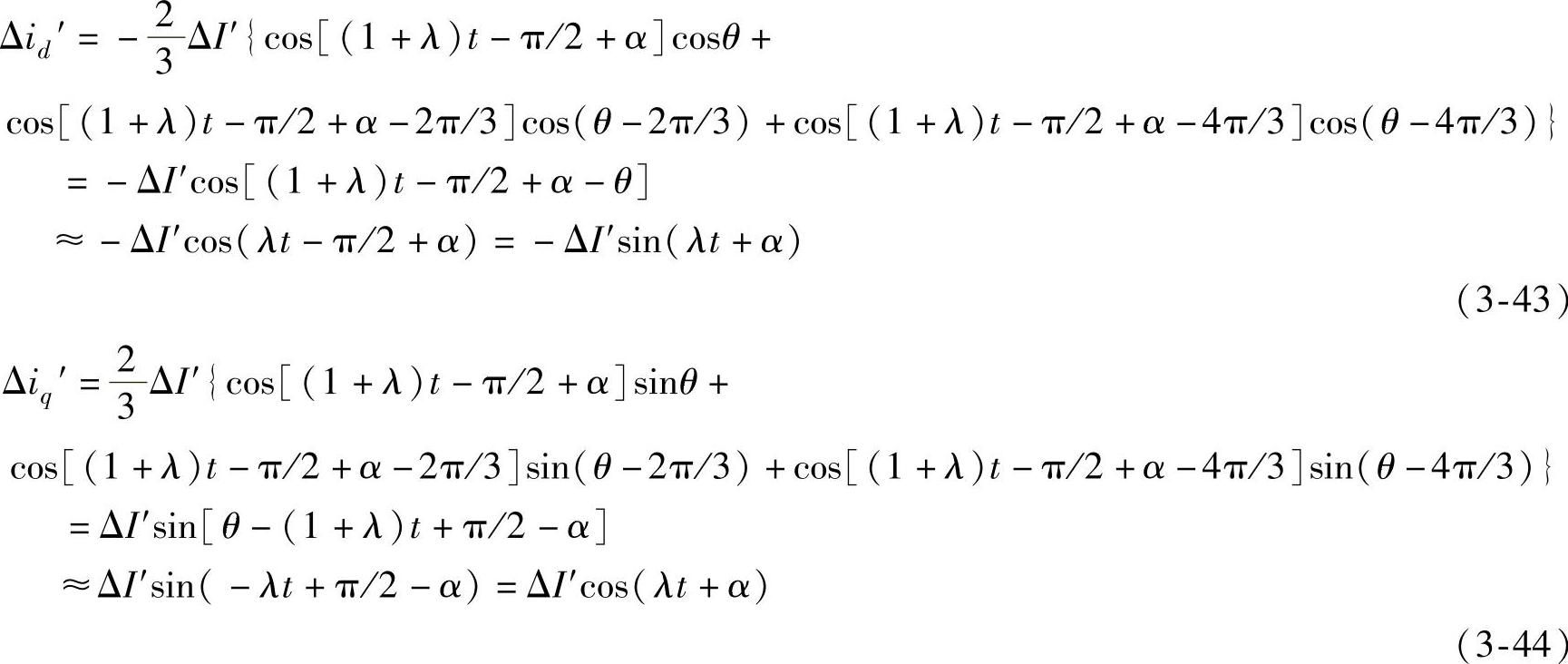
由式（3-42）、式（3-43）、式（3-44）可以求出该超同步电流增量在发电机转子上产生的电磁转矩增量为

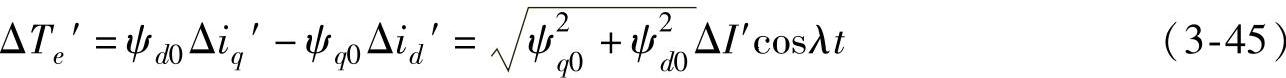
将式（3-22）、式（3-42）代入可得：

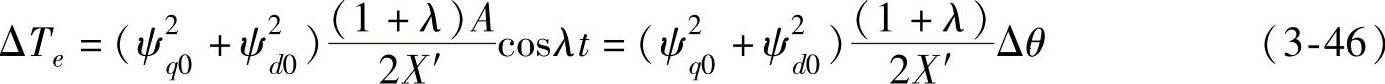
式（3-46）表明，发电机转子振荡产生的超同步电流在转子上产生的电磁转矩与Δθ同相，它对该转子振荡分量产生正的同步作用。

综合上面的分析，发电机转子振荡将在定子回路产生次同步电流和超同步电流两个电流分量。当转子振荡频率与定子回路谐振频率刚好互补时，定子回路次同步阻抗主要为电阻R，使得次同步电流的幅值大大增加，产生的电磁转矩为负阻尼转矩。而定子回路超同步电抗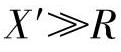，使得超同步电流很小，产生的电磁转矩也很小，主要为正的同步转矩，因为这一转矩一般远远小于轴系弹性作用产生的同步转矩，因此可以忽略它对转子动态过程的影响。实际上，式（3-25）中被忽略的转子磁链变化量也会和定子稳态磁链产生其他电磁转矩分量，但是都远远小于式（3-40）所示的电磁转矩。

总体来说，当在转子轴系自然振荡频率下，如果式（3-40）所示负阻尼大于机械阻尼和其他电气阻尼之和时，发电机转子轴系与电气系统之间将出现增幅或者持续的谐振，这就是轴系扭转相互作用。