建立Yd联结变压器的电磁暂态数学模型

变压器的励磁电抗非常大，通常将其忽略^[11]。假设变压器接线为Y₀/Y₀，其两侧中性点接地，且三相参数对称，双绕组变压器的一相等效电路如图2-18所示。图中，变压器电压比为1∶n，R_T、L_T（工频下，L_T（pu）=X_T（pu）不予区分）为各相绕组的电阻和漏抗标幺值。

图2-18 双绕组变压器等效电路

1.abc坐标系中的变压器方程

对于图2-18所示的电路，设i_i，abc，=[i_ia，i_ib，i_ic]^T，i′_i，abc=[i′_ia，i′_ib，i′_ic]^T，i_j，abc=[i_ja，i_jb，i_jc]^T，u_i，abc=[u_ia，u_ib，u_ic]^T，u′_i，abc=[u′_ia，u′_ib，u′_ic]^T，u_j，abc=[u_ja，u_jb，u_jc]^T，，可以列出以下方程：

由于-i_j，abc=i′_i，abc，代入式（2-59）可得：

联立式（2-61）和式（2-63）可得：

令Y_T=Z^-1_T，则式（2-64）可变为

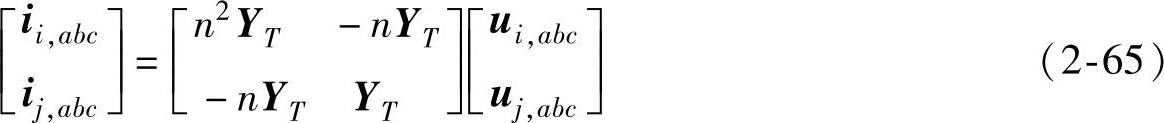
在潮流和稳定研究中，广泛采用图2-18所示的等效电路来表示双绕组变压器。在分析次同步振荡问题时，可以将变压器阻抗与线路阻抗合并考虑。

三绕组变压器、自耦变压器、移相变压器的数学模型可参考文献[4，11，16]。

2.dq0坐标系中的变压器方程

将式（2-60）两边同乘以派克变换矩阵P，可得

(www.xing528.com)

由矩阵求导性质，即ApB=p（AB）-（pA）B，以及可得

式中，。

同理，将式（2-62）两边同乘以派克变换矩阵P，可得

（Z_T+ωL_TA）i_j，dq0=-（nu_i，dq0-u_j，dq0） （2-68）

将式（2-67）代入式（2-66）并与式（2-68）联立，可得

3.变压器接线方式对模型的影响

对于Yy、YNyn、Yyn或Dd联结的变压器，一般均采用12点接线，变压器两侧电量相位分别相同，但对于Yd联结的变压器，变压器两侧电量相位不相同，应予以注意。下面以Yd11联结变压器为例，通过图2-19说明变压器两侧电量的相位关系。

在建立Yd联结变压器的电磁暂态数学模型时，要注意根据变压器接线不同，将两侧的坐标转适当角度，在此前提下，在不同的坐标系上观察空间向量，即得到所需的坐标转换量。以Yd11接线变压器为例，可以取Y侧轴线领先Δ侧轴线30^o，如图2-20所示。

图2-19 Yd11联结变压器及其电量关系

图2-20 Y，d11接线变压器两侧坐标

图2-21 并联电容器接线图