在进行同步发电机的暂态分析时,可以根据同步发电机的方程式画出相应的等效电路,这样比较直观也便于记忆,然后由此定义运算电抗和实用参数。
2.2.5.1 q轴等效电路、运算电抗及实用参数
q轴磁链方程为
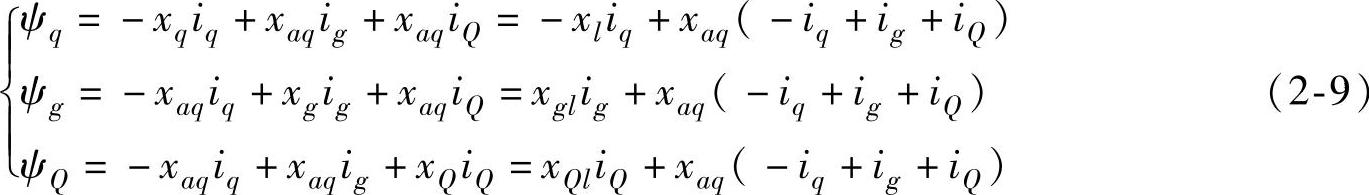
式中,xl、xgl和xQl分别为q绕组、g绕组和Q绕组的漏抗。由式(2-9)可得图2-3a中的q轴电抗、电流和磁链关系图。再由q轴电压方程:
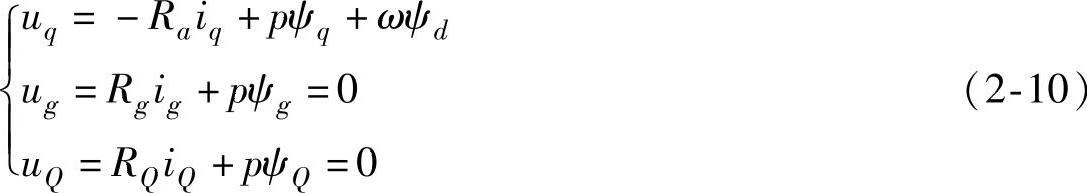
最终可得图2-3b中的q轴等效电路。
当各电流初值均为零时,采用拉氏变换后,方程的形式不变,但p变成一个复变量。根据q轴等效电路,通常定义q轴运算电抗为
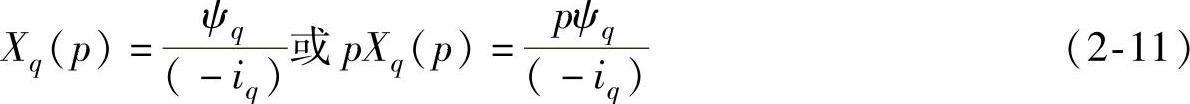
则根据图2-3b(由o′-q′向电机内部看,“∥”表示并联)可得
pXq(p)=pxl+(pxaq)∥(pxgl+Rg)∥(pxQl+RQ) (2-12)
从而

一些文献根据式(2-13)把Xq(p)表示成图2-3c的形式,即视 为“电容”,而视xl、xaq、xgl、xQl为“电阻”,从而直接写出表达式。在电机过渡过程的解析分析及频域分析中常采用运算电抗的概念。
为“电容”,而视xl、xaq、xgl、xQl为“电阻”,从而直接写出表达式。在电机过渡过程的解析分析及频域分析中常采用运算电抗的概念。

图2-3 q轴等效电路及运算电抗
同步发电机稳态过程、次暂态过程以及暂态过程的等效电抗也可以从运算电抗给出定义,下面给出q轴实用参数的定义。
1)稳态情况下,t→∞,p=0,q轴同步电抗为
Xq(p)=Xq(0)=xq=xaq+xl (2-14)
2)在起始次暂态过程中,t=0,p→∞,q轴次暂态电抗为
x″q=Xq(∞)=xl+xaq//xgl//xQl (2-15)
3)在暂态过程中,t=0,p→∞,q轴阻尼绕组Q的电流几乎衰减到零,因此不考虑该阻尼绕组,q轴暂态电抗为
x′q=Xq(∞)=xl+xaq//xgl (2-16)
4)q轴开路次暂态时间常数T″q0的定义为p→∞,定子等效绕组开路,从阻尼绕组Q端口看过去的等效时间常数。

5)q轴开路暂态时间常数T′q0的定义为p→∞,定子等效绕组和阻尼绕组Q开路(在暂态过程中,阻尼绕组Q的电流几乎衰减到零,可认为阻尼绕组Q开路),从阻尼绕组g端口看过去的等效时间常数。

6)q轴短路次暂态时间常数T″q的定义为p→∞,定子等效绕组短路,从阻尼绕组Q端口看过去的等效时间常数。

7)q轴短路暂态时间常数T′q的定义为p→∞,定子等效绕组短路,阻尼绕组Q开路(在暂态过程中,阻尼绕组Q的电流几乎衰减到零,可认为阻尼绕组Q开路),从阻尼绕组g端口看过去的等效时间常数。

2.2.5.2 d轴等效电路、运算电抗及实用参数(https://www.xing528.com)
与q轴相似,由d轴磁链方程:

可导出图2-4a所示的d轴电抗、电流和磁链关系图。再由d轴电压方程:

可导出图2-4b中的d轴等效电路。
与q轴相似,定义d轴运算电抗:

则由图2-4b有
pXd(p)=pxl+(pxad)//(pxfl+Rf)//(pxDl+RD) (2-24)
从而

式(2-25)的Xd(p)可用图2-4c中的等效电路直接表示。
下面给出d轴实用参数的定义。
1)稳态情况下,t→∞,p=0,d轴同步电抗为
Xd(p)=Xd(0)=xd=xad+xl (2-26)
2)在起始次暂态过程中,t=0,p→∞,d轴次暂态电抗为
x″d=Xd(∞)=xl+xad//xfl//xDl (2-27)
3)在暂态过程中,t=0,p→∞,d轴阻尼绕组D的电流几乎衰减到零,因此不考虑该阻尼绕组,d轴暂态电抗为
x′d=Xd(∞)=xl+xad//xfl (2-28)
4)d轴开路次暂态时间常数T″d0的定义为p→∞,定子等效绕组开路,从阻尼绕组D端口看过去的等效时间常数。
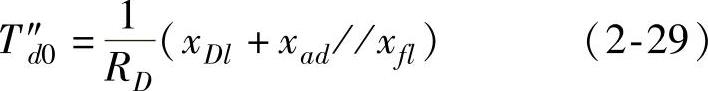
5)d轴开路暂态时间常数T′d0的定义为p→∞,定子等效绕组和阻尼绕组D开路(在暂态过程中,阻尼绕组D的电流几乎衰减到零,可认为阻尼绕组D开路),从励磁绕组f端口看过去的等效时间常数。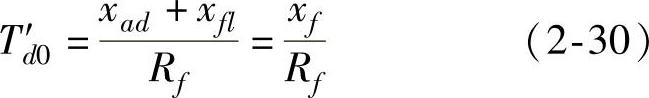

图2-4 d轴等效电路及运算电抗
式中,令xf=xad+xfl。
6)d轴短路次暂态时间常数T″d的定义为p→∞,定子等效绕组短路,从阻尼绕组D端口看过去的等效时间常数。

7)d轴短路暂态时间常数T′d的定义为p→∞,定子等效绕组短路,阻尼绕组D开路(在暂态过程中,阻尼绕组D的电流几乎衰减到零,可认为阻尼绕组D开路),从励磁绕组f端口看过去的等效时间常数。

应该强调的是,上述时间常数的单位为(pu)。若要化为以s为单位,则要乘以tB,即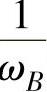 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




