转子平衡力学条件详解

机器中绕轴线旋转的零部件称为机器的转子。如果一个转子的质量分布均匀，制造和安装都合格，则运转是平稳的。理想情况下，其对轴承的压力，除重力之外别无其他的力，即与转子不旋转时一样，只有静压力。这种旋转与不旋转时对轴承都只有静压力的转子称为平衡的转子。如果转子在旋转时对轴承除有静压力外还附加有动压力，则称之为不平衡的转子。转子如果是不平衡的，附加动压力将通过轴承传达到机器上，引起整个机器的振动，产生噪声，加速轴承的磨损，降低机器的寿命，甚至使机器控制失灵，发生严重事故。

任何一个转子匀速转动时，体内无数个质点都将产生惯性力，组成一个惯性力系；要确定这个转子是否为平衡转子，必须根据其惯性力系合成的结果而定。这个合成结果，可以利用理论力学中的力系向任一点简化的原理来分析。

首先，假定转子是绝对刚性转子，即刚体，而理想的刚体在任何力作用下都不会产生变形。这个假设当然与事实不符，事实上任何物体在力的作用下都会变形，只是程度不同。但如果一般机器的转子重量不大，转速不高，转轴跨距不长，旋转时转子变形很小，其影响可略去不计，则可假设这种转子是刚性的。

图 9-1

设有一个不平衡的刚性转子，如图9-1所示，其质量为M，以等角速度ω绕一固定轴旋转，取转轴上任一点O为坐标原点，转轴为z轴，并做出相应的Ox及Oy轴。转子质心的坐标为C（x_c，y_c，z_c），沿坐标轴方向单位矢量为i、j、k。设质心C对旋转轴z的矢径为r_c，则

r_c=x_ci+y_cj

同样，设转子中任一质点m_i的坐标为m_i（x_i，y_i，z_i）对转轴的矢径为r_i，则

r_i=x_ii+y_ij

当转子以等角速度ω旋转时，质点m_i产生的离心力为F_i=m_ir_iω²，其指向为离心方向，即为矢径r_i的方向，故可写成：

F_i=m_ir_iω²=m_iω²（x_ii+y_ij） （9-1）

它在坐标轴上投影为

式中，i=1，2，3，…，n。

诸F_i构成一个惯性力系。由力学原理可知，将这个惯性力系向坐标原点O简化（O点称为简化中心），一般可得到一个力R_o（称为力系的主矢）和一个力偶M_o（称为力系向O点简化的主矩），这个主矢作用于O点并等于力系中所有各力的矢量和，而主矩等于力系所有各力对O点的矩矢的矢量和，即

(www.xing528.com)

将公式（9-1）代入公式（9-3）得

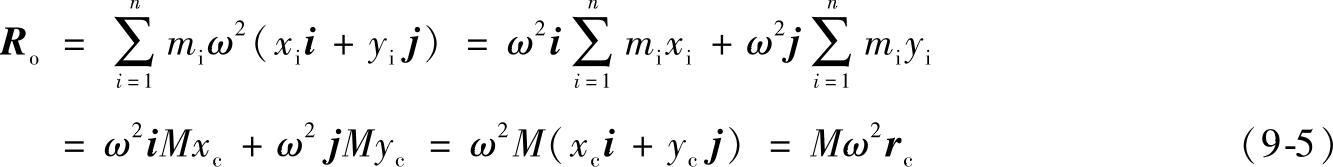
由此可见，简化的主矢R_o的大小与方向和转子质心的离心惯性力相等，只不过作用于O点即R_o∥r_c，其大小与方向和简化中心O点的位置无关。

惯性力系向O点简化的主矩可写为

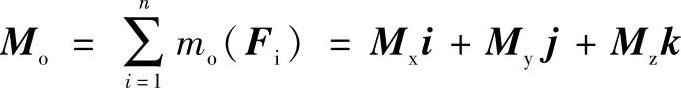
式中，M_x、M_y及M_z为主矩M_o在坐标轴上的投影，其大小等于力系所有各力对该轴之矩的代数和，显然，它们都和O点的位置有关。

M_z=∑m_z（F_i）=0（因为F_i通过z轴）

式中，J_yz=∑m_iy_iz_i和J_zx=∑m_iz_ix_i均称为转子的惯性积或转子的离心转动惯量。于是

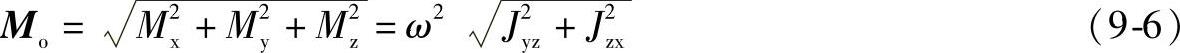
因此，转子的惯性力向任一点简化的结果一般得到一个力（即主矢：R_o=Mr_cω²，作用于O点，方向和r_c平行）和一个力偶（即主矩：）。

转子在旋转时，主矢和主矩的方向都在变化，其矢量随同转子一同旋转成为引起轴承振动的激发源。所以，转子平衡的必要与充分条件是惯性力系向任一点简化的主矢和主矩都为零，即

由R_o=0，则r_c=0，这说明旋转轴必定通过质心C；由M_o=0，则J_yz=J_zx=0，满足此条件的转轴z在力学中称为惯性主轴，通过质心的惯性主轴称为中心惯性主轴。因此，欲消除转子对轴承的动压力必须也只需旋转轴是中心惯性主轴。虽然任何形状的转子通过其质心都存在着三个互相垂直的中心惯性主轴，但不一定和旋转轴重合，除非转子对旋转轴为中心的质量分布对称。所以，一般转子几乎都是不平衡的。要使一个不平衡转子变为平衡转子，就要重新调整转子质量的分布，即在某个局部加重或去重，使转子的中心惯性主轴和旋转轴一致，这时，其惯性力系能够满足公式（9-7），转子成为平衡的转子。