如何正确选择通风机设计参数？

为便于说明问题，我们将【例5-13】中计算的4—73型和9—35型通风机的性能（按标准进气状态）通过设计点A（q_V=24m³/s，p_tF=4413Pa）绘制出两通风机的有因次性能曲线，如图5_-9所示。

通过【例5-13】的计算和图5-9所示，我们可以知道，当利用现有的空气动力学略图和无因次性能曲线进行通风机相似设计时，在不限制通风机转速n和当量直径D的条件下，我们能够选择任一类型的通风机（如4—73型和9—35型），来满足任一流量（如q_V=24m³/s）和全压（如p_tF=4413Pa）的要求，而通风机都能够在它们自己的内效率最高点η_tF·in，max（如4—73型风机η_tF·inmax=0.93；9—35风机η_tF·inmax=0.68）下运行，通过设计点（见图5-9中的A点、q_V=24m³/s，p_tF=4413Pa），可以做出无数条通风机的性能曲线，而这些曲线就代表着各种不同类型通风机的性能。

但是，在我们利用现有空气动力学略图和无因次性能曲线进行通风机相似设计时，不能忽视的一点，就是我们所选择通风机的强度问题，因为通风机的叶轮在运转时，叶片产生应力的大小与当量速度的平方以及叶片宽度的平方成正比例关系，对于特定通风机来说，叶轮宽度为一定值，此时，必须限制其当量速度，才能保证通风机的安全运行。我们经常将叶轮在使用一般钢材（如Q235、Q345）的情况下，按强度要求计算出不同类型通风机的允许最大当量线速度u_max。这样，当按一般常规进行通风机的设计时，通常不会产生强度不够的问题。

说到这里，我们可以知道，虽然在空气性能上讲，根据已知的流量和全压能够选择任一类型的通风机来满足其要求，但由于强度方面的原因，我们必须对当量速度u根据不同类型通风机叶轮的结构情况加以限制，这就在很大程度上缩小了选择通风机类型的范围。在没有可靠资料的情况下，有时不得不选择内效率低，当量直径大但在结构和强度上可靠的通风机来进行设计。

因此，当我们在实际设计通风机时，在能满足需要的流量q_V和全压q_tF的情况下，要全面衡量各种类型通风机的特性，一方面要求产品的内效率高（这很容易在无因次性能曲线中看出），另一方面要求产品的体积小、重量轻（可比较各类型通风机的比直径D_s值），同时，又要求产品的强度高、运行可靠，这就需要减少通风机的当量速度u（也就是减小当量直径D和转速n），然而，为了保证需要的流量q_V和全压p_tF，产品又必须具有一定的当量直径D和转速n，这就需要根据我们掌握的各种不同类型通风机的空气动力学略图和无因次性能曲线中的各参数，加以分析、比较后，作出合理的选择。

为便于分析、比较，我们可将不同类型通风机，在内效率最高点时的各无因次性能参数和要比较的其他参数列于表5-8中作为例子，我们仅列出了4—73型、9—35型与8—19型的通风机的参数值，实际上，应该列出更多类型通风机的参数值，而且越多越好，因为它能帮助我们在更广泛的参数中，选择出适合于我们设计产品的数据。(www.xing528.com)

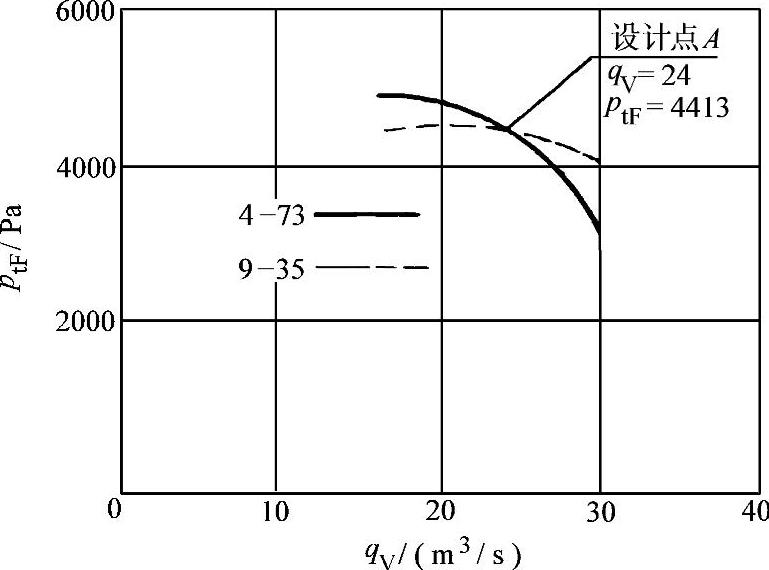
图5-9 4—73与9—35通风机性能曲线

表5-8 各类型通风机设计参数表

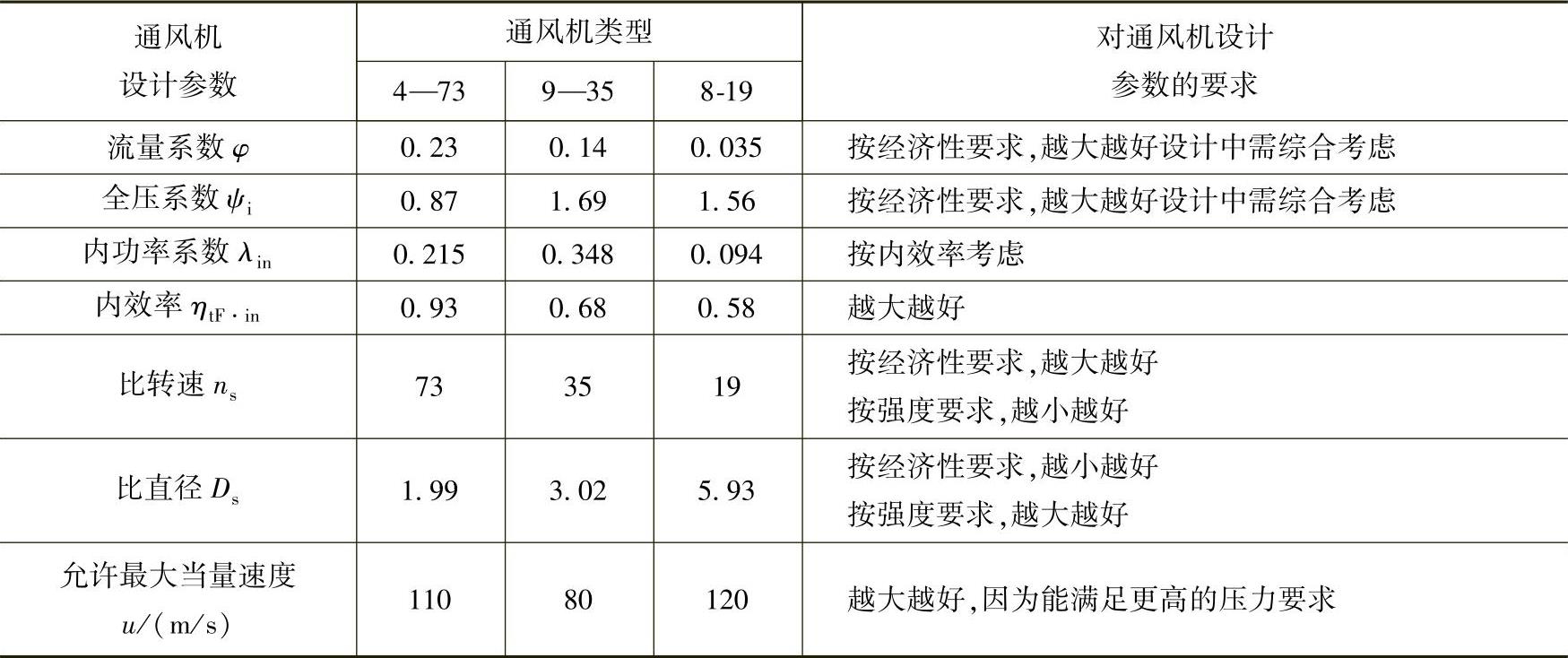
空气动力学略图中的各数值，以及几何形状，也是我们选择设计通风机的重要依据，不可忽视。比如，当设计排尘通风机时，就要选择叶片数量少的通风机，至于在众多不同类型通风机中，到底选择何种类型通风机为宜，那就要由设计者通过全面衡量后，作出最后决定。