空气动力学略图与无因次性能曲线

当我们设计出一台通风机后，就可以绘制出这台通风机的有因次的几何图形；经过性能试验，又可以绘制出在直角坐标上各种流量下的有因次性能曲线。图5-1是一台离心通风机产品或模型的几何尺寸图和在标准进气状态下转速n=1450r/min的性能曲线图。

根据离心通风机的几何尺寸图和性能曲线图（见图5-1），可以绘制出8—19型离心通风机的空气动力学略图和无因次（量纲为一）性能曲线，如图5-2所示。

为了设计上计算的方便，我们将空气动力学略图中叶轮外径（当量直径）D的尺寸定为100，则根据相似风机之间几何相似的理论，即可得出空气动力学略图中的其他所有尺寸。

比较图5-1a和图5-2a，其中所有对应部位尺寸的比值相等，比例常数为10；而且在两个图中，所有部位的尺寸与叶轮外径D尺寸的比值均对应相等。

由此可见，以通风机叶轮外径D=100，其他尺寸按叶轮外径的百分比数绘制的通风机图形，即为空气动力学略图。

图 5-1型离心通风机

a）几何尺寸图 b）性能曲线图

利用空气动力学略图，可以很快的求出我们所要设计通风机的几何尺寸；比如，图5-2a虽然是由得出的，但如果要设计的风机，只要用比例常数500/100=5乘以空气动力学略图中的数值即可。此时，产品与空气动力学略图中对应部位的角度不变，如叶片的进口角β₁和出口角β₂不变。

通风机的无因次性能曲线是利用基本无因次性能参数公式，将有因次性能参数换算成无因次性能参数，并绘制成曲线的。

图5-2 8—19型离心通风机

a）空气动力学略图 b）无因次性能曲线

现将图5-1b变换成图5-2b的过程，举例如下：

先将图5-1b中横坐标的流量分出几点，例如分为q_V=（0、1.043、1.31、2.086、2.98、4）m³/s六个点，并分别查出，在这些流量下纵坐标对应的各有关参数值，并列在表5-1中：

以下按该风机内效率最高点_ηtF·in=0.58（第4点）为例进行计算。

已知该风机参数：

D=1m(www.xing528.com)

n=1450r/min

ρ=1.2kg/m³

可求得

于是，可求得该风机无因次性能参数：

对应点的内效率和内静压效率相等，

η_tF·in=0.58，η_sF·in=0.50

用同样方法，可将表5-1中的其他各有因次性能参数，变换成无因次性能参数：见表5-2。

表 5-1有因次性能参数

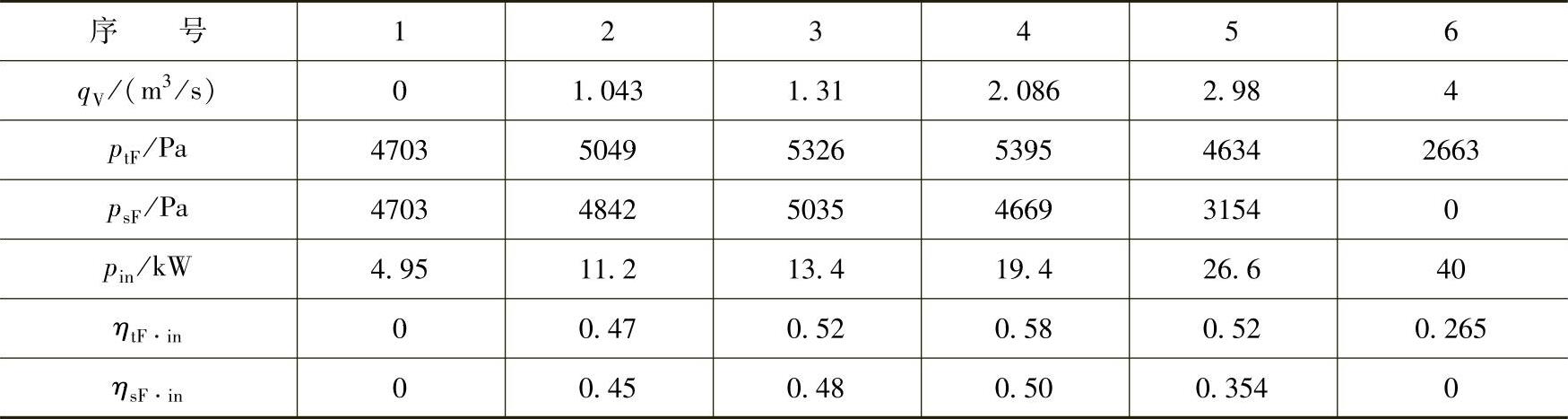
表5-2 8—19型无因次性能参数

将表5-2中所列数据点在直角坐标上并连接成圆滑的曲线，就成为图5-2b的8—19型离心通风机的无因次性能曲线了。

表5-1中的q_V=0（第一点）是通风机工作的特例之一，它表示管网阻力等于无限大时通风机的特性，此时q_V=0，p_tF=p_sF，η_tF·in=0，与此相对应的无因次性能参数，φ=0，ψ_t=ψ_s，η_tF·in=0，η_sF·in=0。

表5-1中的q_V=4（第六点）是通风机工作的特例之二，它表示管网阻力等于零时通风机的特性，此时，q_V=q_Vmax=4，p_tF=p_dF，p_sF=0，η_sF·in=0。于此相对应的无因次性能参数，φ=φ_max=0.067，ψ_t=ψ_d，ψ_sF=0，η_sF·in=0。

利用无因次性能曲线，可以很快的求出我们所要设计通风机的有因次性能曲线；因为前者本来就是由后者在特定的ρ、n、D情况下得出的，因此，只要作相反的运算即可。