如何识别现象相似的条件

在几何相似的两体系中，进行同一性质的过程，而且体系中各对应点上表示现象特性的同类量的比值等于常数，即成比例关系时，则此两体系称为互相相似的现象。对于两通风机的流动过程来说，必须具备下列条件，才能称为现象相似。

1.几何相似

相似的现象只能发生在几何相似的体系内，所以几何相似是先决条件。我们知道，对应边成比例，对应角相等的两三角形是相似三角形。那么，就离心通风机的实物和模型来说，所谓几何相似是指：

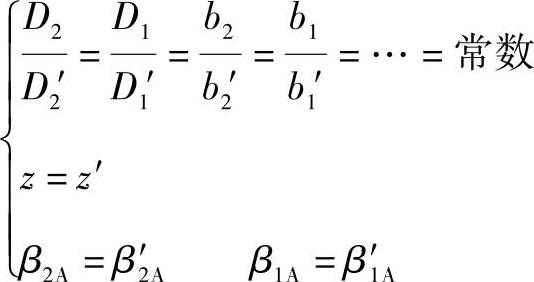
式中，带“′”者是对模型而言，不带“′”者是对实物而言。

严格地说，几何相似还应包括通风机的叶片厚度，叶轮和进风口间的间隙和表面粗糙度等。但这些尺寸相似与否对通风机性能的影响较小，故可忽略不计。

2.运动相似

实物和模型内各对应点的同类速度方向相同，大小的比值等于常数时，叫做运动相似。就通风机叶轮内的流动过程而言，运动相似是指：

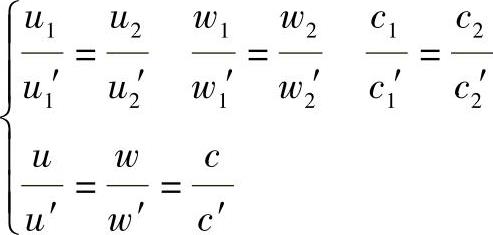
即对应点的速度三角形相似，且所有对应点两速度三角形大小相差的倍数相同。

3.动力相似

实物和模型内各对应点的同类力方向相同，而大小比值等于常数时，叫作动力相似。就通风机的流动而言，作用在基元流体上的主要力有惯性力I，粘性力R和总压力p_t，动力相似是指：

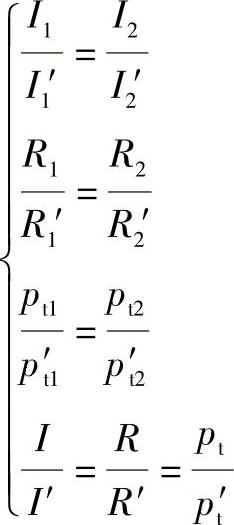
即对应点的力多边形相似，且所有对应点两力多边形的大小相差的倍数相同。根据理论力学：

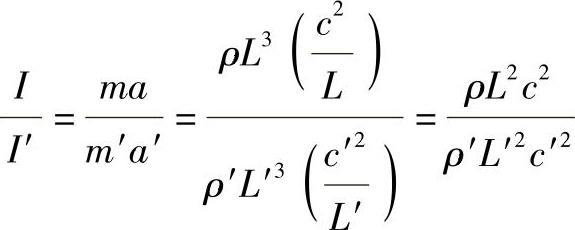
式中 ρ——气体的密度；

L——尺寸；

c——速度。

根据流体力学(www.xing528.com)

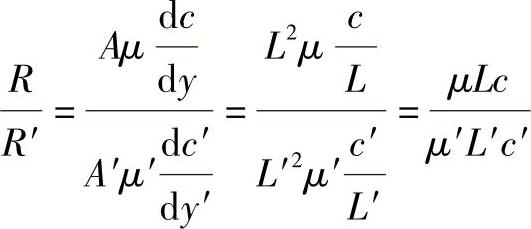
且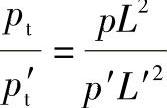

因为

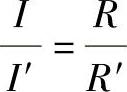
所以

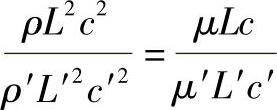
变换后，得

或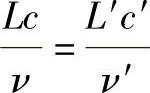

式中 ν——运动粘性系数。

令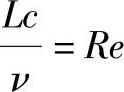

则 Re=Re′。

Re叫做雷诺数，是一个量纲为一项。因为它是用来表征动力相似的，所以称为相似准数。同理，因为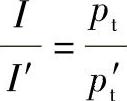

所以

变换后，得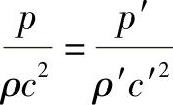

令，则E_u=E_u′

Eu叫做欧拉数，是通风机相似中的另一个相似准数。