导叶环的计算与设计

通常需要在转子前面或后面加装导叶环。问题是将气流折向与叶轮转向相同的方向还是相反。今把设计导叶环所需的知识叙述于下。

置于叶轮之前的导叶中的流动是加速流动。对透平的研究表明，对这种收敛叶栅，作为初步近似，可以忽略有限叶片数的影响。我们在此推荐这种方程式，对经常使用的圆柱形不扭的直叶片，可按中径进行设计。至于后置导叶，问题就在于如何确定气流落后角。一般只在叶片的出口角处考虑落后角。在实用上，叶片的进口角常取为叶轮出口处速度三角形中c₂与u的夹角。计算落后角时可以采用前面讲过的方法。

由速度三角形可以求出叶轮前、后绝对速度的方向。现在的问题把这些有限数目的叶片如何安置才能达到所希望的气流折转角。一般说来，导叶所处的地位比动叶恶劣。因为此时不存在使边界层加速的离心力。为此，必须力求尽可能地降低导叶的负荷。反作用度τ=Δp_st/Δp_tot指出了在动叶轮中和导叶环中所产生的静压各占多少。一般的单级轴流通风机中反作用度不希望低于0.7。轴流压气机中的导叶环则是一个例外。对这种情况，反作用度大致选为0.5。压气机上导叶的作用与单级轴流风机上的不同，不能相提并论。所以，对单级轴流风机，上面推荐的是合适的。设一导叶叶栅将气流由α₁角折向α₂角，叶片的出口角必须有所增加，即α₃＞α₂。此时，气流速度的周向分量c_u应当增加一Δc_u值。根据以前的计算，得到

对前置导叶轮和后置导叶轮这两种最重要的情况，公式（4-126）分别表示为前置导叶轮：

后置导叶环：

可按公式a/t=2.5sin²α₂×（cotα₁-cotα₂）考虑最佳栅距，由此可得前置导叶：

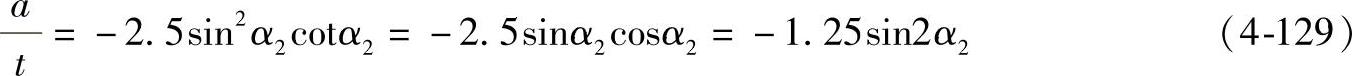
后置导叶：

将它们代入公式（4-129）和公式（4-130），得前置导叶：

后置导叶：

这就表明，若考虑了最佳栅距，气流落后角是一常数，且近似地等于6°～7°。

运用公式（4-132）计算角α′₁=75°、60°和45°三种后置导叶，并将结果画在图4-46上。当叶片间相距较运，且α′₁=75°时，用弧立翼形理论进行计算，估计也能得出同样的结果。经过核算得Δα≈5°，与上述结果十分一致。

与上述简单的设计方法无关，亦可应用魏尼希的方法来计算。

（1）带缝隙的导叶 菲克特的试验证明，加了缝隙以后可以改善固定式扩压叶栅的性能。通常，缝隙的宽度为前机翼弦长的（6～8）%较为有利，如果前机翼弦长的重叠度为（1～2）%的话。此时，导叶可以承受c_a=1.2的高负荷，而没有缝隙的一般导叶c_amax只有0.7。在一些设计中，以间距一半互相错开排列的这种叶片配置是无效的。

（2）前置导叶方案和后置导叶方案的比较 常常会碰到是选用前置导叶好还是后置导叶好的问题。在很多场合，此问题的解决常取决于装置型式和总体布置。除此之外，当然，主要要看哪种结构方案有较高的效率。初看起来，前置导叶似乎是有利的，因为它是加速流动，而后置导叶却是减速流动。但是，这种优点被随之带来的缺点所抵消。因为在前置导叶环中造成的静压降必须在其后的动叶轮中将相对速度减小以取得额外的静压补偿。因此比起后置导叶环方案来损失也就更大些，虽则在动叶轮和导叶轮中都要提高静压。现在的问题就在于采用前置导叶的利和弊哪一个更大些。马西诺夫斯基援引了很多例子很透彻地研究了这个问题。得出的结论是：前置导叶只适用于轮毂比很小且升阻比特别差的场合。此结论只能应用于动叶轮后气流是无旋的情况。也就是说，只在设计点才正确。此外，还假定设计流型是等环量的。这样看来，工程实践中惯用的动叶轮带后置导叶的设计方案一般来说是正确的。

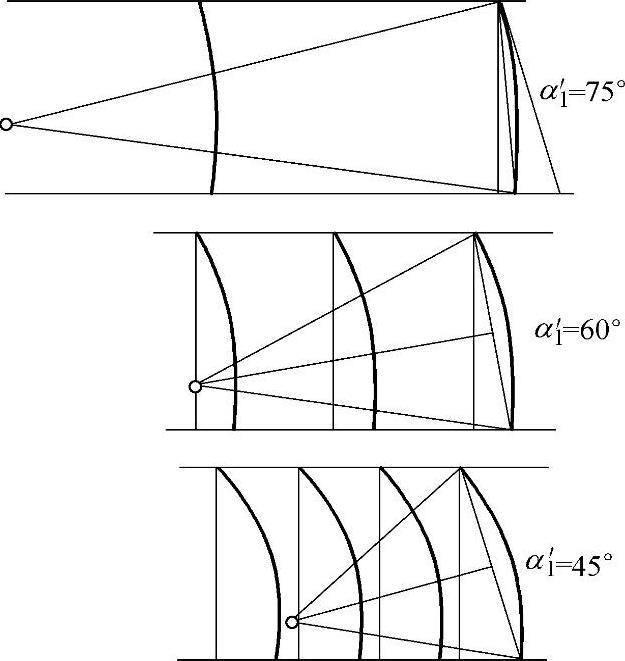
图4-46 三种不同进口角度的后置导叶环（考虑了气流落后角和最佳栅距）

（3）出口角等于常数的前置导叶（柱面形叶片） 为了便于制造加工，提出一个饶有兴趣的问题，即能否采用出口角等于常数的前置导叶？这样也许能设计出一种简单的圆柱形叶片，它是不扭曲的。

任何情况下的旋转流动可以通过一个不变的旋转角α而给定，且这种流动能够容易地求得。假定伯努利方程仍有效，并从该方程P=p+（ρ/2）c²出发，这就意味着所有流线上的能量是相等的。所以总能量在dr方向的变化等于零，即

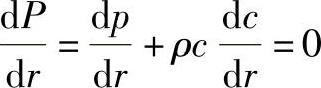
由于c_u分量的存在，就会产生离心力，此力只能为沿径向变化的静压力所平衡。其间的关系为

将此式代入公式（4-133），得

(www.xing528.com)

只要流动遵守伯努利方程并满足垂直于流动方向的径向平衡条件，此微分方程总是成立的。α=常数的假定指的是在所有半径上速度c以同一α角流出。因c=c_u/cosα，故得

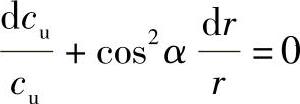
积分并简化之：

这样，流动不再遵顺c_ur=常数的规律。又因c_m/c_u=tanα=常数，公式也可以用c_m分量表示出来。

所以，c_m不再等于常数，而是从外向里递增。图4-47上给出了α=30°的c_m分布曲线。

c_u=常数的旋绕分布规律此处旋绕分量c_u为常数，方程可积分。因c²=c²_u+c²_m；d（c²）=d（c²_m），故得

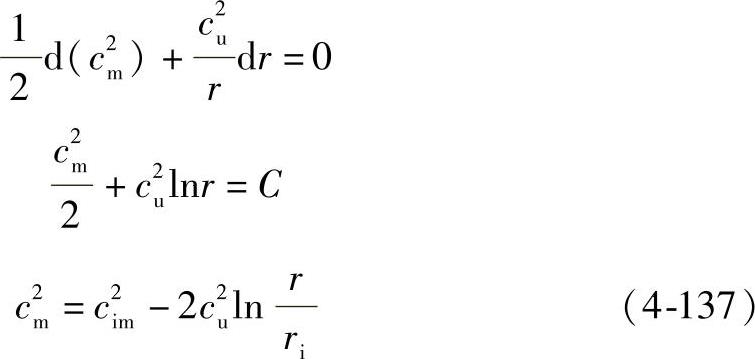
从公式（4-137）可见，在这种情况下，朝着轮毂方向c_m也是增加的。

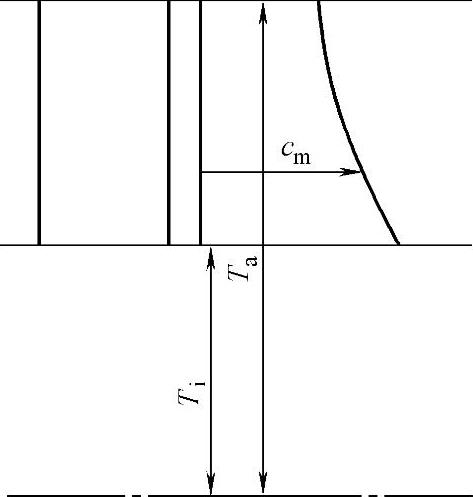
图 4-47

α角的表达公式也很易导出，只要在公式4-137等号两边同除以c²_u，则得

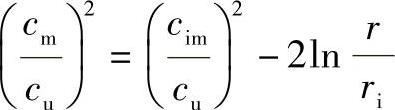
因c_m/c_u=tanα，就有

α角的值向外递减。所以此种流型给出的叶片扭曲规律与标准的c_ur=常数的相反。

通用指数旋绕分布规律假设c_u按c_u=C′/rⁿ的指数规律分布，方程也是可积分的。将c_u=C′/rⁿ代入通用公式（4-134），可得cdc+（C′²/r²ⁿ⁺¹）dr=0。积分后得

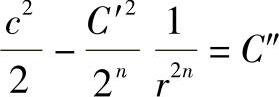
令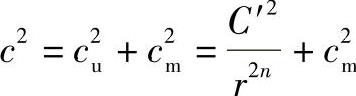

就有

现在按n是等于、大于还是小于1区分为三种不同的情况：

n=1c_m=c_im（标准情况）

n＞1c_m＞c_im

n＜1c_m＜c_im值得注意的是在这些解答中，也能实现c_m＞c_im的流动情况。

这些结果很有意义。它指出，借助于转动的前置导叶可以实现单级轴流风机的调节。在无旋轴向进气情况下，可能是为了降低流动阻力的缘故，通常采用一种非扭曲无弯度的前置导叶。设叶片结构是弹性的，现仅扭转它的尾部，便形成一个柱状的前置导叶，此时它所产生的气流旋转角等于常数。在大多数情况下，只有与转动方向相同的正旋绕才有实际意义，因为差不多只有这种情况才有良好的调节效果。对简单的无预旋的轴流叶轮，当流量低于额定值时，轴向速度c_m的分布是向外递减的。人们认识到，在这种情况下，柱状前置导叶是完全适用的。进而提出了这样一个问题：扭曲叶片是否一定有益？

如前所述，毫无疑问可借助于前置导叶的适当形状而获得其他形式的c_m分布。当前置导叶安装在喷管状的，或外壁呈曲线形的进气区域中时，这些型式的c_m分布是很有用的。