损失与效率分析：4.6轴流通风机

在轴流通风机中，气流经过叶片环时的损失很复杂，它沿叶片高度的分布很不均匀。这种损失的不均匀性可由试验数据或通过计算得到。目前在轴流通风机设计中，有的已经考虑了损失分布的不均匀性。为便于计算，通常把分布很不均匀的损失沿叶片高度均摊。这样，只需计算平均半径处的损失就可以了。

通风机的损失大小可用效率来衡量。单级轴流通风机的流力效率可通过公式（4-52）计算：

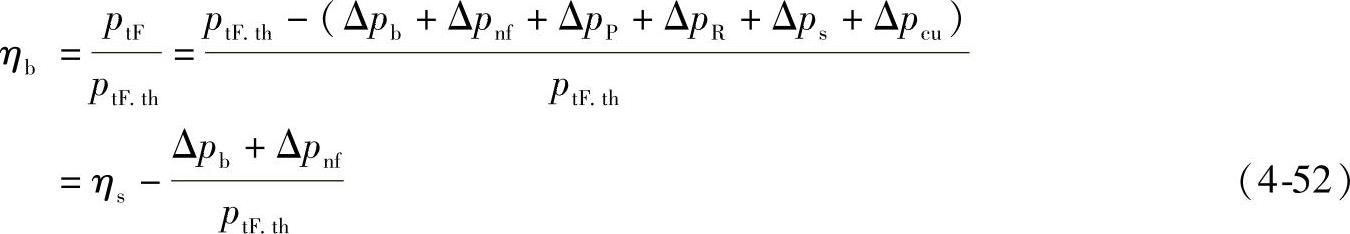
式中 p_tF.th——轴流通风机的理论全压（Pa）；

Δp_b、Δp_nf、Δp_P、Δp_R、Δp_s——分别为通风机入口集流器、流线罩、前导流器、叶轮及后导流器的压力损失（Pa）；

Δp_cu——级中最后一个叶片环出口的旋绕能量损失（Pa）；

η_s——级效率。

在轴流通风机的气动计算中，有时把级效率_ηs作为通风机的全压效率η_tF。上述公式中有关损失可以通过相应的损失系数计算。在轴流通风机气动设计中所需的通风机全压效率η_tF，可以通过两种途径得到。一是参考已有轴流通风机的η_tF-n_s曲线得出；另一种是通过计算得出。本手册采用的是前者。因此，对有关损失的计算方法这里不做详细介绍。但是应指出，气流经过叶片环的总损失系数C_xc与叶栅稠度τ、叶片数Z、毂比d、升力系数C_y（或C_yc、C_G）、相对径向间隙δ-_r等有关。因此，在轴流通风机设计时，对于这些参数的选择与计算要给予充分的重视。

在通风机中还有一些辅助部件，例如进气箱、进气弯道、扩散器及轴承支座等。考虑这些损失所计算出来的效率，称为通风机装置效率_ηP。它可由公式（4-53）计算：

η_P=η_tF（1-ζ_Pσ） （4-53）

式中 ζ_P——通风机装置损失系数；

σ——通风机动压p_dF与通风机装置压力p_P之比，即σ=p_dF/p_P；p_P为通风机全压p_tF与通风机装置的压力损失Δp_P之差，即p_P=p_tF-Δp_P。

考虑摩擦力的计算。叶片和有时可能接入的扩压器中存在着损失，这种损失用相应地提高压力Δp的办法加以考虑。令η为风机的总效率，风机叶片必须产生更高的压力，即Δp/η，于是就有公式（4-54）：

由于效率的影响，叶片所产生的压力应加大至Δp/η，这样，

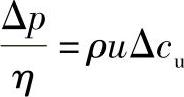
则这就是为产生压力Δp实际上所需要的Δc_u之值。

在前面导出的一些公式中考虑损失，可得下面最后的实用公式：

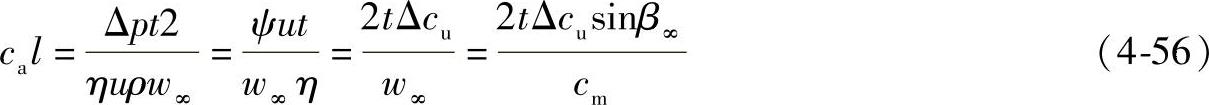
将Δc_u=w₁cosβ₁-w₂cosβ₂代入，得

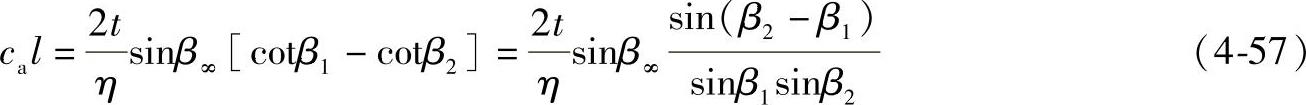
然而，按各类损失区分效率很重要，以便对设计中各种措施的影响有一概括的了解。

通过下述计算能够得到一个简略的梗概。

首先让我们更细致地考察一下叶轮的摩擦损失。在图4-21中沿w_∞方向出现阻力，阻力作的是消耗功，它导致压力有一Δp′的损失，兹计算如下：若每秒钟内流经叶片通道的容积流量为V=c_mtb，则

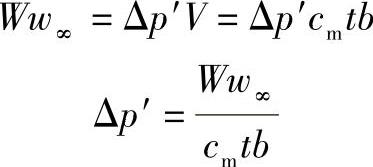
由孤立翼形理论公式W=c_wqF并作相应代换后得

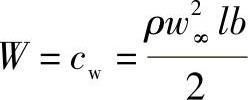
这样

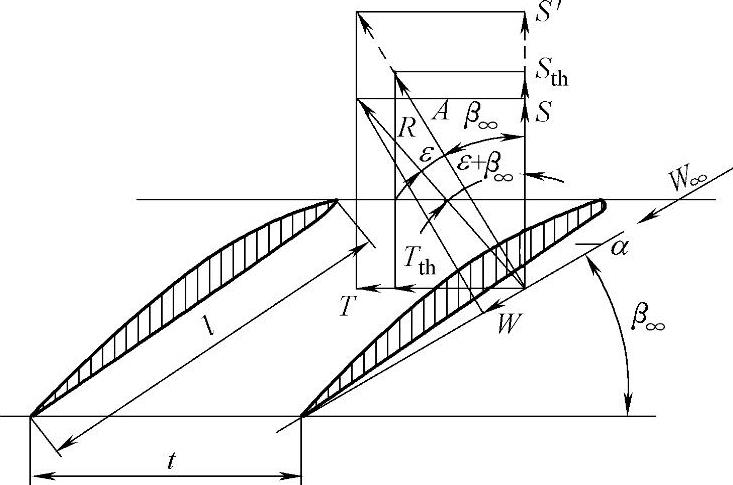
图4-21 考虑摩擦时作用在叶栅翼形上的作用力

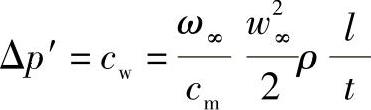(www.xing528.com)

将此损失与全压力计算公式相比较，则

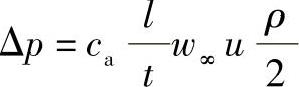
损失所占的百分比为

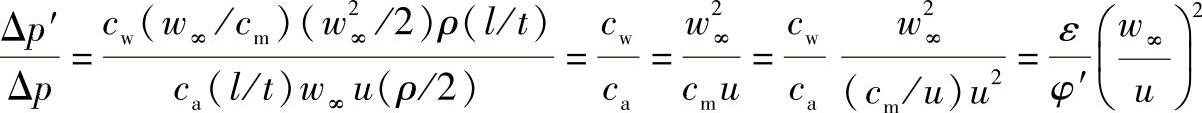
在轴流式通风机中一般速度三角形很扁平，初步可以认为w_∞≈u。此时损失的百分比为

直接从叶片做功出发，也可以达到我们的目的。若仍以Δp代表总压力，它所消耗的功就是ΔpV=Tu。从图4-21得T=Rsin（β_∞+ε），且因V=c_mtb，则

Δpc_mtb=Rusin（β_∞+ε）

若仍使用等式，Δp=ρuΔc_u和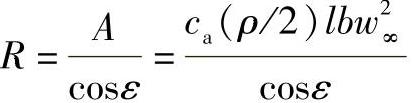就会得到：

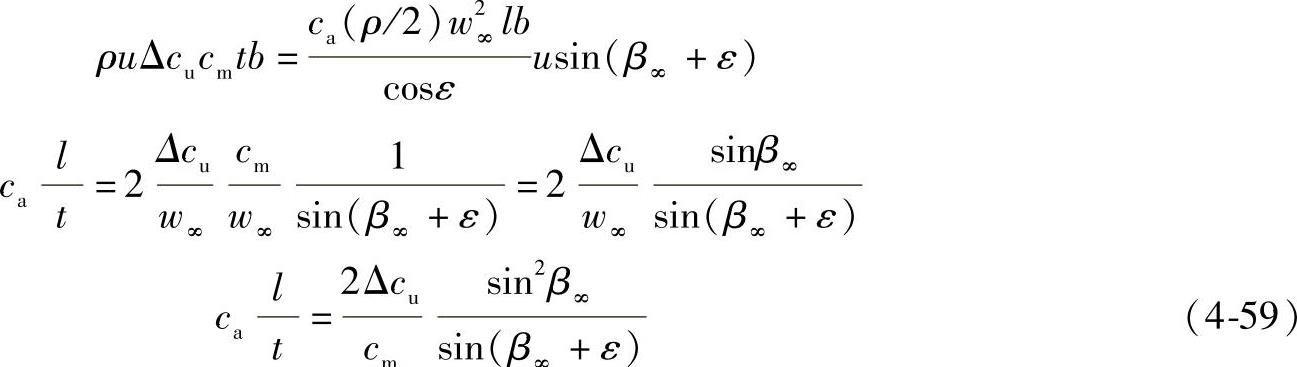
若在公式（4-59）中保留Δp项，可得

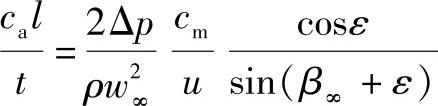
当ε≈0时，则

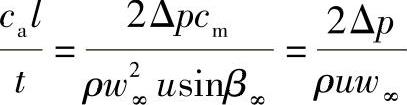
通过下面的分析，会深化我们对问题的认识。在图4-21中首先将合力R分解为沿升力作用方向的力A和阻力W。其次把它分解为沿叶栅轴线方向的切向力T=Rsin（β_∞+ε）及垂直于叶栅轴线方向的所谓推力S=Rcos（β_∞+ε）。

两者之比值是

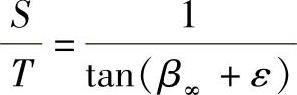
现在我们就来看无摩擦时该比值的大小。显然有以下等式：

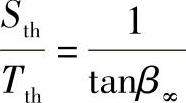
如果为了求得比较两种情况的简单式，由于相似，我们假设切向力相等，得

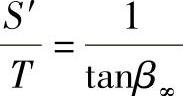
只要假设没有摩擦，就可算出理想推力。这样，也就容易计算出实际推力与理想推力之比。轴向推力对静压差的产生有决定性的意义，所以也就很自然地把它们的比值当作静压效率。于是可写

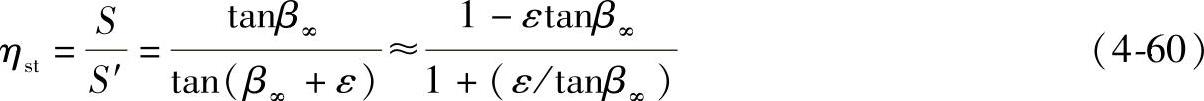
这就是从空气螺旋桨理论导出的公式。对空气螺旋桨，有用的只是这项推力，而那些力的切向分量等都不重要。在评价空气螺旋桨时，这种效率的大小是唯一有用的根据。效率的最大值为η=tan²β_∞。

也可用实测得到的静压差p₂-p₁与理论静压升作比较而得到静压效率。理论静压力用公式（ρ/2）（w²₁-w²₂）求出，其含义就是把相对速度从w₁值无损失地减小到w₂值时带来的静压升高。

滑动角可由公式（4-60）算出：

根据试验数据，还可以用此公式验算滑动角ε。