叶轮子午截面和圆柱叶片型线的绘制

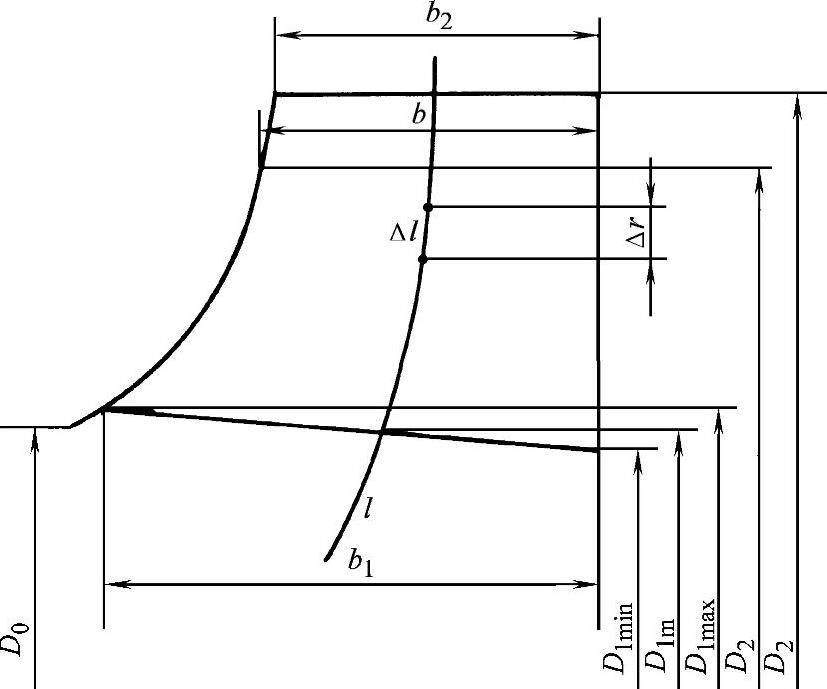
图3-66 叶轮子午截面的绘制

根据前面计算出的D_1m、D_1max、D_1min、b₁、β_1A、D₂、b₂及Z等数值，就可绘制出叶道的子午截面及叶片型线。

叶轮子午截面的形状可根据入口速度c′_1m均匀地变化到c′_2m的原则来绘制。不同直径的叶片宽度b可按公式（3-178）决定：

式中 D——叶片的任意直径；

c′_m——不考虑叶片厚度时，任意直径处的气流子午速度；

μ——任意直径处的有效气流充满系数，其值可根据从μ₁均匀地变化到μ₂的原则决定。

连接不同b值的端点，即可得出前盘的形状。另外，再根据叶片入口的不同直径，可绘制出叶片始端在子午面的投影，如图3-66所示。不同宽度中点的连线l称之为中线。

在设计中，如果采用锥形前盘，则以直线连接b₁及b₂的两端。

下面介绍圆柱叶片型线的绘制。

叶片整个表面与后盘成直角的叶片称为圆柱叶片。叶片型线的绘制原则是：在保证最佳当量扩张角θ_eq条件下，使相对速度w₁逐渐地变到w₂，以减少叶道中的损失。此外，叶片也不宜过长，否则将增加摩擦损失。由于气流的相对速度w及子午速度c_m是逐渐变化的（见图3-67）。于是，不同半径处的叶片安装角β_A也是由β_1A逐渐地变化到β_2A。这些条件可保证流道截面积逐渐地变化。

把叶片入口与出口间的中线分成许多等长度的线段（见图3-66）。然后，可以从叶轮子午面上得出分点的半径R。以l及R为横坐标，相对速度w及子午速度c′_m为纵坐标（见图3-67）。画出w₁、w₂及c′_1m、c′_2m，并分别以直线连接，即可得出不同R处（或不同l处）的相对速度w及子午速度c′_m。

由任意半径处的速度三角形可得出：

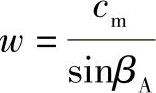
且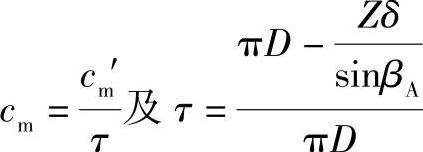

于是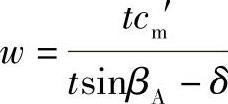

从而得出任意半径R处的叶片安装角度β_A：

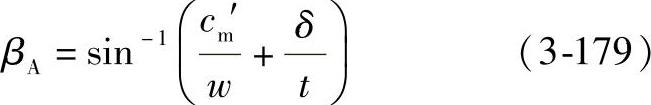
式中 c′_m——在半径R处流体质点的子午速度；

w——同一半径R处的相对速度；

δ——叶片垂直厚度；

t——栅距，。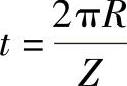

叶片厚度δ从强度角度考虑。除机翼形叶片以外，其他型式叶片一般为等厚的。因此，不同半径处的叶片厚度δ=常数，如图3-67所示。

当中线l几乎是径向时，可以忽略中线基元长度Δl与半径增量ΔR的差别。

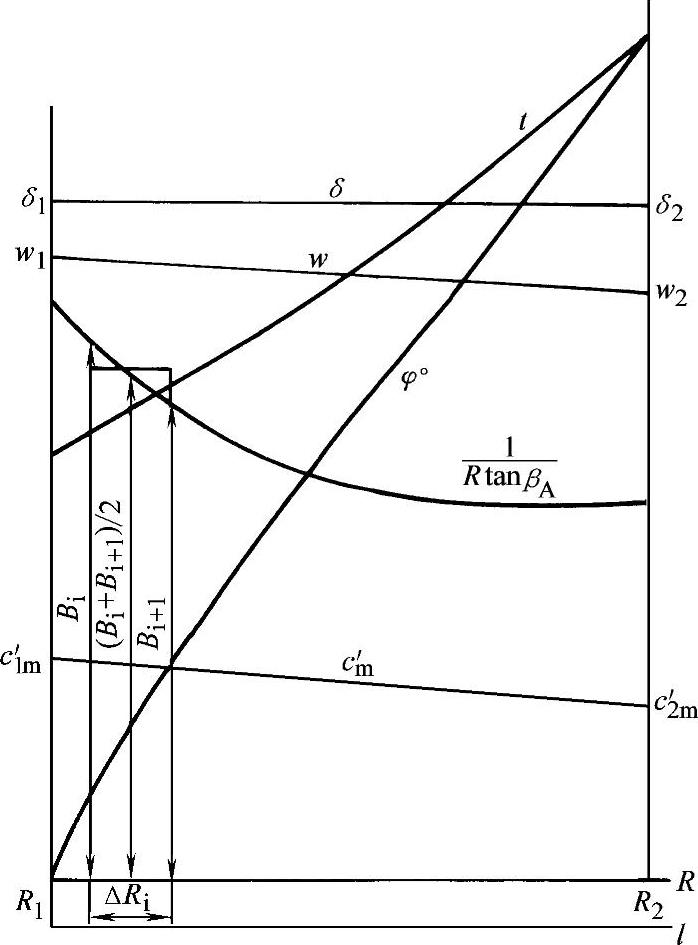
图3-67 求R与φ间的关系用图

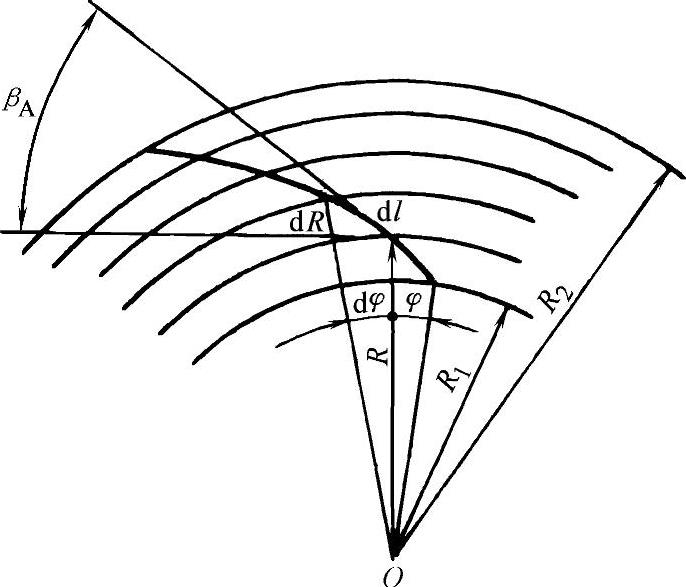
图3-68 求φ-R间函数用图

通过计算得出不同半径的栅距t、叶片角度β_A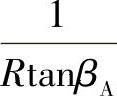及后，将t及值画于图3-67上。接着可绘制叶片的型线。型线绘制方法有逐点画法及多圆弧画法等。

1.逐点画法

如果流体质点沿中线移动一基元长度dl，相应半径的基元增量为dR，图3-68中心角的基元增量为dφ。中心角φ与半径R间的微分方程为

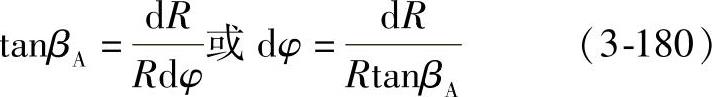
于是中心角增量为

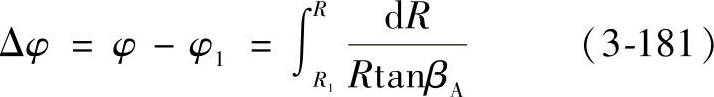
式中 φ——任意半径R处的中心角；

φ₁——半径R₁处的中心角。(www.xing528.com)

令半径R₁处的中心角φ₁=0，则公式（3-181）可写为

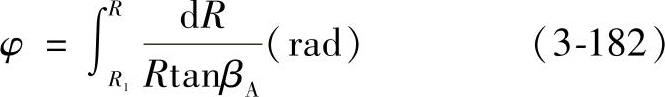
如用度数表示，公式（3-182）则为

一般可用图解法或表格形式求出φ与R间的关系。令被积函数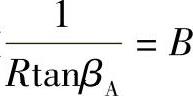，则中心角增量Δφ_i为

式中 ΔR_i——半径增量；

B_i及B_i+1——分别为所研究线段的开始及终了处被积函数的数值。

它们的总和则为

利用公式（3-184），半径每有一增量，即可得出一个中心角φ。于是可画出R与φ间的关系曲线（见图3-67）。利用所得的R-φ关系，可画出叶片的型线。然后再画上叶片厚度，就可得到叶片在平面投影图上的轮廓。

2.多圆弧及单圆弧画法

用逐点法绘制叶片型线比较麻烦，为方便起见，有时采用多圆弧，甚至单圆弧画法。多圆弧画法，就是用许多共轭圆弧来绘制叶片型线，如图3-69所示。首先在R₁与R₂之间画几个同心圆，例如3～4个。根据前述的方法，利用图3-67得出各半径处的叶片安装角β_1A、β_BA、β_CA、…、β_2A。随后用图3-70求得各圆弧的半径ρ_A、ρ_B、…、ρ_D。图3-70中的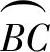为图3-69图中多圆弧的一段。M为圆弧BC的圆心。在△OBM中应用余弦定律可得

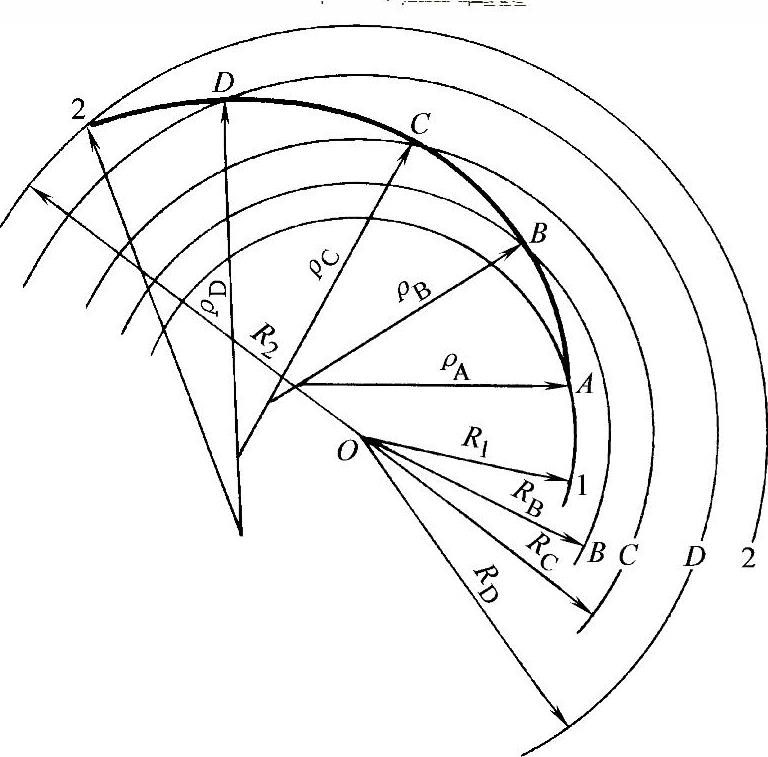
图3-69 用多圆弧绘制叶片型线

图3-70 圆弧叶片的绘制

又在△OMC中，应用余弦定律可得

从公式（3-185）及公式（3-186），可得出绘制圆弧BC的半径ρ_B为

圆弧叶片的圆心，位于半径为OM的圆周上。由公式（3-185）可得

用相同的方法，可画出其他各段圆弧，从而得出整个叶片的型线。

如果整个型线只用一个圆弧绘制时，称这种画法为单圆弧法。这种叶片型线简单，制造容易，所以用得比较广泛。但其流道内速度变化的均匀程度不如用逐点法所绘成的叶道。在这种叶道内，气流甚至时而减速时而加速，将产生局部旋涡，增加损失。因此，为提高通风机效率，需对叶道面积沿中线的变化进行审查（见图3-71）。如果截面积变化很不均匀，则需对叶片的型线及前盘的轮廓进行修正。

所设计的叶片为平板叶片（见图3-72）时，在△OAB中应用正弦定理可得

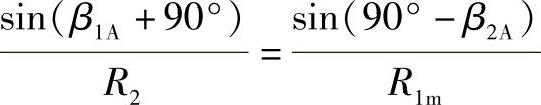
即R_1mcosβ_1A=R₂cosβ_2A （3-189）

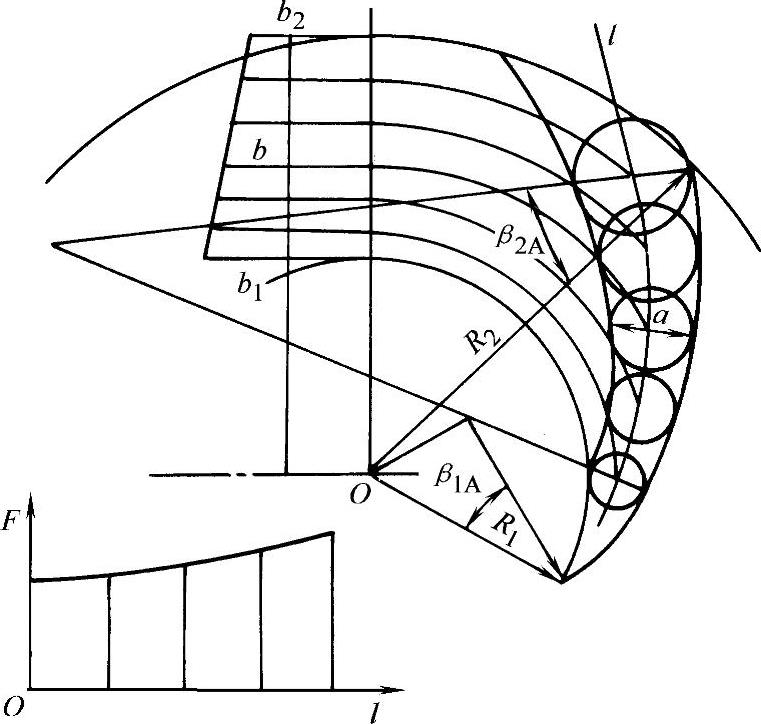
图3-71 双圆弧叶片流道面积F沿中线l的变化

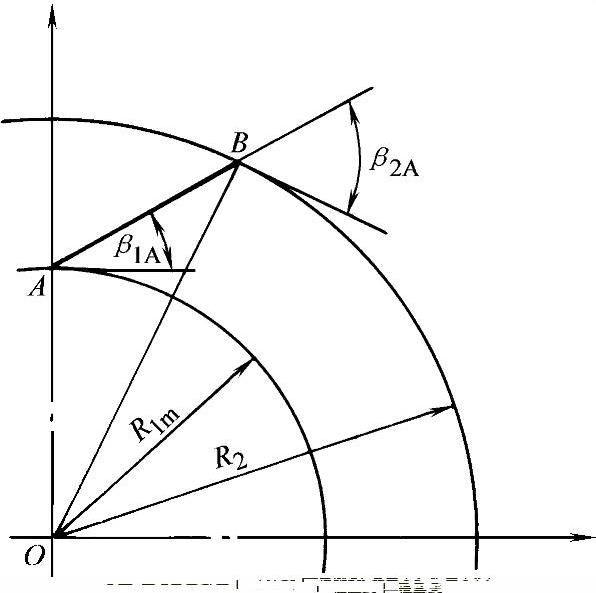
图3-72 平板叶片的绘制

这时，R₁、R₂、β_1A和β_2A四个参数不能都任意选定。可按前述方法，先决定出R₁、R₂及β_2A，而后用公式（3-189）决定叶片入口角度β_1A。

平板叶片型线的绘制方法简单，制造也容易。但流道面积沿中线l的变化规律不好，叶道内流力损失较大，通风机效率低。为弥补这缺点，可用前述方法，对叶轮的前盘轮廓进行修正。