如何确定叶轮入口直径？

在决定叶轮入口几何参数以前，先分析入口的气体流动情况。

气流沿轴向进入叶轮时，有时产生附面层分离，使气流有效截面积减小。气流流过叶轮的流量q_sc为

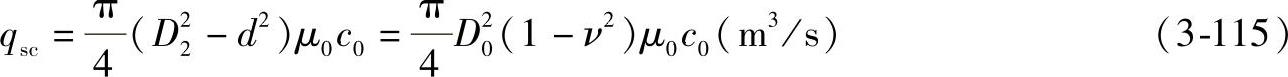
式中 D₀——叶轮入口直径（m）；

d——叶轮入口轮毂直径（见图3-45a）（m）；

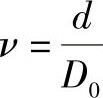，无阻碍入口（见图3-45b）时ν=0；

c₀——叶轮入口处的气流轴向速度（m/s）；

μ₀——叶轮入口气流充满系数，一般μ₀=0.9～0.95，采用优良的弧形进风口时，μ₀=1；一般q_sc按下式计算：

q_sc=（1.02～1.05）q_s

式中，q_s为通风机流量，1.02～1.05为考虑叶轮与进风口间的间隙失的系数。

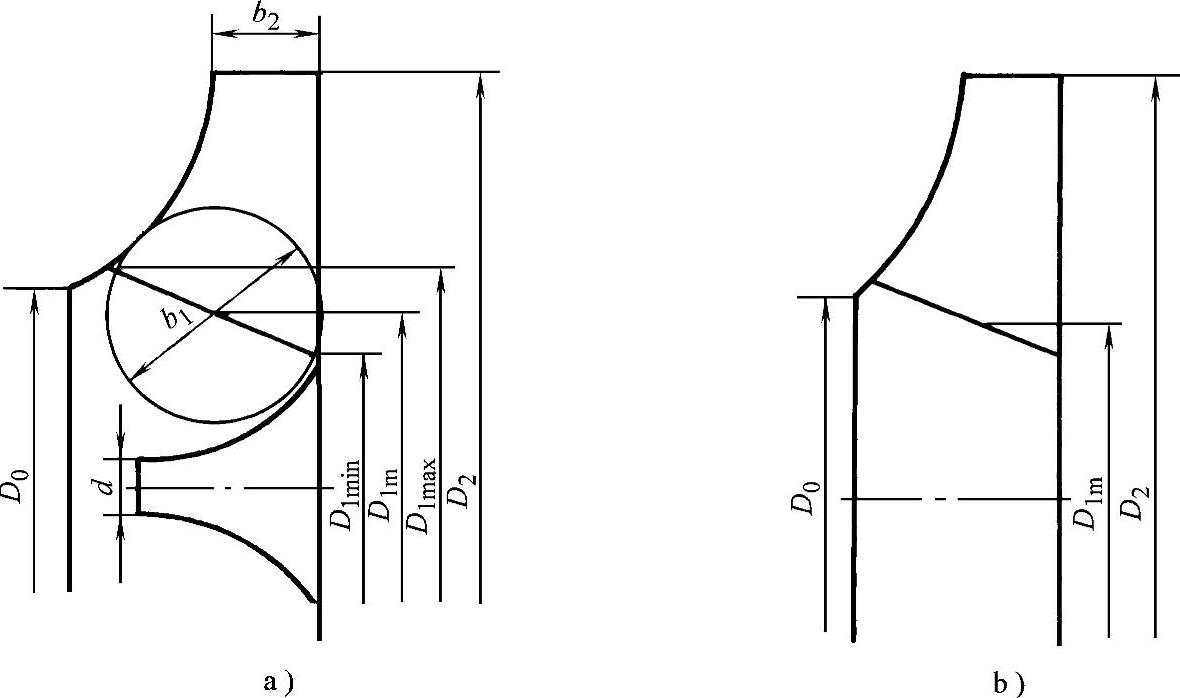
图3-45 决定叶轮基本尺寸用图

a）叶轮入口有阻碍 b）叶轮入口无阻碍

当ν=0时，公式（3-115）可写成：

气流由轴向变为径向时，也会产生分离，流过叶轮的体积流量为

q_sc=πD_1mb₁μ₁c′_1m （3-117）

式中 D_1m——叶片入口的平均直径（m）；

b₁——叶片入口宽度（m）；

c′_1m——叶片入口前气流的子午速度（m/s）；

μ₁——叶片入口前气流充满系数，对平前盘，μ₁=0.8～0.87；对锥前盘，μ₁=0.83～0.91；对弧形前盘，μ₁可达0.95。

凡速度符号带上标“′”者，为刚流到叶片入口边缘而尚未流入叶片的气流速度，不带上标“′”者为进到入口边缘以后的气流速度。

在没有前导器的条件下，可认为气流没有旋绕速度，即c′_1u=0，此时c′_1m=c′₁。当气流刚进入叶片以后，由于叶片有一定厚度δ₁，致使流道截面积缩小，气流子午速度由叶片入口前的c_1m′增加到c_1m，如图3-46和图3-47所示。β′₁为未进入叶片前的气流角，β₁为进入叶片以后的气流角。叶片入口气流冲角为叶片入口角β_1A与β′₁或β₁之差，分别用i′或i表示。

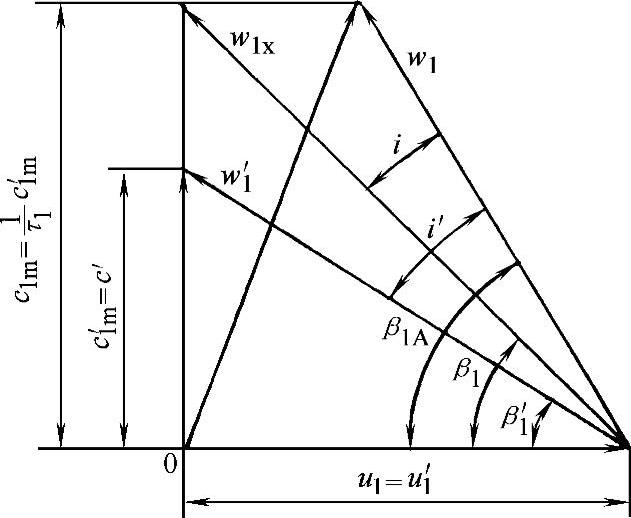
图3-46 叶片入口前后的速度三角形

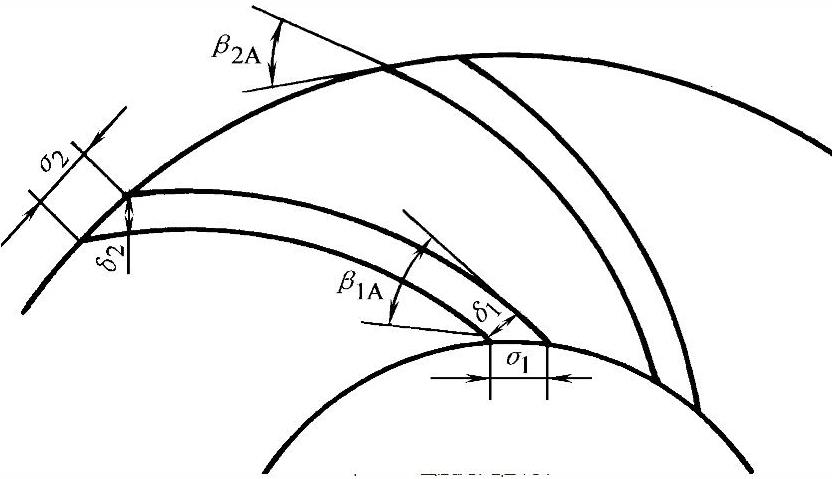
图3-47 叶片的入口和出口

假定叶片入口前后气流充满系数相同，则得

q_sc=（πD_1m-Zσ₁）b₁μ₁c_1m=πD_1mτ₁b₁μ₁c_1m （3-118）

式中 Z——叶片数目；

σ₁——叶片在入口圆周上的厚度（m），；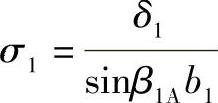

τ₁——叶片入口断面收缩系数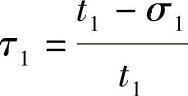，；t₁为叶片入口的栅距（m），。

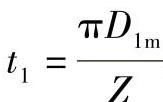由公式（3-118），得

对比公式（3-117）和公式（3-118），可得

c′_1m=τ₁c_1m （3-120）

在叶片入口边缘后，还有下列关系：

q_sc=w₁（πD_1msinβ_1A-Zδ₁）b₁μ₁ （3-121）

由此可得叶片入口后的平均相对速度：

当叶轮入口气流不受阻碍时，由公式（3-116）及公式（3-117）可得

式中 K_c——叶轮入口截面积与叶片入口前截面积的比值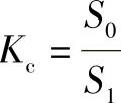，，其中。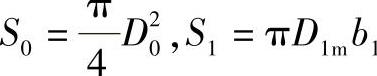

气流从叶轮入口到叶片入口应该加速还是减速，存在不同的看法。有人主张，为了减少气流拐弯时的分离，应是加速运动，即

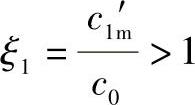
有人认为，为了减小叶道内的损失，气流应该减速。现在大量高效率离心通风机的统计数字如图3-48所示。图中的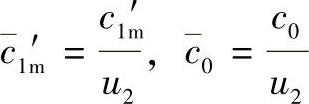。由图可看出，大部分情况下：

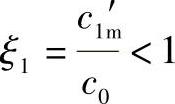
有关后向高效率离心通风机的统计资料表明，通风机的效率η与面积比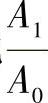有密切关系，如图3-49所示。由图可看出，当η>80%时，叶片入口截面积A₁远大于叶轮入口截面积A₀。

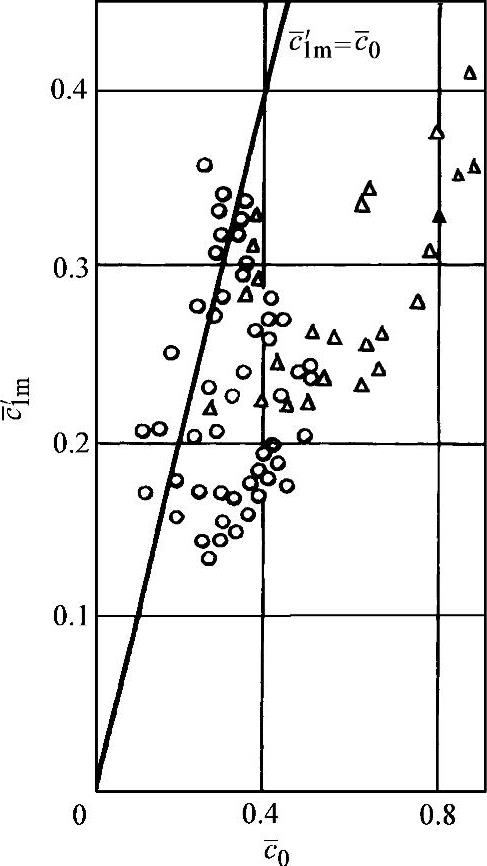
图3-48 额定工况下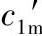与的关系

设计中，除上述资料可作参考外，还可用公式（3-124）计算ξ₁：

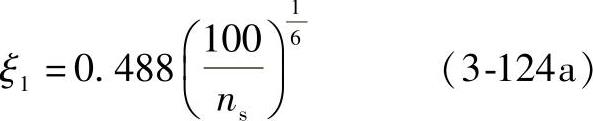(www.xing528.com)

或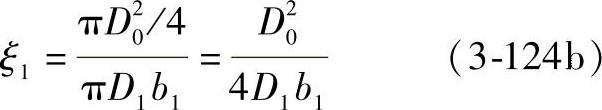

叶轮设计中，在没有前导器的情况下，叶轮入口前是否考虑旋绕速度c′_1u也有着不同的看法。

对于叶轮入口直径D₀，在大多数情况下，D₀=D_1m，即使两者不等，也相差不大。所以设计时按两者相等来考虑问题。

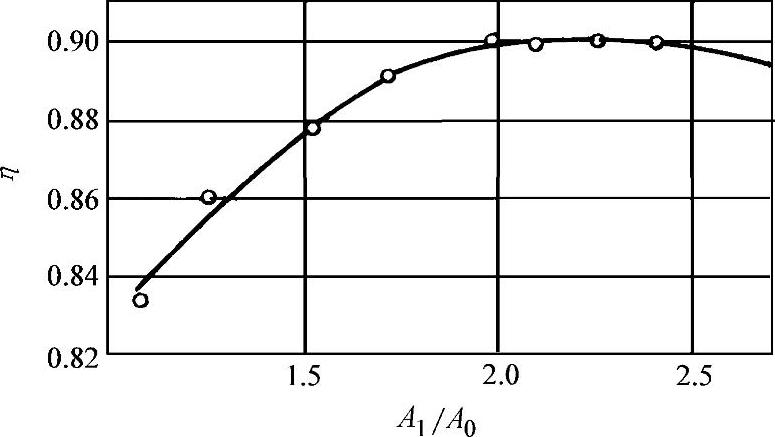
图 3-49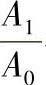与通风机最大效率的关系

叶轮内的流力损失主要发生在叶道内，而叶道内损失的大小，主要与叶片入口后的平均相对速度w₁的平方成正比。w₁值最小时，损失应最小。根据此原则来决定叶轮入口直径D₀。

假定气流入口冲角i=0。从图3-46可得

w²₁=c²_1m+u²₁ （3-125）

当D₀=D_1m时，从公式（3-120）和公式（3-117），得

将公式（3-126）代入公式（3-119），得

叶片入口圆周速度为

式中 ω——叶轮角速度（1/s）。

将公式（3-127）和公式（3-128）代入公式（3-125）中，得

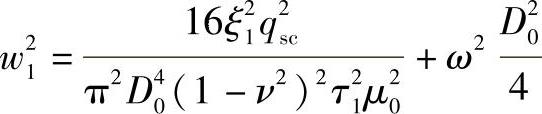
在q_sc、ξ₁、τ₁、ν和ω一定的条件下，可根据下式求出w₁值最小时的D₀值：

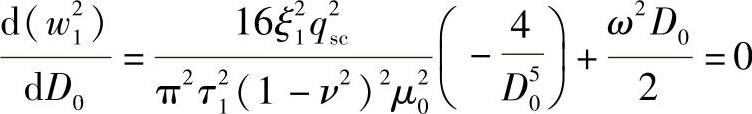
化简后，得

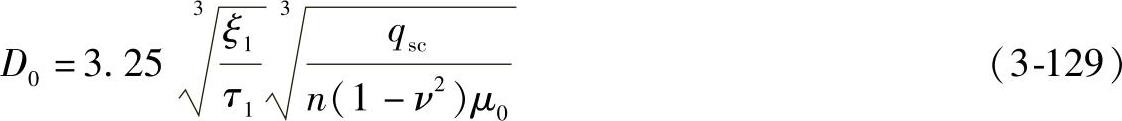
式（3-129）是从气流在叶道内损失最小考虑的。除此以外，在叶轮中还有其他损失：如气流在叶轮入口，由于气流的分离而产生的损失；气流转弯的损失等。所以，式（3-129）在实际应用中有一定的局限性。

亦可用式（3-130）决定叶轮入口直径D₀：

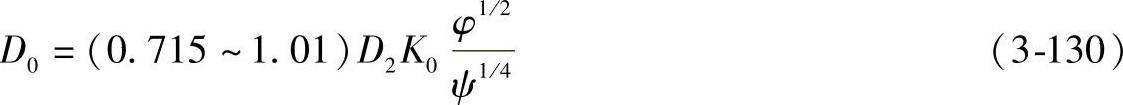
式（3-130）中系数K₀与D₀有关，见表3-10。在已知D₂、φ、ψ条件下，利用公式（3-130）与表3-10，经过反复试算，可最后决定出叶轮入口直径。

表3-10 K₀与D₀间的关系

最佳收敛性系数ξ_1opt（即最佳速比）：

式中 D₁——D₁=D₁/D₂；

A——A=；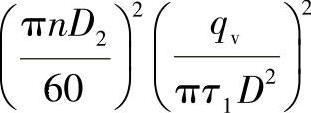

B——系数，与流量系数φ有关，如图3-50所示。

公式（3-131）说明，最佳收敛性系数ξ_1opt并不是一个常数，它随流量系数φ及直径比D₁/D₂而变化。图3-50b是按公式（3-131）所绘出的曲线，取τ₁=0.9。

从图3-50b中可看出：

1）最佳进口是收敛还是扩散，首先取决于流量系数φ。当φ＞0.1时没有收敛区，即无论D₁/D₂取多少，都应设计成扩散型进口。当φ＜0.1时，有收敛区也有扩散区，是否把叶片进口设计成收敛形还是扩散型还取决于直径比值D₁/D₂。

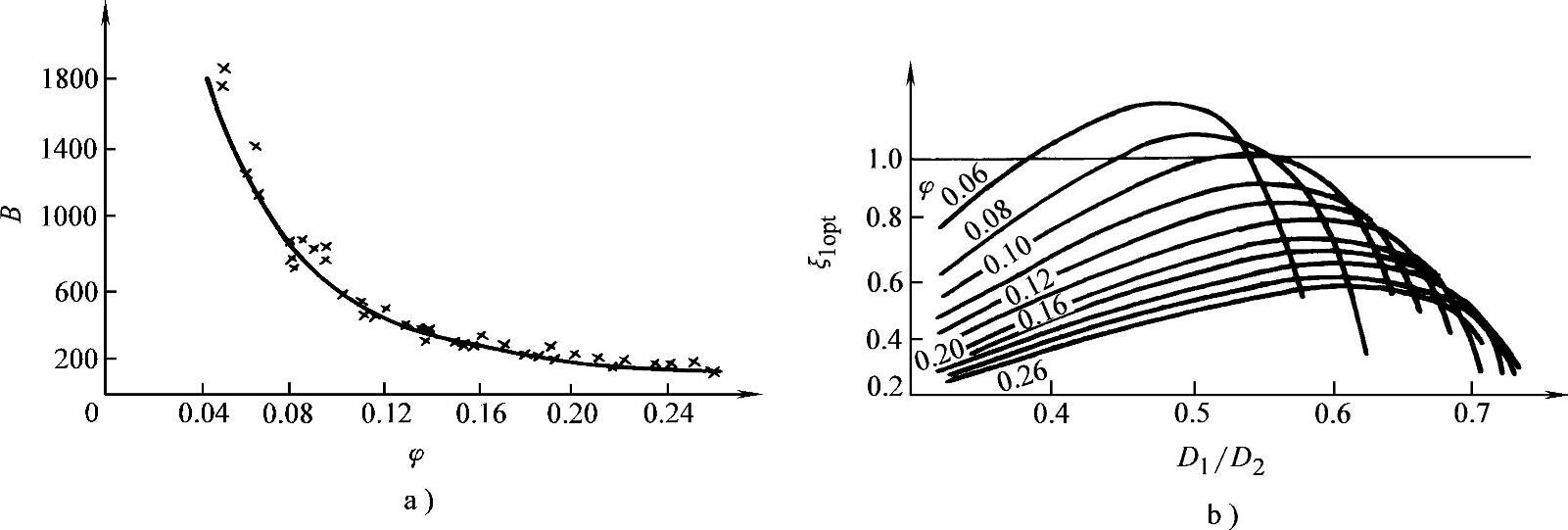
图 3-50

a）系数B与φ的关系 b）ξ_1opt=f（φ，D₁/D₂）关系

2）随着φ的增大，进口扩散程度要求越大。相应地大比转速风机应设计成扩散型进口。

3）进口设计时，先求出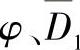，然后按公式（3-131）（见图3-49b）求出最佳收敛性系数，完成叶轮进口设计。

亦可由流量方程得

式中 q_v——容积流量（m³/s）；

c₀——叶轮进口速度（m/s），可按表3-11选择；

d——轴径（m），对悬臂式叶轮d=0，对双支撑叶轮，d=（0.15～0.25）D₂。

表3-11 叶轮进口速度范围

D₀/D₂比值见表3-12。

表3-12 D₀/D₂值范围