离心通风机的特性曲线及理论分析

图2-6 叶片数目为无限多时的叶片出口速度三角形

通风机在一定吸气状态和一定转速下工作时，通风机的理论全压与理论流量之间的关系曲线，叫做通风机的理论全压特性曲线。下面就离心通风机进行讨论。

如图2-6所示的叶片出口速度三角形，β_2A为叶片出口角，则

c_2u∞=u₂-c_2mcotβ_2A

代入公式（2-38），得

p_T∞=ρu₂（u₂-c_2mcotβ_2A） （2-41）

通风机出口的子午速度一般为径向，故通风机的理论流量q_r可按公式（2-42）计算

q_r=πD₂b₂c_2m （2-42）

变换后，得

式中 D₂——叶片出口的直径（m）；

b₂——叶片出口宽度（m）。

将式（2-43）代入式（2-41），得

式中 ρ——气体的密度（kg/m³）。

需要注意，这里的u₂是叶片出口的圆周速度，它与叶轮出口的圆周速度是有区别的（一般情况把它们看成相等）。ρ是通风机入口的气体在标准状态下的密度。一定尺寸的通风机在一定转速下工作时，公式（2-44）右边的各量，除q_r以外都是常数，故公式（2-44）可写成

p_T∞=A-Bq_r （2-45）

式中，A=ρu²₂=常数，是流量等于零时的理论全压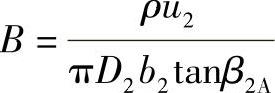；=常数。(www.xing528.com)

在p_T∞-q_T图上，公式（2-45）是一条直线。当其他参数都一定时，此直线的斜率决定于叶片出口角β_2A的大小（见图2-7）。

当β_b2=90°时，离心通风机的理论全压曲线为距横坐标轴ρu²₂，且与横坐标轴平行的一条直线。这时，p_T∞ 不随q_T改变。当β_2A＞90°时，公式（2-45）右边第二项为正，理论全压p_T∞随着q_T的增大而增高，为通过纵坐标轴上同一点向上倾斜的直线。当β_2A＜90°时，公式（2-45）右边第二项为负值，p_T∞随着q_r的增大而减小，理论全压曲线则为通过纵坐标上同一点向下倾斜的直线。

通风机在一定转速下工作时，不考虑任何损失的轴功率（即理论功率）与理论流量之间的关系式，叫做理论功率特性曲线。

理论功率P_T可根据理论压力和理论流量计算，即

P_T=p_T∞q_T （2-46）

将公式（2-45）代入公式（2-46），得

P_T=Aq_T-Bq²_T （2-47）

显然，β_2A=90°时，上式右边第二项为零，理论功率特性曲线为经过坐标原点的一条直线。当β_2A＞90°或β_2A＜90°时，则为经过原点，在该直线上面或下面的抛物线，如图2-8所示。

根据以上分析，离心通风机的叶片出口角β_2A的大小，对通风机的特性起着很重要的作用。所以β_2A角是离心通风机的一个重要几何参数，通常用它来区分叶片的型式。

叶片可分三种型式：①后向叶片，β_2A＜90°；②径向叶片，β_2A=90°；③前向叶片，β_2A＞90°。

图2-7 通风机的理论全压特性曲线

图2-8 理论功率特性曲线

对只是叶片出口角度不同的三种离心通风机的工作情况，作如下分析。

由图2-9中的叶片出口速度图可以看出，后向叶片，c_2u∞＜u₂；径向叶片，c_2u∞=u₂；前向叶片，c_2u∞＞u₂。根据公式（2-36），在u₂不变的条件下，理论全压p_T∞随着c_2u∞的增大而增高。所以在这三种通风机中，后向叶片的全压最小，前向叶片的全压最大，径向叶片的全压则在两者之间。但是，就叶轮反作用度的大小和通风机效率的高低来说，情况恰好相反。因为后向叶片的c_2u∞最小，由公式（2-40）计算出来的反作用度Ω值最大。由图2-9还可看出，后向叶片的c_2∞最小，故在扩压部分能量转换时的损失最小，结果通风机的效率最高。前向叶片的c_2u∞最大，则Ω值最小，结果通风机的效率最低。径向叶片的通风机的Ω值与效率则处于两者之间。由图2-8就离心通风机的超载能力来对比，当通风机的流量增大时，后向叶片通风机的功率增加最慢，前向叶片的功率增加最快，径向叶片的功率则在两者之间，所以后向叶片通风机的超载能力大，前向叶片通风机的超载能力小，径向叶片通风机的超载能力则居于两者之间。因此，大功率的离心通风机，用后向叶片的较多。但是，如果通风机的转速或叶轮圆周速度受一定条件限制，而又要求有较高的通风机全压时，也常选用前向叶片的结构型式。

图2-9 后向、径向和前向叶片的比较