伯努利方程的应用实例解析

1.水静力学基本方程式

有一容器（见图2-2）其静止液面上的压力为p₀；速度为c₀=0；液面高度为Z₀。在液体中任一点上的压力为p；速度为c=0；液柱高度为Z。今将伯努利方程应用于液面和A点。因有H_M=0，h_r=0，ρ=常数，则有

或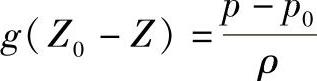

p=p₀+gρ·h （2-26）

式中 h=Z₀-Z，公式（1-26）即为水静力学基本方程式，它表明在液面下任一点的静压力等于液面上的压力p₀与该点上的液柱高度h所产生的压力gρh之和。当p₀为大气压时，取p₀=0，则任一点A的表压力

p=gρh （2-27）

利用公式（2-27）的原理即可制造液柱压力计，即液柱的高度等于所测点的压力。

2.皮托管

如图2-3所示，设有一水槽中有水流动，我们将-90°弯管迎流而置。在同一流线上有m和n两点。m点的压力为p，速度为c；n点迎水而置，故其上的速度c_n=0，压力为p_n，故称n点为滞止点，p_n为滞止压力。由于Z_m=Z_n，则应用理想不可压缩的伯努利方程得

或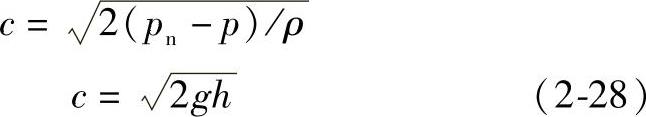

式中 gh——gh=（p_n-p）/ρ；

h——h=（h_n-h_m）为压力计测得之液柱差。(www.xing528.com)

考虑到实际气体有粘性，且弯管对流动也有影响，故用一系数ϕ修正之，则公式（2-28）可写成

上述弯管称皮托管，它可用于测量流体速度。有关皮托管的具体应用，将在试验装置中详细说明。一般ϕ≈1。

3.进气集流器测流量

图2-4为进气集流器。我们将伯努利方程应用于0-0和1-1截面上。0-0截面为大气，故其压力p₀=0（表压），且速度c₀≈0。故有

或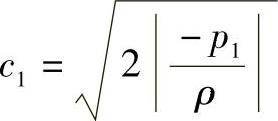

集流器流量为

式中，ϕ为流量系数，对圆弧形集流器ϕ=0.99，对锥形集流器ϕ=0.96，压力p₁为负值，计算上取其真空液柱高度h₁=|-p₁|。

图2-2 静力学例图

图2-3 皮托管原理简图

图2-4 进气集流器