混凝土生产系统的调度算法选择与实施

根据前面几节对调度子系统的分析,本系统的结构十分明确,生产工序和任务都是确定的。可能出现的各种故障状态也较为确定,因而本系统的行为可预测性较强。为了能够更好地分析整个混凝土的生产、运输和浇筑系统的性能,抽象出如下排队论模型。考虑到生产实际的需要,设计了较为合理的启发式算法。

(一)排队论模型

排队系统评价指标包括:系统中顾客的平均逗留人数Ls、系统中每个顾客的平均逗留时间Ws、队列中顾客的平均数(不包含正被服务的顾客)Lq、队列中每个顾客的平均等待时间(不包含正被服务的顾客)Wq、顾客到达不必等待的概率P0。

在系统平衡状态下,解得稳态概率

一般地,记状态上限为N,无限状态为N→∞;而对有限状态,则当n>N 时,Pn=0。

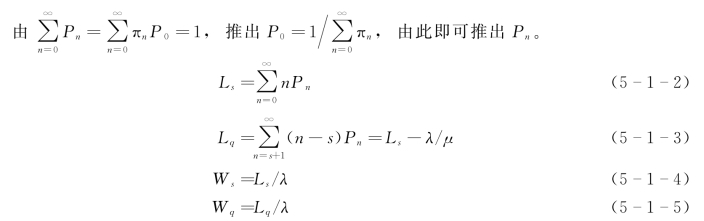
系统运行过程中,系统设备难免会发生故障,当系统发生严重故障时,系统按①与其他路线的任务争用设备;②按照原有确定设备配合关系运行。两种方案的平均等待时间分别为W 1 和W 2。

1.方案①

这种情况,系统的资源争用来自于不同浇筑设备的几个任务序列。例如,当由于某个搅拌罐出现重大故障必须停机检修时,该搅拌机中的任务就要和其他搅拌机中的任务争用设备,此时该系统为有优先权服务的排队系统。假定优先权分为N 级,第一级最优先,逐步次之;又设当若干具有同级优先权的顾客处于排队系统中,则按照先到先服务的原则。

优先级1为:因发生停机故障而不得不转移到别的设备上的任务;优先级2为:其他。

考虑任务输入时间间隔和服务时间都遵从负指数分布,其中所有不同优先等级的平均服务时间相等为μ,但第j优先等级的平均到达率为λj(j=1,2,…,N),K 为服务台数,记

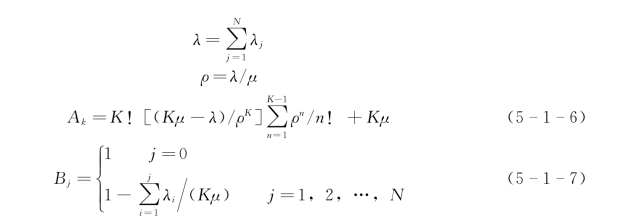
优先服务系统大致可分为两类:

(1)一般优先服务。当有优先权等级的顾客进入排队系统时,需等到正在得到服务的顾客完成后才能得到服务。

(2)紧急优先服务。当一个具有较高优先权的顾客进入排队系统时,正在得到服务的较低优先等级的顾客必须立即让位,重新排队等待。

根据混凝土生产的实际情况,一般不允许存在紧急优先服务,因为这样会造成大量废料,与尽量减少废料的要求相违背,所以考虑一般优先服务的情况。

经分析可得任一个有第j级优先权的顾客的服务质量。

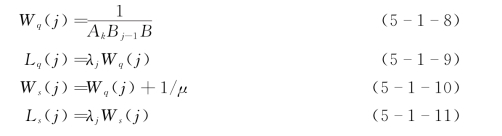
这样,平均等待时间为

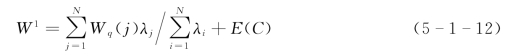
式中 E(C)——因争用设备而产生的设备转接时间的期望。2.方案②

这种情况,系统等价为4个M/M/1/FCFS 系统的并列,其中来自1号浇筑设备的任务到达服从参数为λ1 的负指数分布,来自2号浇筑设备的任务到达服从参数为λ2 的负指数分布,来自3号浇筑设备的任务到达服从参数为λ3 的负指数分布,来自4号浇筑设备的任务到达服从参数为λ4 的负指数分布,满足。

这样来自于各个不同浇筑设备的任务序列,分别在该浇筑设备对应的配套设备上面搅拌、运输和浇筑。这时任务对服务台的争用限于来自于同一浇筑设备的任务序列。

所以

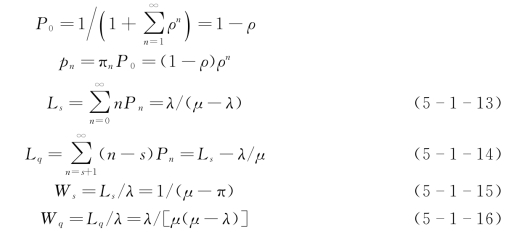
对应于4台浇筑设备的浇筑任务,有

综合上述,从平均等待时间最小原则出发,可得到最优方案。

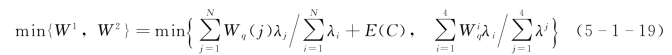
(二)启发式算法

在实际系统运行的正常情况下,参与混凝土生产、运输和浇筑的各个设备按照作业规划规定的作业配合关系和来料流程表运作。当有外部事件发生时(包括仓面调度发来的作业调整信息、设备停机故障等),调用调度策略进行实时调度。调度策略是一种算法,根据所搜集到的系统各个部分的实时状况,进行分析综合后按一定的规则向各个相关工作站发出控制信号,指挥系统协调运行。这个规则可以是一般的逻辑函数关系,也可以是一个专家系统或是两者的结合。

系统运行过程中可能出现的问题有很多,它们可能出现在任何时间和任何地点。例如,运输系统中的计量皮带或永久供料线的任何一个胶带机出现不能启动、不能定位、打滑、跑偏、堵料或急停故障等影响生产的情况时,都被认为是计量皮带或永久供料线故障。再如,生产出来的混凝土,出现温度过高、泛浆或搅拌不匀等现象,都属于质量不合格。在实际运行时,为了便于维修,要提示确切的故障位置。但不必对每一种情况都制订一种对策,因为很多种故障对系统造成的影响是相同的,可以将它们合并为一类故障,制订一个通用的对策加以处理。根据处理方法的不同,可将所有对策归纳为以下几类:

(1)某条生产线上只有一个搅拌机发生了故障。这时仍可以继续生产,但效率降低了。逻辑程序为:

IF 1号拌和楼的1号搅拌机故障OR 2号搅拌机故障THEN

IF 1号拌和楼的3号搅拌机故障OR 4号搅拌机故障THEN

IF 2号拌和楼的1号搅拌机故障OR 2号搅拌机故障THEN

IF 2号拌和楼的3号搅拌机故障OR 4号搅拌机故障THEN

提示故障报警

IF能够满足正常生产需要THEN(www.xing528.com)

IF故障搅拌罐中有任务THEN

将故障搅拌罐中的产品清除

将清除的任务加入待生产队列

IF在此任务之后另一个搅拌罐已有开始生产的任务THEN

将这个搅拌罐中的产品清除

将清除的任务加入待生产队列

END

END

ELSE

END

END

(2)某条生产线上的两个搅拌机、出料弧门或计量皮带等没有备份的环节发生了故障。这时不能继续生产,必须更换生产线(逻辑程序略)。

(3)生产出来的混凝土不合格,必须重新生产(逻辑程序略)。

(4)供料线出现故障(逻辑程序略)。

(5)出现不可克服的故障,只能停产(逻辑程序略)。

当外部事件发生,例如某一计量皮带发生急停故障时,不妨假设有如下3种调度策略可供选择:①等待修复;②改为汽车运输至仓位,采用港机或门机浇筑;③切换至其他拌和楼,采用其他塔式布料机协助浇筑。

仿真以上3种调度策略,得到最佳决策①或②或③,以使总费用最小,这里的费用概念涵义很广,既可包括因等待而造成的生产损失,又可包括因延误生产而造成的废料损失等。

这相当于一个决策问题,包括一定的目标、决策者、可供决策者选择的可能行动(策略和方案)和采取这些可能行动后所造成的所有可能结果,决策过程就是从可能达到一定目标的一系列可能行动、策略和方案中选出一个特定的行动,以得到最好的结果。决策过程是一个复杂的判断过程,需要对客观事物的本质有足够的了解,收集信息,分析处理,最后由决策者做出正确的选择。

一般而言,决策有状态、策略和收益3个要素。

考虑策略①等待修复。这时面对的状态可能为:

状态a,在允许时间内修好,概率为P1,费用包括等待费用;

状态b,在允许时间内不能修好,概率P2,费用包括因延误造成的废料费用。

式中 f i——对各项费用的估计函数,这些函数由相应统计资料拟合而成。

考虑策略②改为汽车运输至仓位,采用港机或门机浇筑。费用包括速度损失费用、等待费用等。

考虑策略③切换至其他拌和楼,采用其他塔式布料机协助浇筑。费用包括设备切换费用、等待塔式布料机空闲费用等。同理可得到E[T2]、E[T3]。

若采用策略③,则上述过程还需确定一台最适合分配的拌和楼。这可以看作是从N个任选项中确定一个解答的问题。这里的N 是系统拌和楼中的搅拌罐数。

通过计算一个设定的函数J(i)来评价分配哪一台拌和楼的哪一个搅拌罐最合适。评价函数J(i)根据预测运算的结果来确定,各个拌和楼的评价公式如下

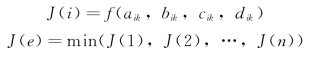
式中 e——被分配的搅拌罐;

J(i)——评价函数;

aik——各个搅拌罐的平均服务时间;

bik——各个搅拌罐的故障概率;

cik——各个搅拌罐的预测完工时间;

dik——预计修复时间。

评价公式中还可以加入转换时间等其他性能标准。一般将J(i)示为各个性能标准的加权和形式,即

式中 pi——加权系数,i=a、b、c、d,且∑pi=1;

wi(i=a,b,c,d)——对aik、bik、cik、dik的估计函数或预测函数。

在开发中,将不同的调度策略实现为不同的调度成员函数,供系统中的对象实体调用。这些成员函数还可以传入不同的参数,以考察同一类策略在不同参数情况下的性能。