脉冲分压电路的工作原理与应用

利用两个电阻串联可以组成普通的电阻分压器，如图5-21所示。

当t=0时刻，电路中输入一幅度为E的阶跃信号，在R₂两端可以得到u_o=ER₂/（R₁+R₂）的输出。然而在实际电路中经常存在由元件引线并行排列引起的如图5-21所示虚线部分表示的分布电容C₀，它的存在会使输出波形发生改变，引起失真，如图5-22所示。

分析有分布电容C₀存在时电阻分压电路的工作情况。由于C₀是并联在电阻R₂上的，当输入一个矩形脉冲信号时，输出u_o=u_C不能相应产生突变，只能随着C₀的充电过程按指数规律逐渐升高。u_o经过了3～5τ的时间[τ=C₀R₁R₂/（R₁+R₂），是电路时间常数]后趋于稳态。u_o的最大值为R₁、R₂分压得到的输出值E_R，如图5-22b所示。其中，虚线部分是不考虑C_o影响时的理想波形与图5-22a所示的输入波形对应，实线部分是考虑C_o影响时的波形。一般C_o的数值在几皮法至几十皮法之间，相应τ值较小。当输入矩形波信号工作频率较低时，影响不明显。但当信号工作频率较高时，需要考虑克服波形改变引起的失真。

为了消除C_o的影响，可以采用图5-23所示的RC分压电路。

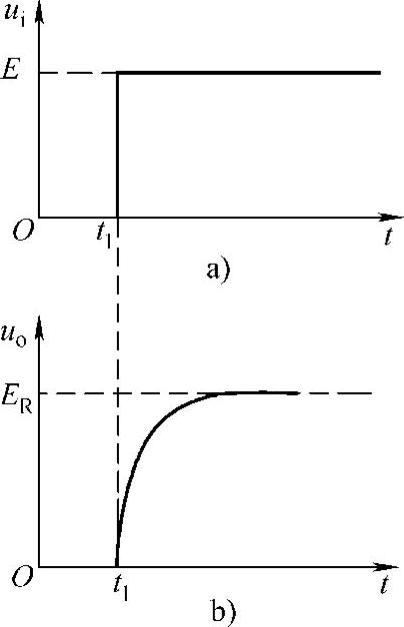
图5-22 考虑分布电容影响的波形

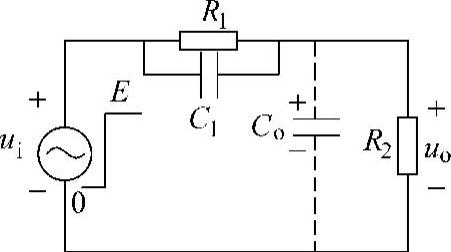
图5-23 RC分压电路

此电路与普通电阻分压器的区别在于输入电阻R₁上并联了一个电容C₁。从电路结构可以看出，C₁和C_o串联，输出来自它们的连接点。

电容的特性是隔直流、通交流，遇到直流电时，电容相当于断路。电容对于交流信号有与电阻类似的阻碍作用，称为容抗，其大小与交流信号的频率成反比、与电容的电容量成反比。若不考虑相位的变化，电容C的容抗Z_C可写为

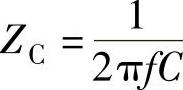
对于交流信号，电容串联也有分压作用，分压值的计算方法同电阻分压的计算一样。当输入信号发生从0到E跳变时，由频谱分析可知，该瞬间相当于把一个频率很高的信号加到电路的输入端。电容对高频率交流信号的容抗远小于电阻的阻抗，电阻的作用可以忽略不计。也就是说在t=0时，输入发生从0到E的正跳变瞬间，输出u_o（0）的大小近似由两个电容的分压比决定：

u_o=EZ_o/（Z₁+Z_o）=EC₁/（C₁+C_o）式中，Z₁和Z_o分别为C₁和C_o的交流阻抗。经过3～5τ的时间后，电容的充电过程基本结束，Z₁→∞，Z₀→∞，u_o基本稳定在由R₁和R₂分压得到的输出值：

u_o=ER₂/（R₁+R₂）式中，τ为图5-23所示RC分压电路的时间常数，即

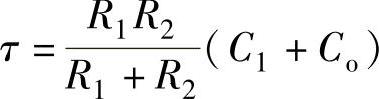(www.xing528.com)

电容分压比和电阻分压比不同时，输出波形会有不同的变化。令

N_C=C₁/（C₁+C_o），N_R=R₂/（R₁+R₂）

E_C=EN_C，E_R=EN_R

分以下三种情况讨论：

①N_C<N_R：t=0时，输出u_o跳变到E_C<E_R，未达到稳定值，尚需经过3～5τ的时间，按指数规律变化的信号电压才达到稳定值u_o=E_R，如图5-24a所示。

②N_C>N_R：t=0时，输出u_o跳变到E_C>E_R，超过稳定值，经过一段时间按指数规律衰减到稳定值，如图5-24b所示。

③N_C=N_R：t=0时，输出u_o跳变到E_C=E_R，开始就达到稳定值，是最理想的情况，如图5-24c所示，分压波形可用示波器检测显示。

综上所述，只要适当选取C₁，使得N_C=N_R，可以使u_o开始就跳变到稳定值而不发生失真。C₁的接入使得输出波形前沿加速上升，故有时将C₁称为加速电容。

实际应用中，由于分布电容C₀的不确定性，使得C₁选取困难。这时可以在输出端（R₂两端）并联一个电容C₂，当C₂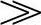C₀时，不确定因素引起的C₀变化的影响可以忽略。由C₂、R₁、R₂可以求得C₁、C₂，一般在几十皮法到几百皮法。

C₁=R₂C₂/R₁

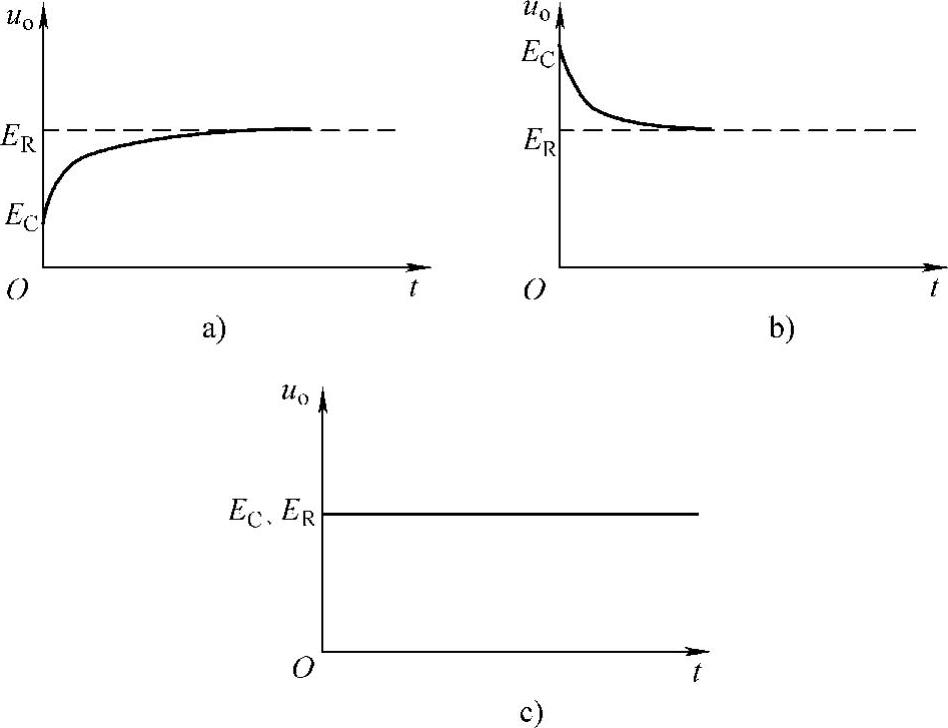
图5-24 RC分压电路输出波形

a）E_C＜E_R b）E_C＞E_R c）E_C=E_R