英国数学家乔治·布尔(George Boole)在19世纪中叶提出的逻辑代数理论为数字电路和20世纪最伟大的科技发明——计算机——奠定了理论基础。逻辑代数是用二进制代码表示事物二相性因果关系及信号的组合、变换规律的数学方法。对这些因果关系及其组合、变换规律的数学表述称为逻辑运算。
在客观事物的逻辑关系中,事件与条件之间有各种的制约关系。对照数学习惯,可以把客观事物之间的逻辑关系转换为抽象的逻辑运算,事件的条件是逻辑运算的自变量(简称变量),事件的状态是逻辑运算的结果,是逻辑变量的函数。所以,一个确定的逻辑运算关系又叫做一个逻辑函数。
把客观事物的两种相对立的状态用二进制代码表示称为逻辑赋值(简称为赋值)。在赋值时,通常把所关注的事物状态用1表示,把事物的另一种状态则用0表示。不同的赋值方式会得出不同的逻辑形式。也就是说,对于同一个事件,选用不同的赋值方式会表现出不同的逻辑关系。
1.基本逻辑
最基本的逻辑运算有与逻辑、或逻辑、非逻辑(又叫取反)三种。
(1)非逻辑(取反)及其表述。一个事件与它的条件如果是相互否定关系,它们的因果关系称为非逻辑。
例如,设备正常运行状态和故障状态的关系就是属于非逻辑,设备正常运行就不能有故障,有故障的设备不能正常运行。
设备和故障之间的状态表见表4-1。
若把设备的状态用S表示,能正常运行的状态赋值为1、不能正常运行赋值为0;故障用G表示,有故障赋值为1、没故障赋值为0,状态表即可转换为非逻辑真值表(见表4-2)。
在变量字母上方加一个横杠表示对这个变量进行非逻辑(也叫取反)运算。“-”号是非逻辑的运算符(又叫反号)。表4-2真值表表示的非逻辑写成表达式为
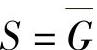
表4-1 设备和故障之间的状态表
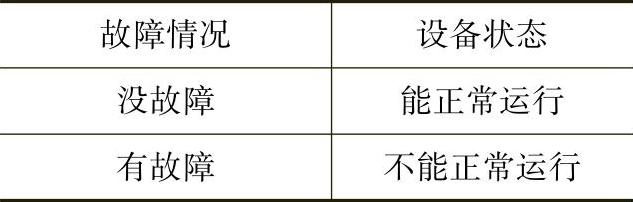
表4-2 非逻辑真值表
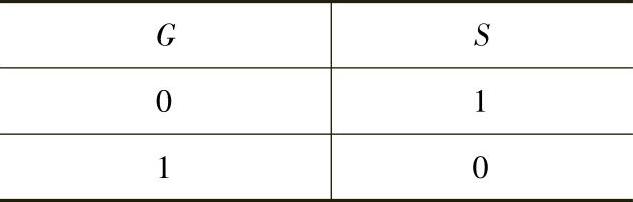
上述表达式可有“S等于G非”、“S等于G的非”、“S等于非G”、“S等于G反”、“S等于G的反”等多种读法。
非逻辑中的事物和条件是相互否定的关系,所以,上述关系也可表示为
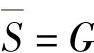
非逻辑的运算法则是:
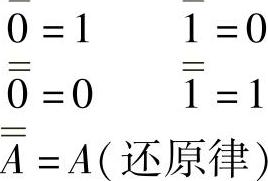
常见的非逻辑运算符的图形符号有三种,如图4-1所示。其中,图4-1a为国标符号,图4-1b为我国曾用过的符号,图4-1c为国外资料中常用的符号。

图4-1 常见的三种非逻辑符号
a)国标非逻辑符号 b)曾用非逻辑符号 c)国外资料中常用的非逻辑符号
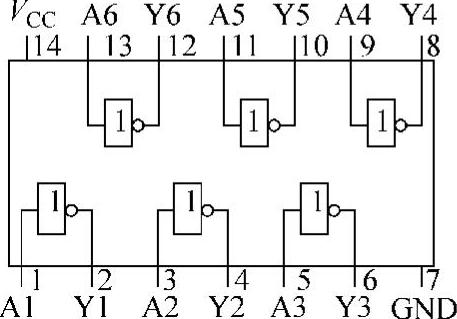
图4-27 404内部结构和外部引脚信号
7404是74系列中将6个非门(反相器)封装在一起的数字集成电路产品,其内部结构和外部引脚信号如图4-2所示。
选用7404芯片中的1个非门,输入端接逻辑输入开关,输出端接逻辑电平显示器(或用万用表的10V直流电压挡监测),再给电路接通电源,如图4-3a所示。按表4-2(非门逻辑真值表)变换非门的输入电平,就可以检测TTL非门的逻辑功能,画出电压波形,如图4-3b所示。
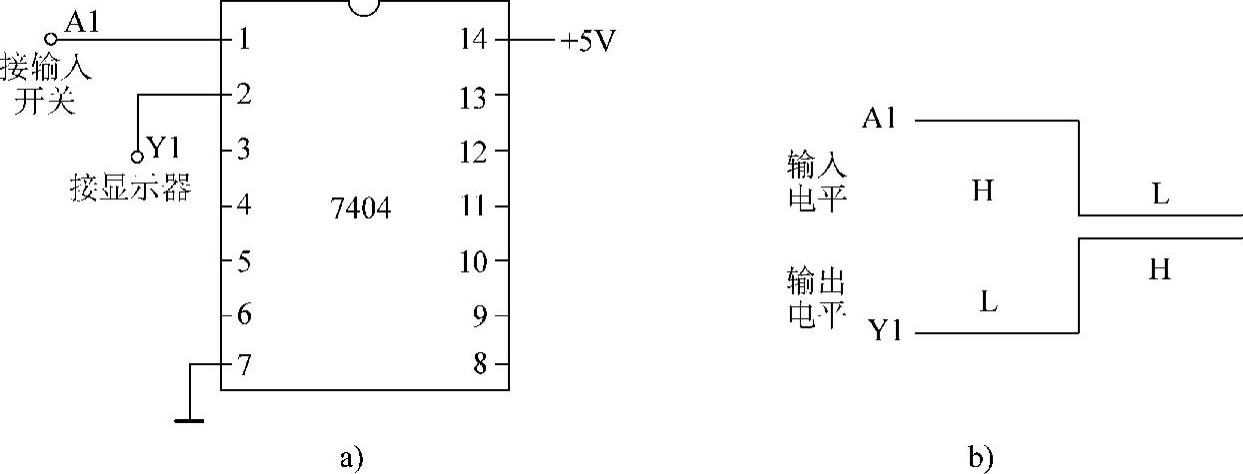
图4-3 利用7404测试非门逻辑功能
a)接线图 b)电压波形
若用两个非门串接,就可以验证还原律: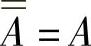 。
。
(2)与逻辑及其表述。事件由两个以上(含两个)的条件决定,并且只有全部条件同时具备时事件才能成立。这样的因果关系称为与逻辑关系。
例如,防盗门有两道锁,只有两道锁都打开时,门才能打开,门的打开状态与两个锁打开的因果关系就属于与逻辑关系。
假设,防盗门的两道锁用A、B表示,门用M表示,门和两个锁的全部状态的对应关系可列成一个表,叫做状态表,见表4-3。两把锁A、B的状态组合共有4种(二相性事物的状态组合总数为2N,N为事物数量)。
表4-3 门和锁的关系状态表
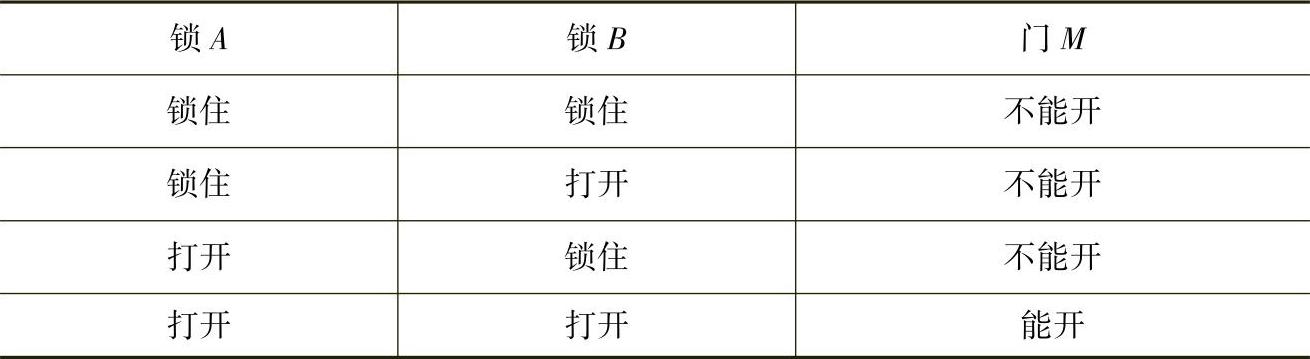
按题目的关注点,把锁的打开状态和门的能开状态都用1表示;锁的锁住状态和门的不能打开状态用0表示。赋值后,状态表就转换为真值表,见表4-4。真值表中逻辑变量A、B的取值组合与状态表中相对应,总数也是2N,N是变量的个数。
表4-4 门和锁的关系真值表

这种输入变量取值有0,输出函数值就为0;只有变量值全为1时,函数值才为1(即:有0即0,全1为1)的特性就是与逻辑的函数规律。
这种逻辑函数关系用表达式表示:
M=A·B
表达式中“·”是与逻辑的运算符,与运算符可省略不写,表达式写成:
M=AB
在不能省略又不便用“·”表示时也可用“∧”号表示,写成:
M=A∧B
与逻辑又可叫做“逻辑与”、“逻辑乘”,表达式读作“M等于A与B”或“M等于A乘B”。
与逻辑的运算法则是:
① 数值运算:(这里的与运算符既不能省略,又不宜用·表示)
0∧0=0
0∧1=1∧0=0
1∧1=1
② 变量运算:
AB=BA(交换律)
ABC=(AB)C=A(BC)(结合律)
AA=A(重叠律)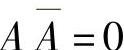
(互补律)
③ 变量和数值的运算:
A·1=A
A·0=0
对于表4-2中的逻辑函数关系的理解可用表4-5加以说明。
表4-5 与逻辑关系真值表的说明

常见的与逻辑运算符的图形符号(通常叫做与逻辑符号)有三种,如图4-4所示后两种符号读者在旧教材、旧技术资料或引进的技术资料中会遇到,本书也有使用。下文内容中还有这样的情况,不再重复。
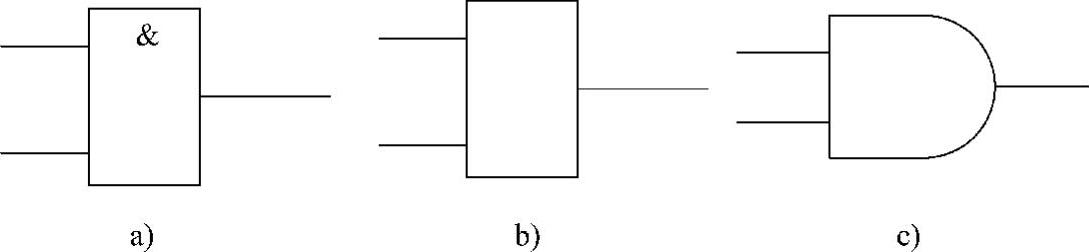
图4-4 常见的三种与逻辑符号
a)国标与逻辑符号 b)曾用与逻辑符号 c)国外资料中常用的与逻辑符号
逻辑符号是一种图形化的逻辑运算符,具有双重含义,它既表示一种逻辑运算,又表示能实现该种逻辑运算功能的逻辑门电路。
7408是74系列芯片中有4个二输入端与门的数字集成电路产品,其内部结构和外部引脚信号如图4-5所示。
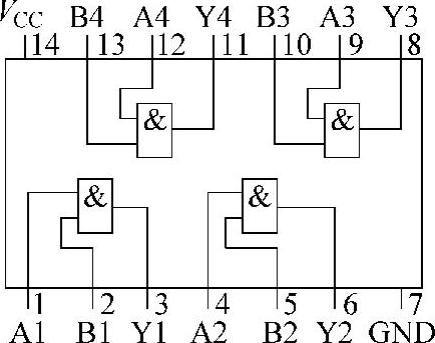
图4-57 408内部结构和外部引脚信号
用7408检测与门的逻辑功能时,选用7408数字芯片中的1个与门,给与门的两个输入端各接一个逻辑输入开关,输出端接逻辑电平显示器(或用万用表的10V直流电压挡监测),再给电路接通电源,如图4-6a所示。按表4-4(与逻辑真值表)变换输入电平的组合状态,就可以检测TTL与门的逻辑功能,画出电压波形,如图4-6b所示。
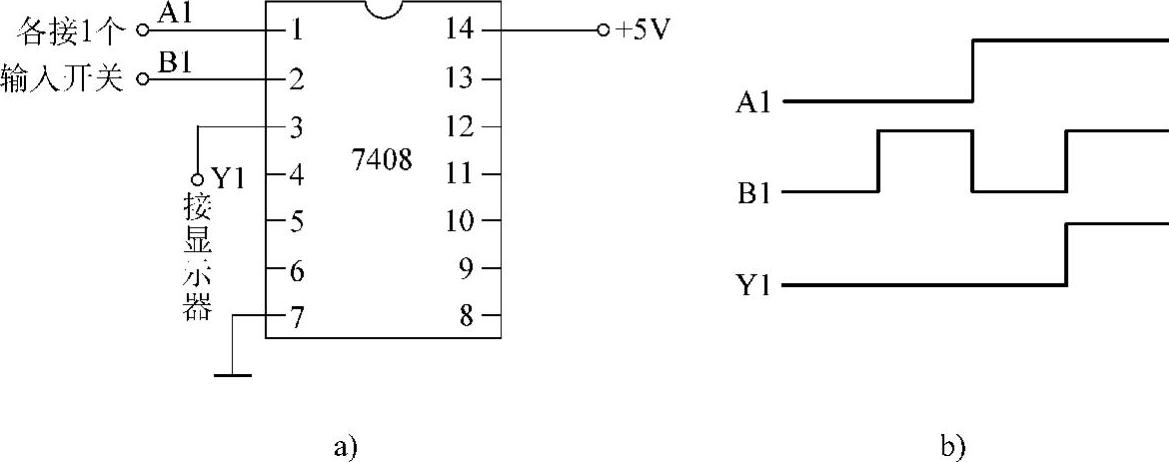
图4-6 利用7408测试与门逻辑功能
a)接线图 b)电压波形
(3)或逻辑及其表述。一个事件由两个以上(含两个)的条件决定,并且是只要有一个条件具备事件就能成立。这样的因果关系称为或逻辑关系。
若把上例中防盗门的不能开状态跟两道锁的锁住状态作为关注的因果关系,那么它们就是或逻辑关系。
把表4-3中关注的门不能开和两道锁的锁住状态用1表示,打开两个锁和开门状态用0表示,则得到或逻辑的真值表(见表4-6),表4-7是或逻辑的真值表的习惯表示方式。
表4-6 或逻辑的真值表
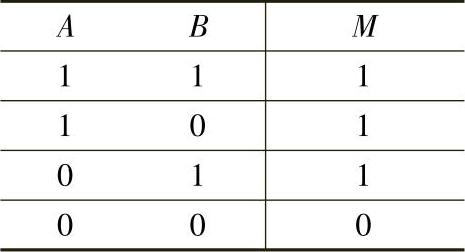
表4-7 或逻辑的真值表的习惯表示方式
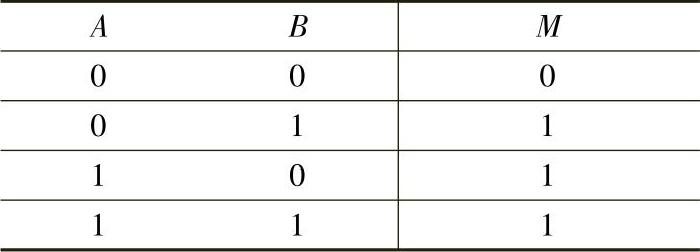
这种输入变量取值有1时,输出函数值就为1;只有变量值全为0时,函数值才为0(即:有1为1,全0为0)的特性就是或逻辑的函数规律。
这种逻辑函数关系用表达式表示:
M=A+B
表达式中“+”是或逻辑的运算符,或运算符不可省略,当或运算跟算术加法“+”共同存在时可用“∨”符号,写成:
M=A∨B
或逻辑又可叫作“逻辑或”、“逻辑加”,表达式读作“M等于A或B”或“M等于A加B”。
或逻辑的运算法则是:
① 数值运算:
0+0=0
0+1=1+0=1
1+1=1
② 变量运算:
A+B=B+A(交换律)
A+B+C=(A+B)+C=A+(B+C)(结合律)
A+A=A(重叠律)
A+A=1(互补律)
③ 变量和数值的运算:
A+1=1
A+0=A
对于表4-5中的逻辑函数关系的理解可用表4-8加以说明。
表4-8 或逻辑真值表的说明

常见的或逻辑运算符的图形符号有三种,如图4-7所示。
7432是74系列芯片中有4个2输入端或门的数字集成电路产品,其内部结构和外部引脚信号如图4-8所示。
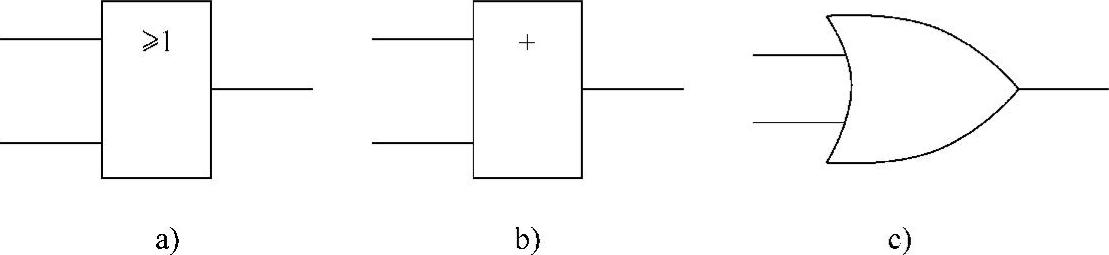
图4-7 常见的三种或逻辑符号
a)国标或逻辑符号 b)曾用或逻辑符号 c)国外资料中常用的或逻辑符号
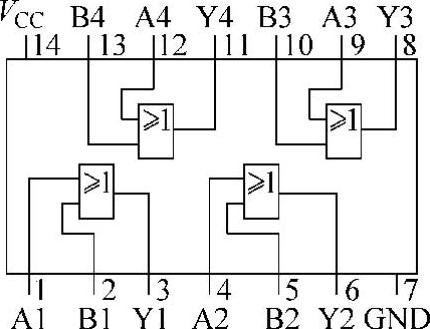
图4-8 7432内部结构和外部引脚信号
用7432检测或门的逻辑功能时,选用7432芯片中的1个或门,给或门的两个输入端各接一个逻辑输入开关,输出端接逻辑电平显示器(或用万用表的10V直流电压挡监测),再给电路接通电源,如图4-9a所示。按表4-7(或逻辑真值表)变换输入电平的组合状态,就可以检测TTL或门的逻辑功能,画出电压波形,如图4-9b所示。
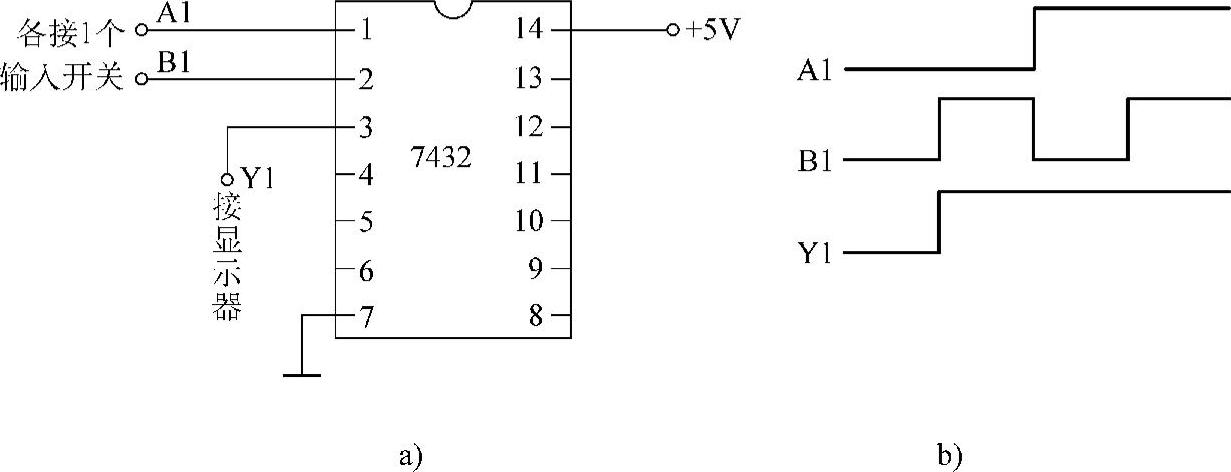
图4-9 利用7432测试或门逻辑功能
a)接线图 b)电压波形
三种基本逻辑运算的运算顺序是:在同等情况下,先做非运算、后做与运算、再做或运算,对于超越运算顺序的部分要加括号(非号对于它覆盖的逻辑运算相当括号作用,运算由内向外逐层执行)。
例如表达式:
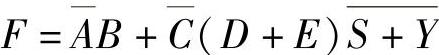
式中,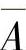 、
、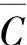 表示的求反运算是第一层运算,(D+E)、
表示的求反运算是第一层运算,(D+E)、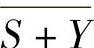 中的或运算是第二层运算,
中的或运算是第二层运算,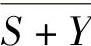 或运算结果求反是第三层运算,第四层是
或运算结果求反是第三层运算,第四层是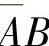 、
、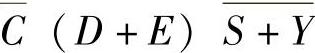 两组与运算,最后是两组与运算结果的或运算,也是整个表达式的运算结果。
两组与运算,最后是两组与运算结果的或运算,也是整个表达式的运算结果。
2.重要的复合逻辑
除三种基本逻辑以外,还有几种复合逻辑同样是非常重要的,成品的逻辑电路芯片中也有对应的产品。
(1)与非逻辑。与非逻辑是与逻辑和非逻辑的复合,有相应的逻辑符号予以表示,如图4-10所示。(https://www.xing528.com)
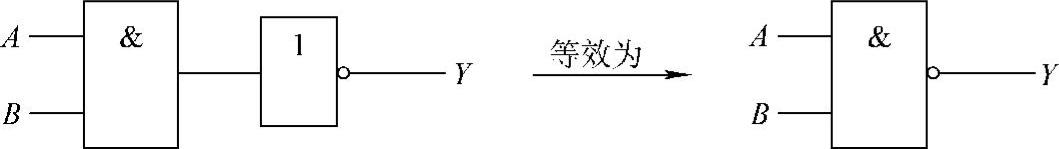
图4-10 与非逻辑的复合和其组合逻辑符号
图4-10所示的与非逻辑其表达式为
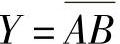
表达式中的反号应覆盖作与运算的A、B两个字母,表示对A、B两个变量的与运算结果取反,而不是对A、B两个变量取反,所以,运算时要由内向外、先与后非。
表4-9是与非逻辑的真值表,为便于读者理解,表中附加了A、B相与的中间结果。
表4-9 与非逻辑的真值表
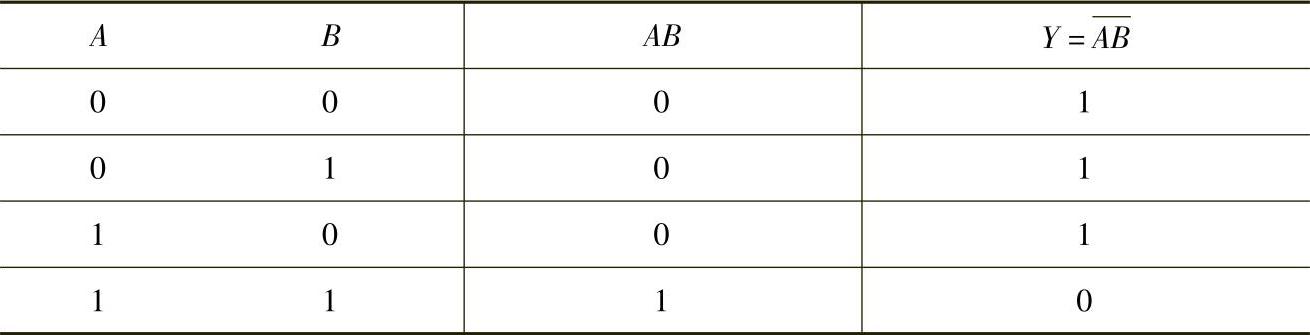
对于与非逻辑的输入、输出之间的取值规律可总结为:有0为1,全1为0。
7400是74系列芯片中有4个2输入端与非门的数字集成电路产品,其内部结构和外部引脚信号如图4-11所示。
用7400检测与非门的逻辑功能时,选用7400数字芯片中的1个与非门,给与非门的两个输入端各接一个逻辑输入开关,输出端接逻辑电平显示器(或用万用表的10V直流电压挡监测),再给电路接通电源,如图4-12a所示。按表4-9(与非逻辑真值表)变换输入电平的组合状态,就可以检测TTL与非门的逻辑功能,画出电压波形,如图4-12b所示。
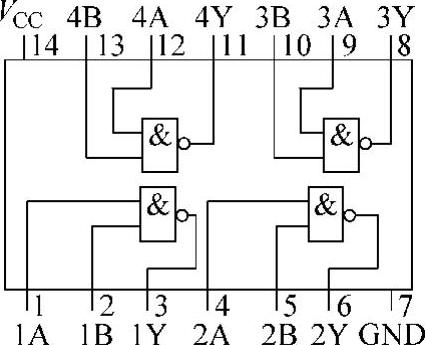
图4-11 7400内部结构和外部引脚信号
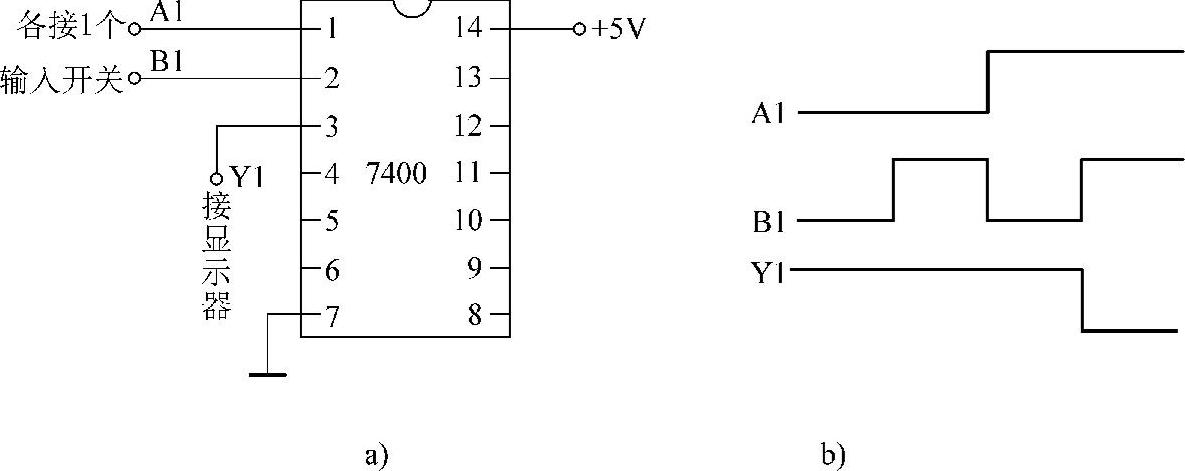
图4-12 利用7408测试与非门逻辑功能
a)接线图 b)电压波形
(2)或非逻辑。或非逻辑是或逻辑和非逻辑的复合,有相应的逻辑符号予以表示,如图4-13所示。
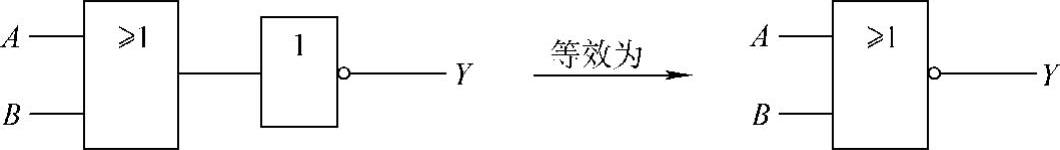
图4-13 或非逻辑的复合及其组合逻辑符号
图4-13所示的或非逻辑其表达式为
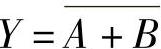
表达式中的非号要覆盖整个参与或运算的内容,表示对A、B两个变量的或运算结果取反。运算时要由内向外、先或后非。
或非逻辑的真值表见表4-10(表中附加有A、B相或的中间结果)。
表4-10 或非逻辑的真值表

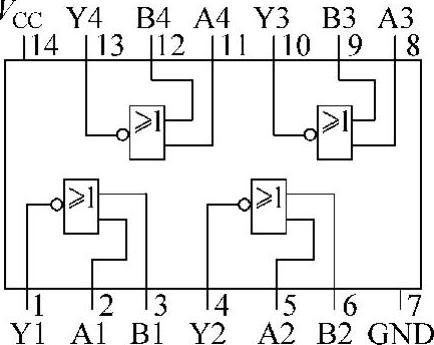
图4-14 7402内部结构和外部引脚信号
对于或非逻辑的输入、输出之间的取值规律可总结为:有1为0、全0为1。
7402是74系列中的4个2输入端或非门封装在一起的数字集成电路产品,其内部结构和外部引脚信号如图4-14所示。
用7402检测或非门的逻辑功能时,选用7402数字芯片中的1个或非门,给或非门的两个输入端各接一个逻辑输入开关,输出端接逻辑电平显示器(或用万用表的10V直流电压挡监测),再给电路接通电源,如图4-15a所示。按表4-10(或非逻辑真值表)变换输入电平的组合状态,就可以检测TTL或非门的逻辑功能,画出电压波形,如图4-15b所示。
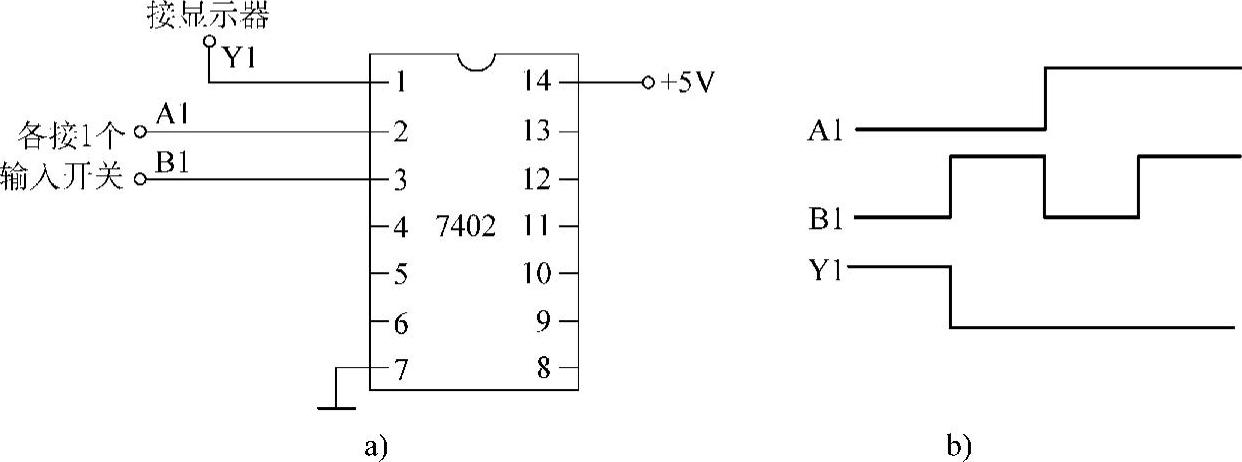
图4-15 利用7402测试或非门逻辑功能
a)接线图 b)电压波形
(3)与或非逻辑。与或非逻辑是与逻辑、或逻辑和非逻辑的三种运算复合,也有相应的逻辑符号予以表示,如图4-16所示。
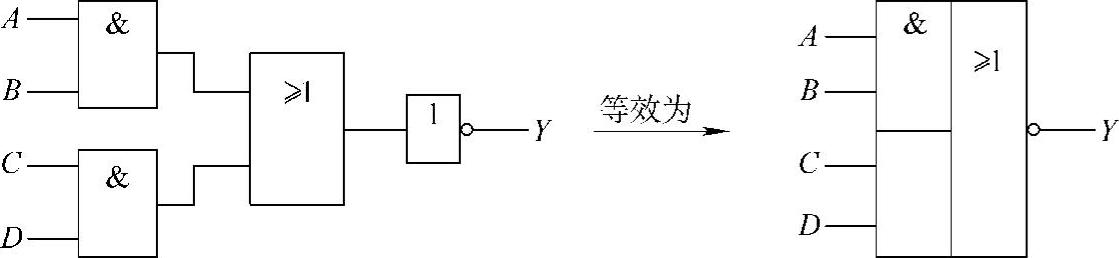
图4-16 与或非逻辑的复合及其组合逻辑符号
图4-16所示的与或非逻辑其表达式为
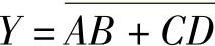
表达式中的非号要覆盖整个与或运算的全部内容,表示对与、或运算的最后结果取反。
表4-11是与或非逻辑的真值表。
表4-11 与或非逻辑的真值表
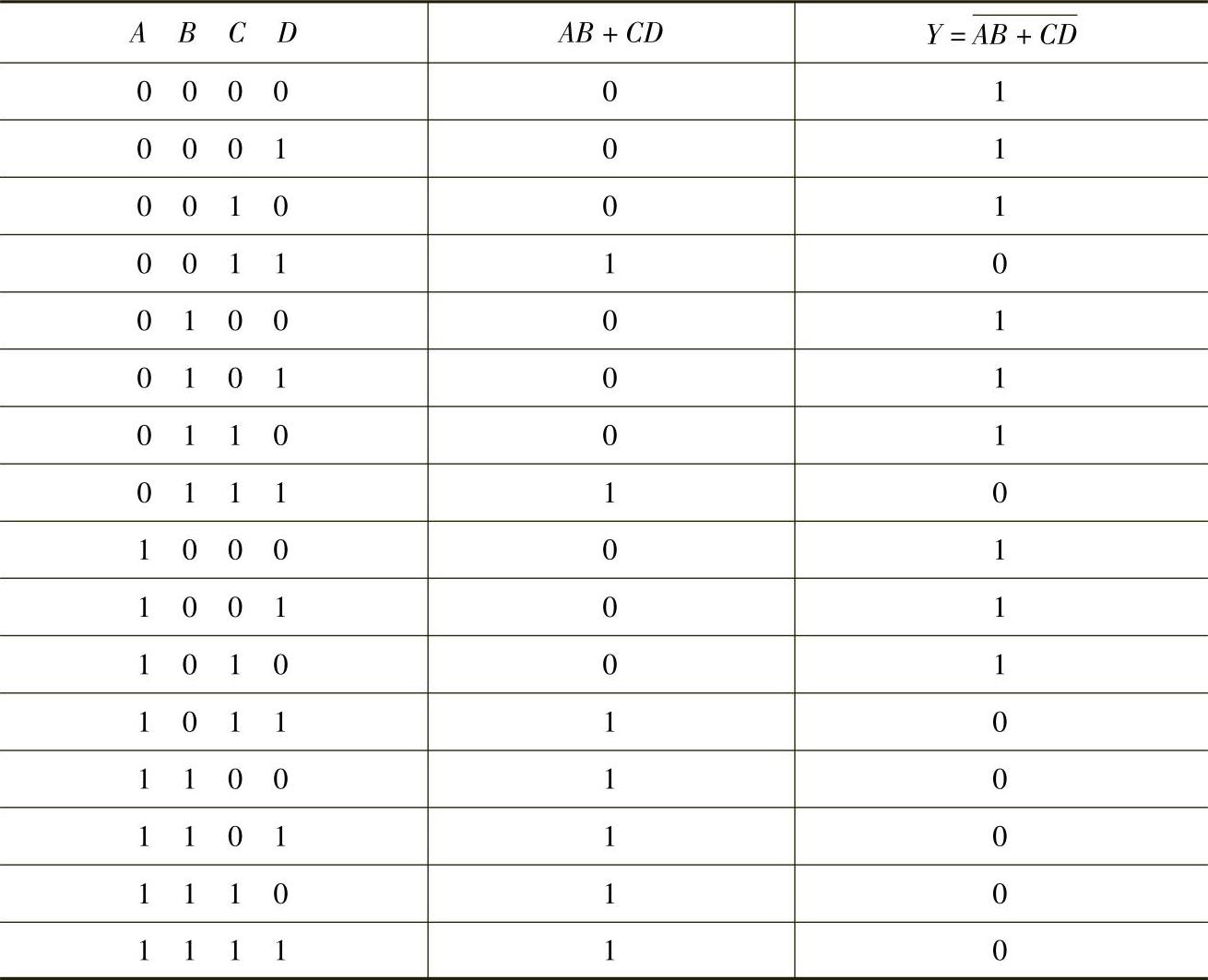
函数有A、B、C、D四个变量,变量取值组合总数为0000~1111,共16(也就是24)种。
7451是74系列芯片中有双与或非门数字集成电路产品,其内部结构和外部引脚信号如图4-17所示。
用7451检测与或非门的逻辑功能时,给与或非门的4个输入端各接一个逻辑输入开关,输出端接逻辑电平显示器(或用万用表的10V直流电压挡监测),再给电路接通电源,如图4-18a所示。按表4-11(与或非逻辑真值表)变换输入电平的组合状态,就可以检测TTL与或非门的逻辑功能,画出电压波形,如图4-18b所示。
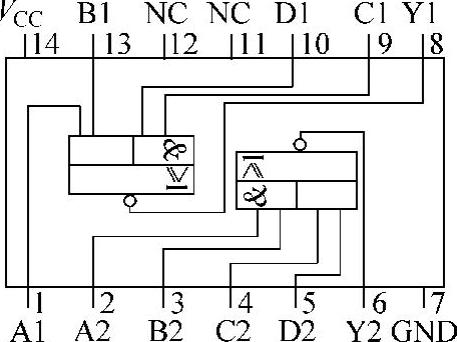
图4-17 7451内部结构和外部引脚信号
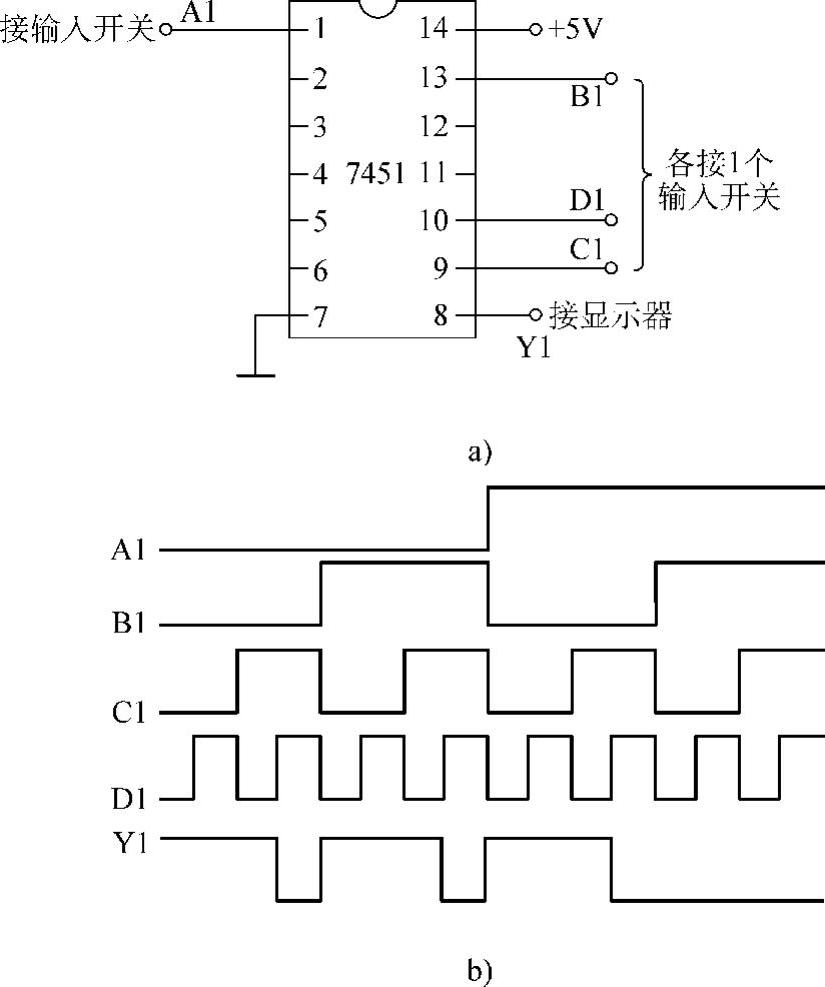
图4-18 利用7451测试与或非门逻辑功能
a)接线图 b)电压波形
(4)异或逻辑。异或逻辑是一种重要的复合逻辑,它表示一个事件由两个条件决定,当两个条件不同时具备时,事件才能成立;而两个条件同时具备或同时,不具备时事件不能成立。异或逻辑的复合关系及逻辑符号,如图4-19所示。
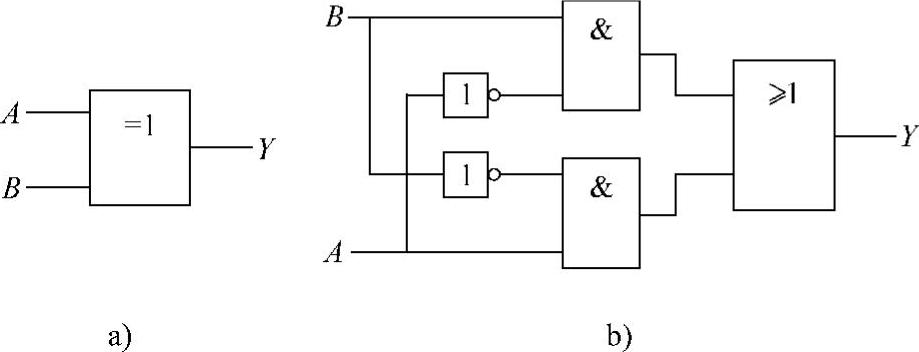
图4-19 异或逻辑的复合关系及其逻辑符号
a)异或逻辑符号 b)异或逻辑的等效复合关系
图4-19所示的异或逻辑及其复合关系的表达式为
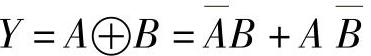
根据异或逻辑的等效复合关系,“异或”一词可以直观的理解为两个逻辑变量的“异”状态相与、再“或”的结果。表达式中的“⊕”为异或运算符。
异或运算法则是:
① 数值运算:
0⊕0=1⊕1=0
0⊕1=1⊕0=1
② 变量运算:
A⊕B=B⊕A(交换律)
A⊕B⊕C=(A⊕B)C=A(B⊕C)(结合律)
A⊕A=0(重叠律) (互补律)
(互补律)
③ 变量和数值的运算:
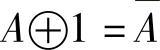
A⊕0=A
表4-12是异或逻辑的真值表。
表4-12 异或逻辑的真值表
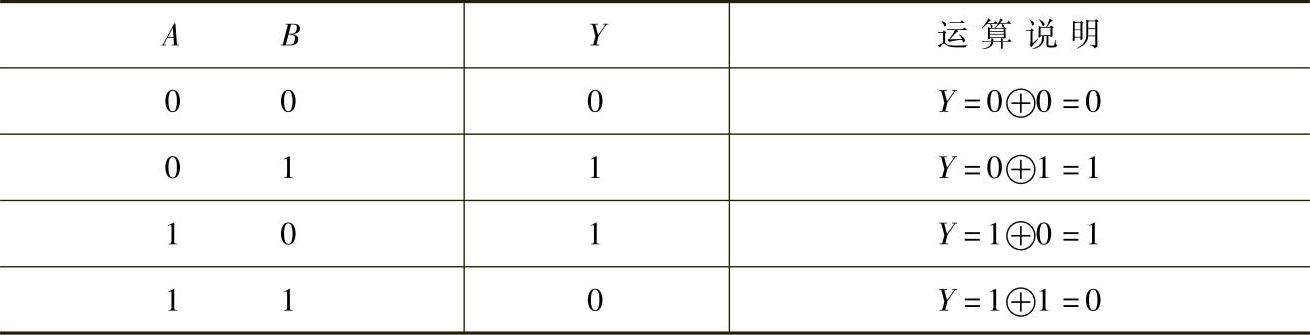
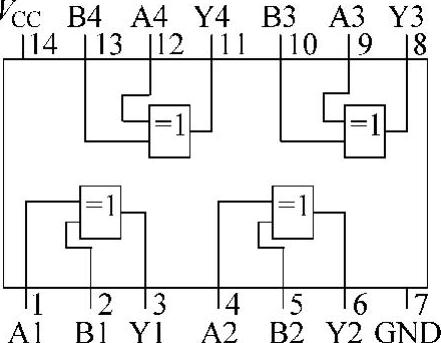
图4-20 7486内部结构和外部引脚信号
异或逻辑运算规律可归纳为:同为0,异为1。
7486是74系列芯片中有4个2输入异或门的数字集成电路产品,其内部结构和外部引脚信号如图4-20所示。
用7486检测异或门的逻辑功能时,选用7486中的一个异或门,给异或门的两个输入端各接一个逻辑输入开关,输出端接逻辑电平显示器(或用万用表的10V直流电压挡监测),再给电路接通电源,如图4-21a所示。按表4-12(异或逻辑真值表)变换输入电平的组合状态,就可以检测TTL异或门的逻辑功能,画出电压波形,如图4-21b所示。
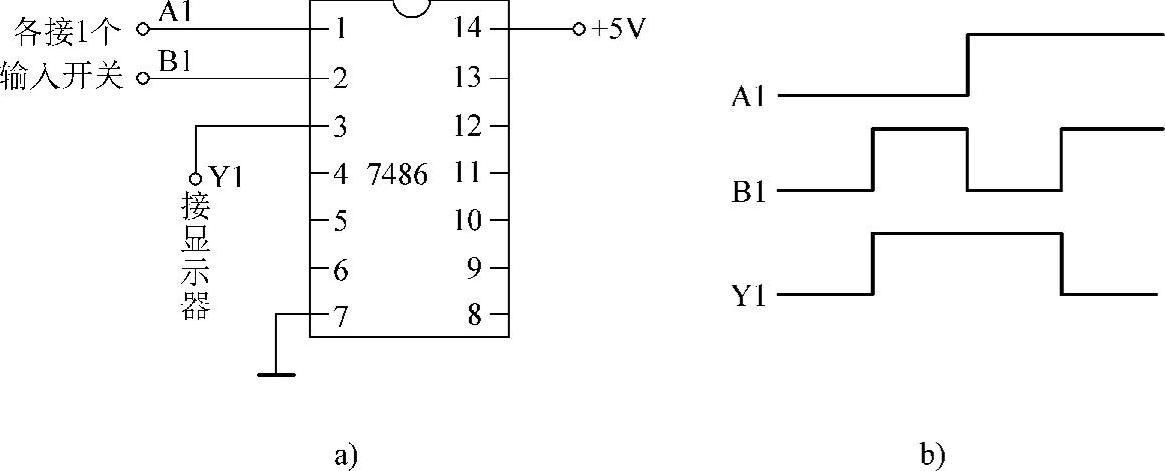
图4-21 利用7486测试异或门逻辑功能
a)接线图 b)电压波形
3.逻辑运算的重要法则和定律
逻辑代数是具有独立理论结构的复杂体系,支撑数字电路的只是其中最基础的部分。下面介绍的是处理逻辑电路时经常用到的几个法则和定律。
(1)逻辑表达式中的括号变换法则。括号变换法则:逻辑运算中对于括号的处理法则与普通数学一样,有加括号和去括号(也叫展开)两种互逆变换,展开括号运算如:
A(B+C)=AB+AC在逻辑代数中称之为“与对或的分配律”。
与展开括号相反,在提取公因子时,要加括号,如:
AB+AC=A(B+C)
这两个表达式在普通数学中已有定论,在逻辑代数中是否成立还须证明。在逻辑代数中,最基本的证明手段是真值表(一般情况可用已知定律证明)。对应变量的全部组合,如果两个函数的运算值完全相同,就证明这两个函数表达式相等。下面用真值表(见表4-13)证明它们成立。
表4-13 证明等式的真值表
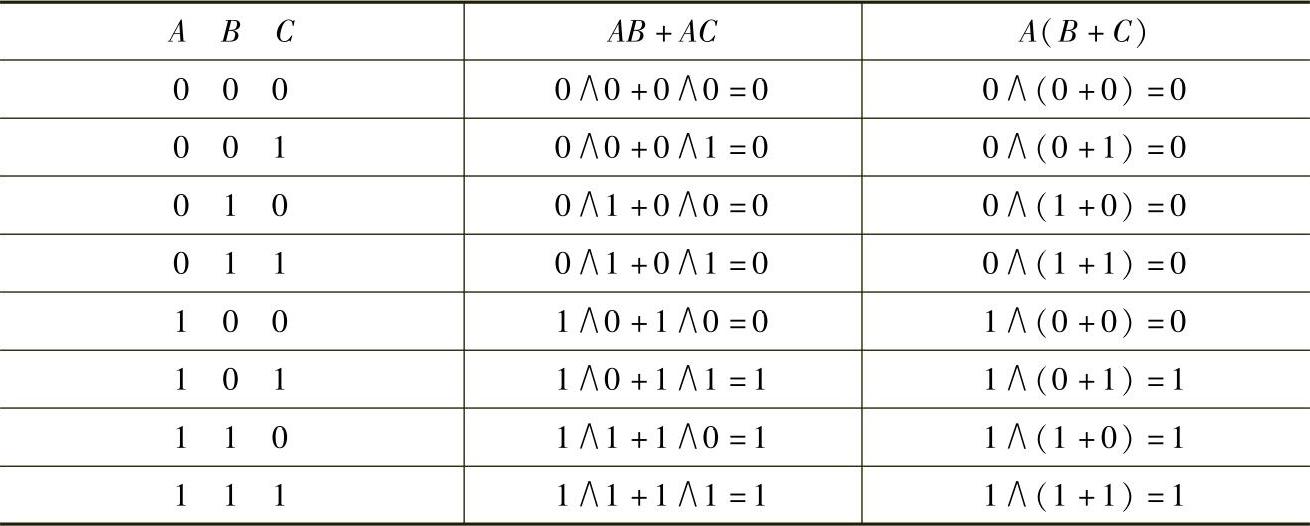
通过真值表的证明
AB+AC=A(B+C)
(2)逻辑表达式中的代入法则。代入法则:在逻辑运算中,任何变量都可以视作一个函数,而在逻辑函数表达式中,任何一个运算单元都可以用一个变量代换。如:
Y=AB+CD
若式中
D=MN+L
则有
Y=AB+C(MN+L)
如果又设
F=AB
表达式可变换为
Y=F+C(MN+L)
代入法则对理解和应用其他定律、法则有着重要意义,希望读者对此给予必要的重视。
(3)摩根定律及其应用表达式变换的意义。摩根定律是说明表达式中的与、或运算变换和反号的变换关系的定律,可以随时用于表达式任何部位的与、或运算变换,是表达式变换操作中的重要处理手段。
两个变量的摩根定律变换形式:
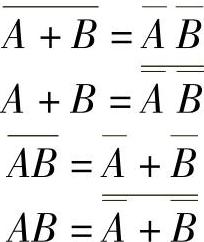
三个变量的摩根定律变换形式:
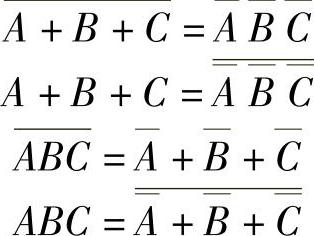
表达式中的各种逻辑运算是和逻辑门电路相对应的。摩根定律的变换式(还有其他的表达式变换)说明一个逻辑关系可对应多种表达式形式,也就是可用多种逻辑电路实现。这就为制作实际数字电路提供了充分的选择余地,也为识别实际数字电路提供了多种变换手段。因此,掌握表达式的变换方法在数字电路识别中同样是很重要的。例如,对于下面逻辑函数的四种表达式则对应四种不同结构的逻辑电路,如图4-22所示。
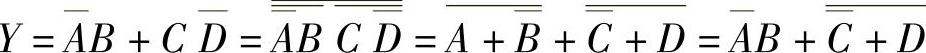
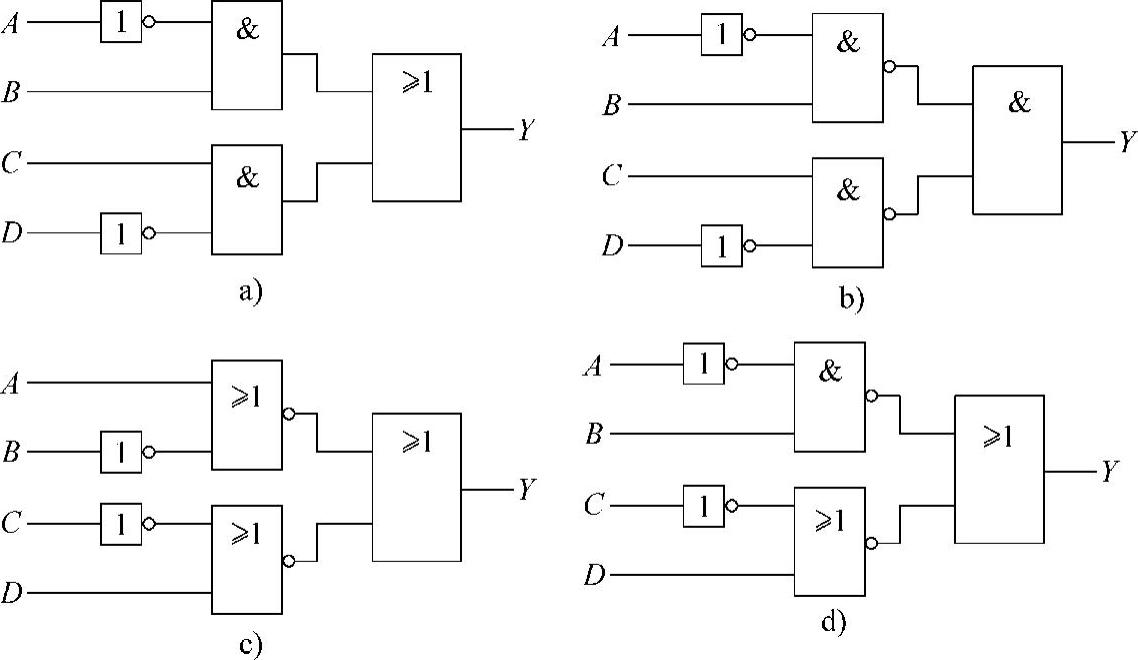
图4-22 Y函数的四种逻辑电路
4.按逻辑图写出表达式
按逻辑图写出逻辑函数的表达式是读识数字电路的第一个重要步骤。
(1)由电路的输入端入手。由电路的输入端入手写逻辑表达式时,是从电路的输入端开始依次在各逻辑门的输出端写出它的运算结果,当写到电路的输出端时完整的逻辑表达式也就出来了。此方法如图4-23所示。
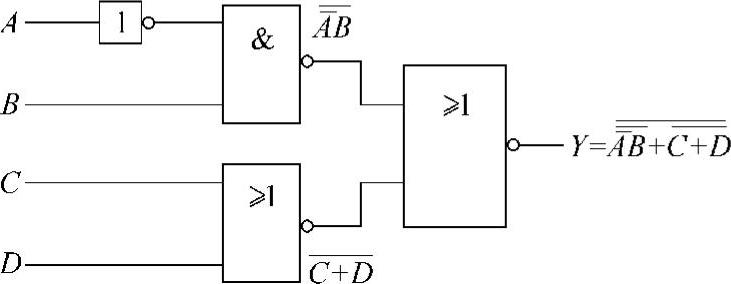
图4-23 由电路的输入端入手写逻辑表达式
电路的逻辑表达式为
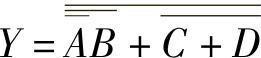
(2)由电路的输出端入手。由电路的输出端入手写逻辑函数的表达式时,是先给电路中的各逻辑门的输入信号赋予一个临时代号,再从输出端入手依次把各个逻辑门表示的逻辑运算关系逐层代入,一直推写到输入端,完整的表达式就出来了。此方法如图4-24所示。
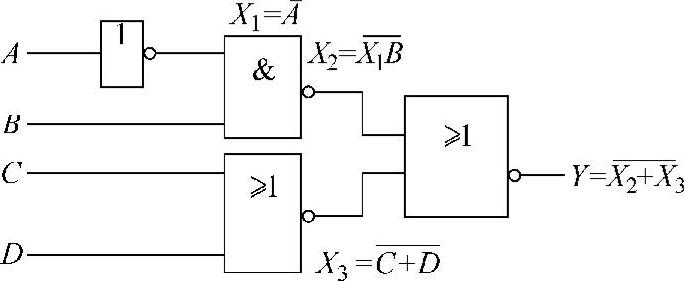
图4-24 由电路的输出端入手写逻辑表达式
电路的逻辑表达式为
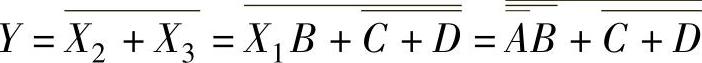
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




