自由基分子自旋极化输运性质研究

图5.2（a）画出了两种苯氧基的平行磁化结构（PC）和反平行磁化构型（APC）的电流-电压（I-U）曲线。PC（APC）的情况是表示两个苯氧基的自旋方向平行（反平行）。对于PC情况，少数自旋电流（IPC，min）随着偏压线性增加，到0.20V附近电流值达到峰值，然后在0.24V左右突然下降。在0.24V之后，少数自旋电流缓慢降低，在0.44V左右，少数自旋电流数值达到谷底。当前NDR效应的峰谷值（PVR，电流峰值和电流谷底值之间的比率）为434%。计算结果显示，多数自旋电流（IPC_maj）被抑制，数值上总是比少数自旋电流小得多。对于APC情况，少数自旋电流也线性增加，到0.18V左右达到峰值，然后缓慢降低，到0.40V左右到达谷底。其中，NDR效应的峰谷值达到了1304%。小于0.24V时，反平行的多数自旋电流也随着偏压增加而缓慢增加，由于上述反平行自旋电流的NDR效应，在0.24V后，反平行排列的多数自旋电流和少数自旋电流相比异常大。也就是说，NDR效应具有可以改变自旋电流的迹象，这有望未来在分子自旋电子学领域中得到应用。平行和反平行的总电流（Imin+Imaj）也同样显示了有趣的NDR效应。

自旋注入因子η[由自旋电流定义：η=（Imin-Imaj）/（Imin+Imaj），其中电导位于零偏压下]是自旋电子学器件的重要参量。图5.2（b）显示PC和APC情况的偏压依赖自旋注入因子η。由于偏压依赖自旋极化电流，PC情况下的η高达95%，然而在APC情况下，η刚开始为正，然后随着偏压增加则为负值，表明这种分子输运系统在偏压调制自旋的情况下，可用作完美的自旋滤波器和自旋注入等器件。众所周知，隧道磁阻（TMR）被定义为（IPC-IAPC）/IAPC，其中IPC和IAPC分别是平行和反平行情况的总电流。插入图5.2（b）显示了TMR与偏压之间的关系。由此可以看出，由于IPC和IAPC的NDR效应，TMR振荡并低于200%。虽然TMR不够大，但是这种分子输运系统可以用作自旋阀。

图5.2　两种苯氧基自由基分子自旋极化输运性质

从透射谱T（Ub，E），前沿分子轨道（MOS）和局部状态密度（LDOS）的行为，可以理解偏压相关的自旋极化电流和总电流。图5.3显示了零偏压下的在费米能级附近的几个分子前沿轨道及其能量。

图5.3　零偏压下在费米能级附近的几个分子前沿轨道

HOMO——Highest Occupied Molecular Orbital，代表最高分子占据轨道；LUMO——Lowest Unoccupied Molecular Orbital，代表最低分子未占据轨道

从自旋平行排列下的多数自旋通道可以看出，最高被占据分子轨道（HOMO）和HOMO-3是离域π轨道，并且完全分布在两个苯氧基上，而HOMO-1和HOMO-2是离域px轨道，而且只分布在两个O原子上。对于自旋平行排列的少数自旋通道，LUMO+1和LUMO是离域π*轨道，并且完全分布在两个苯氧基上，而HOMO（HOMO-1）是离域px轨道，主要分布在左（右）O原子。对于自旋反平行情况的多数自旋通道，LUMO（HOMO-1）是局部π*（π）轨道，并且完全分布在右（左）苯氧基上，而HOMO（HOMO-2）是局部化的px轨道并且分布在右（左）O原子。对于APC情况的少数自旋通道，LUMO（HOMO-1）也是局域化π*（π）轨道，但完全分布在左（右）苯氧基上，而HOMO（HOMO-2）也是局域的px轨道但分布在左（右）O原子上。

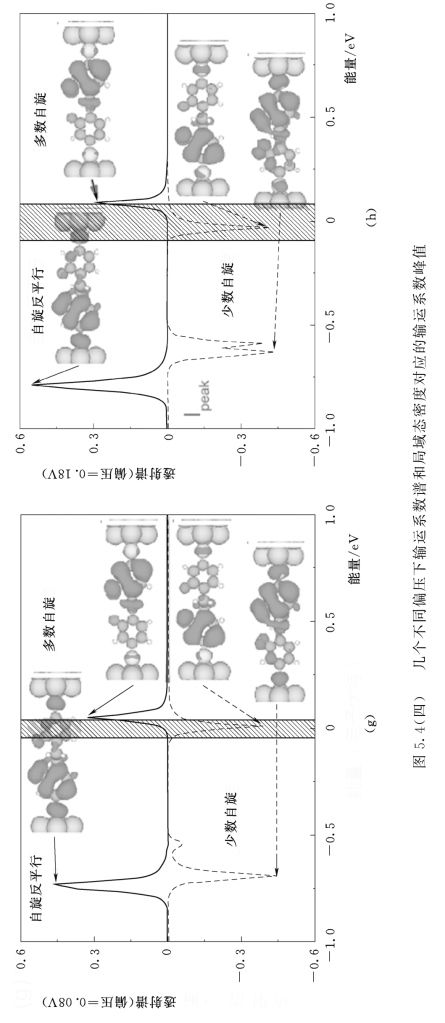
图5.4显示了对应于几个偏压下的透射谱T（Ub，E）峰值和局域态密度。首先分析自旋平行状态的输运特性。如图5.4（a）所示，在零偏压下，可以看到费米能级周围有两个Tmin（Ub，E）峰。对应于Tmin（Ub，E）峰的局域态密度（LDOS）显示，这两个峰来自于LUMO+1和LUMO的贡献。因为这两个能级是离域的，因此其在电场为0.20V以下，不能耗尽在局域轨道，所以费米能级附近的两个Tmin（Ub，E）峰几乎没有变化[图5.4（b）、（c）]，自旋平行少数电流随着偏压增大而线性增加，这是由于传输窗口的扩大所致（即偏压窗口中的传输函数的一部分积分获得电流，是从-eUb/2到+eUb/2的能量区间）。从图5.4（d）、（e）中可以看出，在偏压为0.24V和0.44V时的少数自旋通道中，位于分子上的局域化的LDOS表明，强的电场逐渐耗尽离散化的LUMO+1和LUMO到局域轨道。由于这些原因，由LUMO+1和LUMO贡献的两个Tmin（Ub，E）峰降低并彼此离开。因此，Imin减少，NDR效应显现出来。如图5.4（a）所示，在零偏压下，可以看出在费米能级以下也有两个Tmin（Ub，E）峰。对应于Tmaj（Ub，E）峰的LDOS显示这两个峰来自于HOMO和HOMO-3的贡献。当偏压增加时，这两个Tmaj（Ub，E）峰的演化与Tmin（Ub，E）的情况大致相似。由于这两个Tmaj（Ub，E）峰远离费米能级，所以反平行排列的电流（IPC_maj）被抑制并远小于平行排列的电流（IPC_min）。因此，存在强烈的自旋过滤效应。其次，分析反平行情况的输运特性。如图5.4（f）所示，在零偏压下，可以看到在费米能级以下和以上的两个Tmaj（min）（Ub，E）峰值。LDOS的分布表明LUMO和HOMO-1分别贡献了费米能级以上和以下的Tmaj（min）（Ub，E）峰值。由于局域化的LUMO和HOMO-1被σ势垒分开，所以两个Tmin（Ub，E）峰彼此接近，两个Tmaj（Ub，E）峰离开彼此。如图5.4（g）～（j）所示，由LUMO贡献的Tmaj（min）（Ub，E）峰逐渐进入输运窗口，并且大致不改变轮廓，直到在0.18V的偏压下IAPC_min峰出现，由于强电场改变了分子-电极间的耦合，Tmin（Ub，E）峰显著降低[104-106]。如图5.4（i）、（j）所示，可以清楚地看到LUMO在输运窗口中提供的LDOS在右侧巯基没有分布。因此，在0.40V的偏压下IAPC_min呈现最小值。(www.xing528.com)

在图5.1所示的分子输运系统中，当偏压施加到Au电极上时，分子上的电场大至约106 V/cm，因为两个电极之间的距离仅为1.78nm。这种电场强度足以诱导分子磁体中的磁电耦合[107-109]。研究当偏压（即电场强度）增加时，两种苯氧基的磁化结构如何演化是非常重要的。图5.5显示了部分散射区域的平行（PC）和反平行（APC）情况之间的总能量差异。由此可以看出，APC情况首先处于低于2.03×106 V/cm（Ub=0.36V）的基态，然后转移到激发态，这意味着强电场可以调控分子磁体的磁化结构。如图5.3所示，可以看出，两种不成对的电子位于PC情况中多数自旋通道中的HOMO和HOMO-1上，而APC情况位于多数和少数自旋通道的HOMO上。泡利不相容原理[110-112]可以定性地用于解释当偏压较小时APC状态为基态的原因。如上所述，在PC状态下的多数自旋通道中，HOMO和HOMO-1都是离域轨道，并且都位于两个苯氧基上。HOMO与HOMO-1之间存在能量差异，整个分子的能量增加。因此，两个不成对的电子有利于以相同的能量定位在具有不同自旋方向的两个局部轨道（APC情况）上。由于这些原因，当电场强度较小时，EPC＞EAPC，单态（APC情况）为基态。

图5.5　自旋平行和反平行情况下的能量差异

（其中EPC和EAPC分别是在自旋平行和反平行情况下散射区的全部能量）

将“自由基-自由基”分子作为整体看待，Hund规则可以定性地用于解释为什么PC状态在偏压增加时变为基态。需要4个电子来填充“自由基-自由基”分子的4个最外轨道，这4个轨道分别是自旋平行状态下多数自旋通道的HOMO和HOMO-1以及少数自旋通道的LUMO和LUMO+1。反平行状态下多数自旋通道和少数自旋通道的HOMO、LUMO。两个电子自旋向上，其他电子自旋向下。当偏压高于0.36V时，强电场将绝对耗尽离域化的HOMO（LUMO）和HOMO-1（LUMO+1）到自旋平行下多数（少数）自旋通道中的局域轨道。HOMO（LUMO）和HOMO-1（LUMO+1）只位于一个苯氧基上，并在能量空间中彼此离开。多数自旋通道中的HOMO和LUMO也在APC情况下在偏压增加时将能量空间中的少数自旋通道中的HOMO和LUMO留下。这里研究的分子输运系统具有两个不成对的电子。当这两个不成对的电子填充4个最外轨道时，它们的旋转方向倾向于平行于Hund的规则。由于这些原因，当电场强度超过2.03×106 V/cm（Ub=0.36V）时，EPC＜EAPC，三重态（PC状态）为基态。