自由基分子输运系统的结构与计算参数优化

在上述研究的驱动下，对苯氧基的稳定有机基团进行了第一性原理计算[95，96]，用于预测低偏压自旋极化负微分电阻（Negative Differential Resistance，NDR）效应的性质。NDR效应是电流在特定的偏压区域随着偏压增加而电流却减小，其具有许多应用，如频率倍增器、高频振荡器、快速开关和存储器等。计算结果清楚地表明，分子输运系统在非常低的偏压下表现出强烈的自旋极化电流NDR效应和自旋过滤效应，并且该偏压可以逆转自旋电流符号并操纵两个苯氧基的磁化构型，这有望应用在未来具有低功耗的分子自旋电子器件上。此外，分子NDR效应在未来只有在低偏压区域时才是实用的[97]，鉴于这些原因，目前的工作很有价值。

构建的分子结是双电极系统，其中两个苯氧基自由基被夹在两个Au电极之间构成了三明治结构。图5.1显示了输运系统的示意图，其中两个自由基都是苯氧基。分子与Au电极共价接触（巯基H-S键被切割）。整个输运系统分为3部分，即左电极、散射区和右电极。为了避免输运系统与其镜像之间的相互作用，沿着x和y方向，将一维Au电极放置在大的真空层。除了Au原子之外，散射区域中的所有原子位置都完全弛豫，直到最小力之容差为0.05eV/Å。通过第一性原理方法研究了输运系统的自旋转移特性，该方法将密度泛函理论（DFT）与非平衡态格林函数相结合的技术在ATK代码中得以实现[98-100]。交换关联能采用基于Perdew-Burke-Ernzerhof泛函的广义梯度近似（GGA）[101]。截断能量和k点分别设置为150Ry和1×1×50。

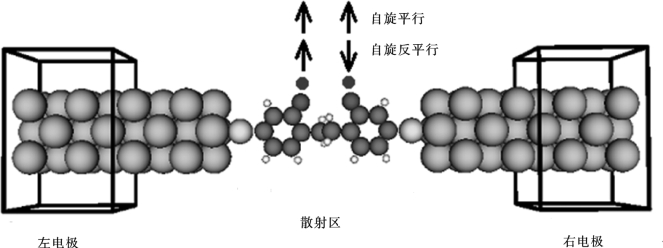
图5.1　两个Au电极和苯氧基自由基构成的双电极输运系统示意图

在计算中，使用电子温度为300K。自旋极化电流计算式为

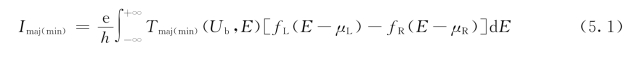
式中　fL，R——费米狄拉克分布函数，

　　　μL，R——左、右电极的化学势；

　　　h——普朗克的常数；(www.xing528.com)

　　　Ub——偏压系数；

　　　Tmaj（min）（Ub，E）——透射系数。

T（Ub，E）由下面标准方程计算，即

式中　Gmaj（min）（Ub，E）——延伸分子的自旋依赖推迟格林函数；

　　　——延伸分子的自旋依赖超前格林函数；

　　　ΓL/R——散射区域和左/右电极之间的耦合矩阵。

值得一提的是，稳态DFT[102，103]也能准确地描述分子输运系统的低偏压NDR效应和自旋过滤效应。