研究BiO（IO3）的非线性光学性质

基于密度泛函理论（DFPT），当将原子位移作为扰动时，可以计算与介电张量的变化相关的拉曼系数[63，64]。图4.5中给出了具有10.0cm-1的展宽的BiO（IO3）的计算拉曼光谱。

图4.5　具有10.0cm-1展宽的BiO（IO3）的计算拉曼光谱

可以看出，在743.01cm-1和608.13cm-1处分别有两个主峰，两个都在A1模式中。它们的模振动强度显示振动的极化方向分别沿着y轴和x轴。另外，在149.37cm-1（A1模式）、407.42cm-1（A1模式）、571.09cm-1（B2模式）和654.35cm-1（A2模式）分别存在4个相对大的峰。前3种模式的振动极化方向分别沿着y、z和y轴。从图4.5中可以看出，两个较大的峰（149.37cm-1和407.42cm-1）和两个主峰（608.13cm-1和743.01cm-1）都处于A1模式。另外两个相对较大的峰在B2模式（571.09cm-1）和A2模式（654.35cm-1）。

根据群理论，空间群Pca21属于极化点群mm2，意味着BiO（IO3）可能是性能优良的非线性光学材料的候选者。根据在参考文献[48]中报道的NLO性质的实验结果，SHG效率数据显示BiO（IO3）是I型相位匹配的，具有26pm/V的计算的〈deff〉为26pm/V。到目前为止，还没有关于电光张量的实验报告。在这项工作中，NLO系数和电光（EO）张量是基于DFPT计算的。至于用于NLO属性计算的DFPT的可靠性，已经有许多成功案例在文献中报道。例如，在参考文献[32]中，计算了各种半导体（如LiNb O3、Pb TiO3和Al As等）的NLO性质均是基于DFPT的ABINIT软件。NLO和EO系数的理论结果与实验数据之间的比较显示该方法是可靠的。在NLO系数的计算中，能量的三阶导数与电场相关，同时将离子保持在固定位置。EO张量可以从3个部分计算：电子贡献来自在夹紧的离子位置处的电场和价电子之间的相互作用；离子贡献源自电场相对于离子位置的弛豫的变化，并且压电贡献源于相反的压电效应，这是因为当允许原子移动时单位原胞的变化。为了简化dij1的记法，使用μ（μ=1、2、3、4、5、6）而不是jl（jl=11、22、33、23/32、13/31、12/21），所以diμ=dijl。根据计算结果，BiO（IO3）的非线性光学系数存在5个非零元素，即d15、d24、d31、d32和d33。(www.xing528.com)

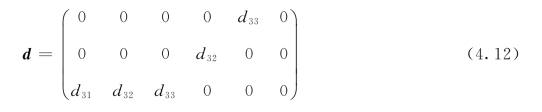
事实上，考虑到Kleinman的对称性[65]，由于d15=d31和d24=d32，只有3个独立元素。d31、d32和d33的计算值分别为12.18pm/V、5.06pm/V和18.34pm/V。对于EO张量，存在5个独立元素，即γ13、γ23、γ33、γ42和γ51。

计算的总EO张量元素γ13、γ23、γ33、γ42和γ51分别为36.21pm/V、2.28pm/V、44.54pm/V、1.43pm/V和87.61pm/V。因为LDA低估晶格参数和晶胞体积，计算结果和实验值之间存在一些差异。此外，赝势和交换相关电位也可能对结果产生一定的影响并带来一些偏差。期待更多的NLO属性的实验数据，可以用于计算的参考。上述结果表明，碘酸盐BiO（IO3）是一种有希望的高性能非线性光学晶体。