研究BiO(IO3)的介电和压电性质

BiO（IO3）的空间群Pca21属于极点mm2，然而测得的频率依赖极化曲线没有显示电滞回线，这可能归因于介电损耗[48]。该晶体内部存在显示局部极性的氧多面体：观察到BiO6的极化反转（4个Bi-O1和两个Bi-O2键），然而极化反转对于IO3（I-O2、I-O3和I-O4键）多面体在能量稳定上是非常不利的。通过对BiO（IO3）应用原子位移和均匀电场计算线性响应，可以得到Born有效电荷张量为

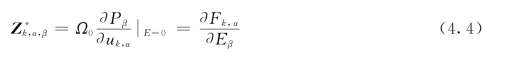
式中　Z*——由沿着具有零宏观电场的α方向的与子晶格k相关的原子的位移，或由沿着β方向的宏观电场在原子上相关的力引起的每单位晶胞的极化P；

　　　Ω0——单位晶胞体积。

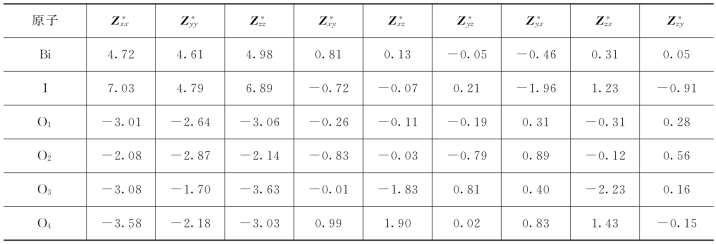
自两个不同扰动的计算的Z*几乎完全相等，在表4.2中给出这些结果。因为Z*可以显示每个原子的键性质相对于其标称离子值的共价，这可以帮助理解铁电的起源。Bi、I和O的标称离子值分别为+3、+5和-2。通过比较这些离子值与Z*，发现I（xx和zz分量）、O3（zz分量）和O4（xx分量）的Z*显然远远比其他原子异常，虽然Z*的Bi、O1和O2原子与离子值相比也是异常的。由于BiO（IO3）的晶体结构显示各向异性，因此Z*的非对角元素不为零，并且不同O原子的相同组分的许多元素显示相反的符号。

表4.2　极化氧化物BiO（IO3）基于LDA计算的波恩有效电荷

通过使用基于现代极化理论的有限电场法计算BiO（IO3）的电极化。总极化强度P被分为离子极化（Pion）和电子极化（Pele）。沿着x轴和y轴所获得的Px和Py的值几乎为零，然而沿着z轴，单位晶胞的计算的电极化Pz为23.42μC/cm2，Pion和Pele分别为10.35μC/m2和13.07μC/m2。根据参考文献，偶极矩（μ）计算（在单位晶胞中）显示∑BiO6E和∑IO3E（E=孤对电子）多面体的偶极矩值（μx，μy和μz）分别为（0.00，0.00，4.82）和（0.00，0.00，58.50）；BiO（IO3）的晶胞中的∑μz的偶极矩值为63.32。显然，沿着x轴和y轴，单位原胞的总偶极矩被抵消；只有沿z轴有一个大的净极化。本研究的理论结果与文献[48]获得的偶极矩结果一致，由于BiO6和IO3多面体中的孤对电子，净极化主要沿z轴。然而，对于铁电行为，参考文献[10]中的频率相关的极化测量显示无电滞回线，可能的原因是介电损耗。尽管未观察到BiO（IO3）中的电滞回线，当用激光照射该化合物时，由于沿z轴的每单位晶胞的净极化，其可具有相当大的SHG响应。

根据群理论分析，BiO（IO3）在Г点的所有对称适应模式被分为4个不可约表示，即

其中，3个零频率声模式分别为A1、B1和B2中的一个。因此，存在17A1、18A2、17B1和17B2光学声子模式。值得注意的是，A1、B1和B2光学模式是拉曼和红外（IR）活性，而A2光学模式只有拉曼活性。在离子晶体中，长波光波产生极化电场，其将增加纵波的恢复力。因此，纵波的频率将增加。化合物的静态介电常数总是大于高频介电常数，因此离子化合物的纵向光学（LO）晶格振动的固有频率总是大于横向光学（TO）晶格振动的固有频率长波长。LO和TO频率之间的分离通过Lyddane-Sachs-Teller（LST）关系精确描述[62]。一般来说，Born有效电荷越大，LO-TO分裂越大。该化合物的横向区域中心光声子频率列于表4.3中。

表4.3　化合物的横向区域中心光声子频率

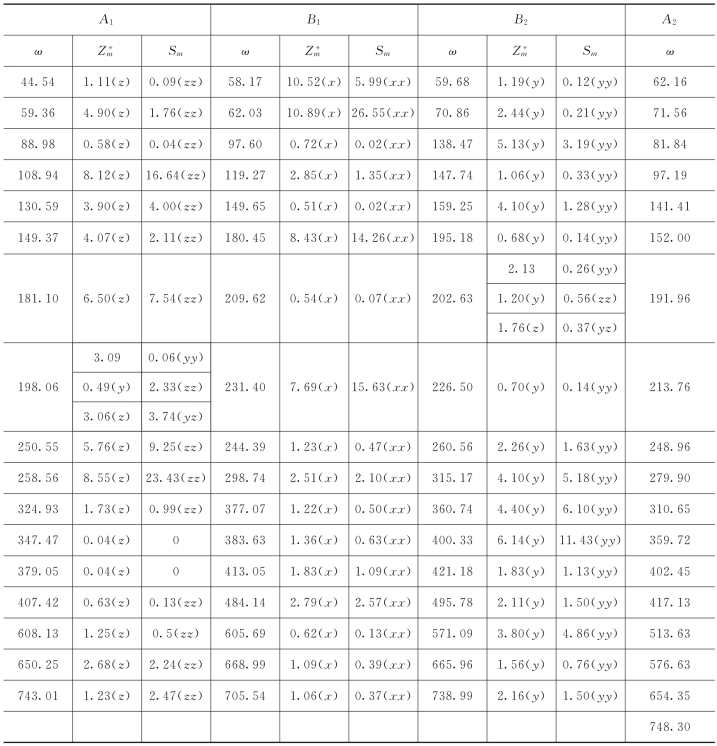
如先前关于Born有效电荷所讨论的，通过将这些离子值与Z*进行比较，可以发现I（xx和zz分量）、O3（zz分量）和O4（xx分量）的Z*明显比其他原子异常。通过对具有大的LO-TO分裂的相应频率执行振动分析，发现在这些模式中，相应的特征主要来自I和O原子。这与以前对Born有效电荷的分析是一致的。计算出的ν（I-O）的IR吸收光谱峰值分别为705.54cm-1（B1模式）和608.13cm-1（A1模式）；对于ν（Bi-O），结果为495.78cm-1（B2模式）和383.63cm-1（B1模式）。先前报道的实验数据是ν（I-O）为764cm-1和695cm-1，ν（Bi-O）[48]为510cm-1和404cm-1。为了更清楚地显示这些模式的性质，根据每个模式在笛卡儿坐标系中的特征位置计算每个原子的位移矢量。ν（I-O）和ν（I-O）的一些结果分别显示在图4.4（a）～（d）中。在图4.4中，箭头表示光学有源振动模式中相应原子的振动方向。图4.4（a）、（b）示出了705.54cm-1（B1模式）和608.13cm-1（A1模式）的IR谱值的振动方向。箭头表明这两种模式主要来自I和O原子。得到的495.78cm-1（B2模式）和383.63cm-1（B1模式）的IR振动谱如图4.4（c）、（d）所示。箭头表示这两种模式主要来自Bi和O原子的振动。

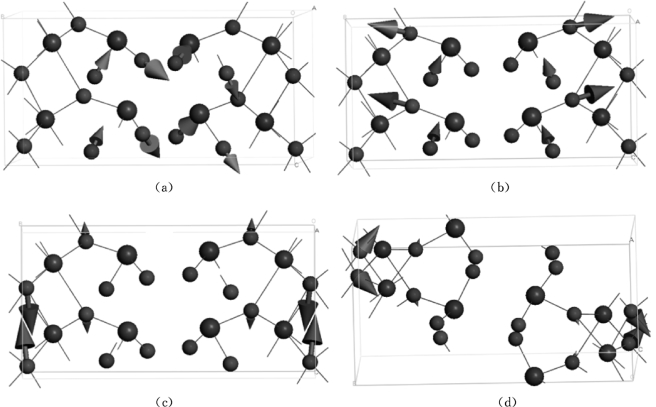
图4.4　部分IR活性声子模式的振动分析

表4.3所列碘酸盐BiO（IO3）的横向光学分支A1、A2、B1和B2的振动模式频率（cm-1），模有效电荷（|e|）和模式振动强度（以10-4原子单位），纵向光学A1、B1和B2模式也显示在表4.3中。

另外，注意到大的振动位移主要来自I-O和Bi-O键之间的O原子。理论结果基本上与实验数据一致，特别是模式的相同定性趋势。理论和实验之间的前两种模式的相对大的差异可以归因于与实验相比在LDA中计算的更小的晶格参数，理论和实验之间的差异的其余部分可能是由于在计算中涉及交换相关关联势和局域密度近似。

碘酸盐BiO（IO3）的介电常数可以基于Born有效电荷和中心区域声子频率计算。静态电介质响应分为电子贡献（）和晶格贡献，即

式中　α，β——轴坐标，α、β=x、y、z；(www.xing528.com)

　　　Sm，αβ——模式振动强度，Sm，αβ=PmαPmβ；

　　　Pmα——具有频率为ωm和特征向量为ξm的声子模；

　　　Ω0——单位晶胞的体积。

模有效电荷等于。碘酸盐BiO（IO3）的空间群是Pca21，属于双轴晶体。由于对称性，沿着3个不同轴的介电常数不同。得到的LDA的光电介质张量分别为5.01、4.68和5.12。此外，基于GGA计算的值分别为4.98、4.74和5.14。相应地，在LDA内计算的折射率nx、ny和nz的分别为2.373、2.268和2.395。在双轴晶体中，εxx≠εyy≠εzz导致n1≠n2≠n3。折射率椭球方程为

假设n1＜n2＜n3，折射率椭圆体和x1Ox3平面的交点轨迹为椭圆，其方程为如果椭圆上任何点和x1之间的角度为ψ，这个方程可以写成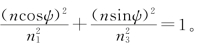因为n1＜n2＜n3，所以可以总是找到半径向量r0，其长度等于n2。显然，平面（由半径向量r0和x2组成）和折射率椭球之间的横向是半径为n2的圆。如果C是圆的法线方向上的单位矢量，则在双轴晶体中存在两个光轴方向（如命名为C1和C2）。C1/C2和x3之间的角度值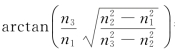等于66.48°（＞45°），因此，BiO（IO3）是一个负双轴晶体。此外，虽然电子响应通常在实验数据，因为来自晶格贡献的静态响应的精度比电子响应大约一个数量级，该误差可以忽略不计，BiO（IO3）的静态电介质张量元素和是120.55、110.61和123.70，在GGA中，对应值分别为120.15、112.48和124.51。模式有效电荷和LDA中模式m的模式振动强度Sm，αβ也列在表4.3中。对于静态介电张量，3个A2模式（81.84cm-1、248.95cm-1、29.90cm-1）和4个B2模式（59.68cm-1、147.74cm-1、195.18cm-1和495.78cm-1）具有大模有效电荷和振动强度，因此，主要贡献来自4个A1模式（149.37cm-1、258.56cm-1、347.47cm-1、743.01cm-1）、两个A2模式（62.16cm-1、576.63cm-1）、两个B1模式（97.60cm-1、298.74cm-1）和在所有模式中具有较大模有效电荷和振动强度的3种B2模式（400.33cm-1、571.09cm-1、607.18cm-1），主要贡献来自两个A1模式（181.10cm-1、250.55cm-1）、4个B1模式（149.65cm-1、209.62cm-1、231.40cm-1、605.69cm-1）和两个B2模式（70.86cm-1、138.46cm-1）。

使用均匀应变作为基于DFPT的微扰，计算BiO（IO3）的弹性和压电常数。结果表明，其有9个独立的非零元素，即C11、C12、C13、C22、C23、C33、C44、C55和C66。

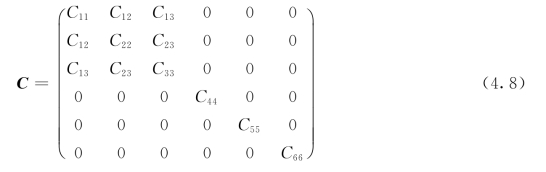
基于斜交晶的Born机械稳定性标准[40，41]，BiO（IO3）的限制应满足：

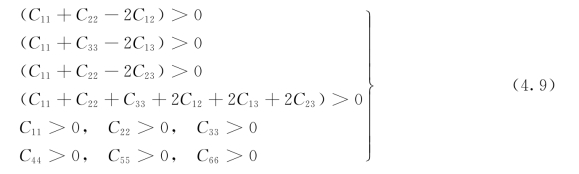
计算结果为弹性硬度张量常数，见表4.4。注意参考文献[42]中的最新报告，斜方晶系统中必要且充分的弹性稳定性条件为

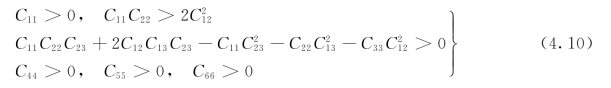
根据上述计算结果，发现LDA和GGA的弹性硬度张量元素都能满足方程中的Born稳定性限制，因此该化合物机械稳定。

表4.4　计算的BiO（IO3）的弹性硬度常数

对于压电应力张量，该化合物有5个独立的非零元素e15、e24、e31、e32和e33，即

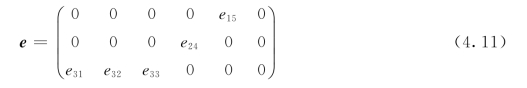
表4.5给出了LDA和GGA中BiO（IO3）的相应的松弛离子压电应力张量。根据参考文献[48]的实验结果，发现压电常数d33（位移对电场）大约为26pm/V，这与其他碘酸盐如LiIO3（d33=92pm/V）和KIO3（d33=39pm/V）具有一定的可比性。注意，d33压电常数属于可逆压电常数。当向压电材料表面施加电场（电压）时，电偶极矩由于电场而被拉伸。抵抗变化的压电材料将沿电场方向拉伸。这种由机械变形产生的电场的过程称为“反向压电效应”。反压电常数（dmi）、压电应力常数（emj）和弹性柔性常数（sij）具有的关系（SE是电场E=0时的短路弹性柔性常数），因此d33=s31e31+s32 e32+s33 e33。LDA内的计算弹性柔性常数s31、s32和s33分别为-2.16MPa-1、-2.71MPa-1和7.56MPa-1。根据在表4.5中给出的压电应力常数的值，获得的d33=27.11pm/V，这与实验结果非常一致。大的压电常数表明，BiO（IO3）是一种高性能无铅压电材料。

表4.5　计算的BiO（IO3）的压电常数