BiO(IO3)的晶体结构和计算参数简介

2011年，Nguyen等人[48]通过利用水热法，将Bi（NO3）·5H2 O、HIO3和HNO3合成了一种新的极性碘酸盐BiO（IO3），其包含两对阳离子，即Bi3+和I5+。该化合物的空间群Pca21是属于极性点群mm2，结构上包含与（IO3）阴离子和（BiO2）2+阳离子连接的层状结构（图4.1）。作为一种多功能NCS复合物，Nguyen等人还测量了BiO（IO3）的极化强度、红外光谱和压电性能。实验数据表明，该化合物不仅是一种有希望的压电材料，而且是具有大的二次谐波产生（SHG）响应的潜在的非线性光学晶体[48]。

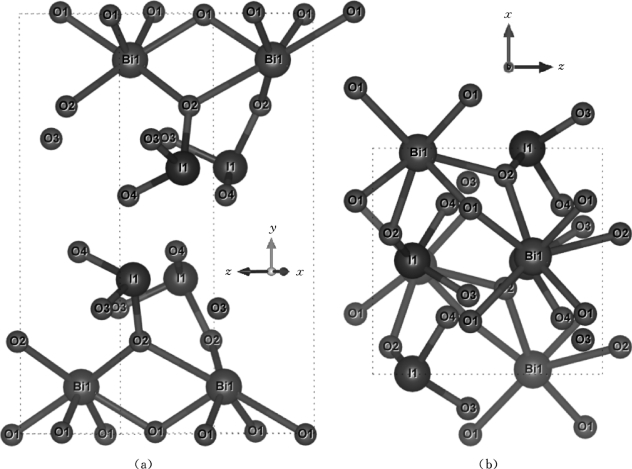
图4.1　BiO（IO3）沿着y轴的晶体结构示意图和沿着x-z平面的俯视图

在合成NCS化合物方面，孤对阳离子Bi3+和I5+已经引起了研究者很大的关注。然而，含有两种孤对阳离子的材料是非常罕见的，迄今为止仅报道了少量这种类型的化合物，如TeSeO4、PbSeO5、BiSeO5、BiSeO3 Cl和Bi TeO5[49-51]。该类材料需要从理论或实验研究中充分理解它们的电子性能。如今，基于密度泛函理论的第一性原理方法已成为准确预测新材料特性的有力工具，理论结果可用于解释或确认实验结果，得出更有说服力的结论。在Nguyen等人[48]的工作中，计算了BiO（IO3）的电子态密度。结果表明，存在大约2.0eV的带隙，并且上部价带具有来自O2-sp态的显著贡献，其中来自I-5 sp和Bi-6 sp态的贡献较小，因为I5+和Bi3+包含孤对电子。然而，到目前为止，在文献中没有关于这种类型的化合物的电介质、压电和非线性光学性质的详细理论报告。

本章主要研究最近合成的极性碘酸盐BiO（IO3）。通过开展第一性原理DFT计算，系统地研究其电子结构、晶格动力学、电介质和压电性质。BiO（IO3）（Pca21）的空间群属于极化点群[52-54]，该点群的材料通常具有非线性光学性质。为了研究其非线性光学性质，采用基于2n+1电场依赖理论计算了该材料的非线性光学系数和电光张量。将理论结果与可用的实验数据进行比较，发现两者有良好的一致性。

在计算中主要使用ABINIT软件[55，56]。对于几何优化和基态电子结构计算，使用基于ABINIT的保守赝势和投影增强波（PAW）方法[57-59]来描述离子，平面波截止能量为45Ha。此外，基于维也纳从头计算软件包（VASP）的Vanderbilt超软赝势计算能带结构和Mulliken电荷数。赝势中电子中的价电子如下：Bi 6s，6p电子、I 5s，5p电子和O 2s，2p电子。平面波截断能为40Ha，8k×8k×8k点网格，交换关联势为GGA[60]。晶格动力学和非线性光学性质的计算基于Troullier-Martins模守恒赝势[61]和局域密度近似（LDA）。许多物理性质与对干扰的电子响应有关，如原子位移、应变和电场。线性和非线性响应可以由DFPT详细描述。考虑二阶应力张量（σ）和二阶应变张量（η）之间的关系，材料的四阶弹性常数（C）定义为

(www.xing528.com)

其中i和j（1～6）表示笛卡儿坐标方向。字母xx、yy、zz、yz、zx和xy分别被数字1～6替代（即i、j）。对于某些固体材料中的压电系数eαi，可以响应于施加的机械应力来计算三阶压电应力张量，即

其中α是极化方向，并且i=1～6表示具有电场E=0的笛卡儿方向。在绝缘体中，利用泰勒展开，极化和宏观电场之间的关系可以得到包括零场的自发极化、线性介电常数和二阶非线性光学系数。为了获得非线性光学性质，利用基于2n+1理论的三阶能量函数，该计算只需要第一阶波函数。考虑3个埃米特扰动（λ1、λ2、λ3），能量混合的第三阶导数可以从基态波函数计算出结果。对于非线性光学系数，只考虑电子的贡献（在夹紧位置的离子）和低频电场的能量的三阶导数。在二阶非线性光学性质的实际计算中，仅考虑电子的贡献并将离子保持在固定位置。在NCS化合物中，与电场成线性比例的折射率的变化称为主电光（或普克尔斯）效应。由低频电场引起的折射率（n）的变化为

式中　rij——线性电光张量（i=1～6，j=1～3）；

　　　εj——电场。

电光张量来自电子、离子和压电贡献。应当注意，由于逆压电效应，压电贡献源自单元电池的弛豫。