众所周知,晶体(crystal)是有明确衍射图案的固体,其原子或分子在空间按一定规律周期重复地排列。晶体中原子或分子的排列具有三维空间的周期性,隔一定的距离重复出现,这种周期性规律是晶体结构中最基本的特征。晶体内部结构中的质点(原子、离子、分子、原子团)有规则地在三维空间呈周期性重复排列,组成一定形式的晶格,外形上表现为一定形状的几何多面体。晶体的理想外形或其结构都是对称图像。这类图像都能经过不改变其中任何两点间距离的操作后复原。这样的操作称为对称操作,平移、旋转、反映和倒反都是对称操作。能使一个图像复原的全部不等同操作,形成一个对称操作群。在晶体结构中空间点阵所代表的是与平移有关的对称性。此外,还可以含有与旋转、反映和倒反有关并能在宏观上反映出来的对称性,称为宏观对称性,它在晶体结构中必须与空间点阵共存,并互相制约。空间点阵由3条不重合的矢量构成的空间重复单元构成,这种空间单元只具有7种形式,分别为三斜、单斜、正交、四方、三方、六方、立方三角晶系。
根据晶体的对称性,七大晶系分别对应14种布拉菲格子、32个点群和230个空间群。在32个点群中间,其中有21种非中心对称点群和10种中心对称点群。在固体物理中,点群与晶类(crystal class)有等同的含义。点群与对称要素和对称操作群两个概念有关。对称操作群是由物体的对称操作构成的群。对称操作即物体在正交变换(保持两点间距离不变的几何操作,如旋转、反伸、反映)下不变,则该变换为物体的对称操作。群的数学概念为集合和其上的一种运算构成一个群。群要求满足封闭性,存在单位元素和逆元素,满足该运算的结合律;简单地说,群是按照某种规律相互联系着的一组元素的集合。群的元素可以是字母、数字等,在晶体对称理论中,群的元素是对称操作。对称要素包括对称中心、对称轴、对称面、旋转反伸轴和旋转反映轴。对称要素可用普通符号、国际符号和Schoenflies符号3种方式表示。可以证明,晶体中对称要素共有8种,分别是1、2、3、4、6、m、i、-4(这里用国际符号表示,准晶中还可以出现其他对称要素)。对称轴是一根假想直线,n重旋转轴是指若物体绕某轴转2π/n及2π/n的整数倍,物体不变,则该轴为物体的n重旋转轴。
有了点群的划分,就可以表示任何一种晶体具体的结构对称性。点群的国际符号一般由3位组成,分别表示3个特定方向上的对称元素,不同晶系中3个方向的选取自然不同,如钛酸钡的六方晶系就可表示为6/mmm。晶体内部结构中全部对称要素的集合称为“空间群”。一切晶体结构中总共只能有230种不同的对称要素组合方式,即230个空间群。它是由俄国结晶学家费多洛夫和德国结晶学家薛弗利斯(Artur Moritz Schoenflies,1853—1928)于1890—1891年间各自独立地先后推导得出来的,故也称为“230个费多洛夫群”。空间型和对称型(点群)体现了晶体内部结构的对称与晶体外形对称的统一。每个对称型有若干个空间群与之相适应,即外形上属于同一对称型的晶体,其内部结构可分属于若干空间群。空间群可以分为两类:一类称为简单空间群或称点空间群;另一类称为复杂空间群或称非点空间群。
点空间群是由一个平移群和一个点群对称操作组合而成的,它的一般对称操作可以写成[R|t(αβγ)],其中R表示点群对称操作,t(αβγ)表示平移操作。具体分析表明,共有73种不同的点空间群。理想的完整晶体应是无限大的,点阵单元在空间3个方向上的无限平移将给出整个点阵。或者说,无限的点阵在平移下保持不变。所以平移也是一种对称操作,它的对称要素不是一个轴、一个点、一个面,而是整个点阵。(https://www.xing528.com)
与平移有关的对称要素有3个:①点阵,与其相应的操作是平移;②螺旋轴,相应的操作是转动和平移组成的复合对称操作;操作进行时,先绕一轴转动一定角度,然后再沿与此轴平行的方向进行平移(或先平移再转动),螺旋轴的轴次也只有1、2、3、4和6,对于n重螺旋轴,沿轴向的平移,应符合晶体的周期性要求;③滑移面,相应的操作是镜像和平移组成的复合操作;操作进行时,先通过某一平面进行镜像,然后再与平面平行的方向上平移一定距离,该平面就称滑移面。应该注意,与点阵、螺旋轴、滑移面对应的对称操作,空间上的每一点都移动了,具有这种性质的操作称为空间操作。因为空间操作直接与晶体微观结构的周期性相联系,故也称微观对称操作,其阶为∞。与空间操作相对应的对称操作要素只能存在于无限的结构中,而不能存在于有限的晶体中。包括了这些与平移有关的操作之后,晶体的对称运动可以全部分类成230个对称操作群,称晶体空间群,也称空间群。
对于铁电性,化合物需要离子或电子的对称破缺。这意味着它们应属于21个非中心对称晶体类中的10个极化点群(1、2、3、4、6、m、mm2、4mm、3m、6mm)中的一个。晶体的物理性质和非中心对称化合物(NonCentro Symmetric compounds,NCS)类别之间的相互关系显示在图1.1中[3]。非中心对称材料可以具有一些或全部以下性质:对映异构体(Enantiomorphism)、旋光性(即圆二色性)、压电性能和热电性能。需要注意的是,二阶非线性光学(Non Linear Optical,NLO)行为,即二次谐波产生(Second-Harmonic Generation,SHG)具有与压电性相同的对称性要求。有一些有趣的相互关系发生在对称相关属性之间。例如,所有热释电具有SHG行为,但是反过来却不成立。对映异构晶体存在于11种点群类别,分别为1(C1)、2(C2)、3(C3)、4(C4)、6(C6)、422(D4)、222(D2)、622(D6)、32(D3)、23(T)和432(O),所有这些材料都是光学活性的(即圆二色性原理)。只有点群1(C1)、2(C2)、3(C3)、4(C4)和6(C6)具有所有对称性相关属性。
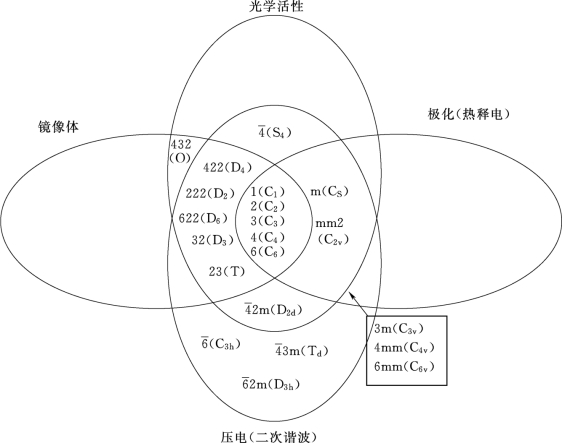
图1.1 国际符号海尔曼-摩根(Hermann-Mauguin)和申弗利斯(Schoenflies)符号的非中心对称晶体的相互关系[3]
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




