建立热冲压成形工艺传热数学模型的方法

运用解析方法所得到的解为分析解，是以数学分析为基础求解导热定解问题，代表了求解区域内的温度分布，并在所有内点上精确地满足导热方程，在边界上满足规定的边界条件，又称为精确分析解。

（1）钢板解析法传热数学模型的基本假设 由于建立钢板的解析法模型涉及非稳态传热的基本定律，基于研究可行性与方便考虑，简化模型，并做一定基本假设。

1）鉴于热力耦合模拟的复杂性及带来的冷却效果参数的不可变性，忽略冲压过程中的钢板变形。

2）将模型简化为空气、钢板、模具组成的封闭模型，与外界没有热交换。

3）钢板传热的各向同性。

4）由于钢板厚度相比钢板长宽相差两个数量级以上，将钢板简化为一维大平壁传热模型。

（2）钢板解析法传热数学模型的基本方程 根据传热理论，钢板的毕渥数Bi＜0.1，即钢板内部温差基本可以忽略。按照集总热容系统得非稳态导热系统为钢板建立传热数学模型。

根据热平衡规律及能量守恒定律，钢板的导热能量方程为^[86]

式中，ρ为体积质量（密度）；c为比热容；A和V为钢板的表面积和体积；q为钢板边界面的热流密度；n为边界面的单位外法向矢量；q_V为钢板内热源的发热率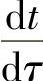；为温度分布，t为温度，τ为时间。

式（8-13）中等号右边第一项代表整个边界面与钢板的换热热流量Q，第二项代表内热源产生的热量Q_V。

（3）不同边界条件下的钢板解析法传热数学模型 以钢板为研究对象，运用非稳态传热的基本理论，建立三个阶段下的解析数学模型。考虑到第二阶段耦合了第一阶段和第三阶段的传热特点，故将第二阶段放在最后进行描述。

1）第一阶段（钢板空气对流及辐射换热阶段）钢板的传热数学模型。钢板从加热炉中取出，到达模具实行固体淬火前，钢板冷却主要为空气对流换热和辐射换热。此时

q=α（T-T_f） （8-14）

式中，T_f为环境温度；α为整个钢板边界上的平均换热系数，包括空气对流换热系数和辐射换热系数，α=α_c+α_r。

由于无内热源，q_V=0，于是式（8-13）简化为

式中，ρ为体积质量（密度）；c为比热容；A和V为钢板的表面积和体积；q为钢板边界面的热流密度；n为边界面的单位外法向矢量；q_V为钢板内热源的发热率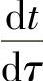；为温度分布，t为温度，τ为时间。

式（8-13）中等号右边第一项代表整个边界面与钢板的换热热流量Q，第二项代表内热源产生的热量Q_V。

（3）不同边界条件下的钢板解析法传热数学模型 以钢板为研究对象，运用非稳态传热的基本理论，建立三个阶段下的解析数学模型。考虑到第二阶段耦合了第一阶段和第三阶段的传热特点，故将第二阶段放在最后进行描述。

1）第一阶段（钢板空气对流及辐射换热阶段）钢板的传热数学模型。钢板从加热炉中取出，到达模具实行固体淬火前，钢板冷却主要为空气对流换热和辐射换热。此时

q=α（T-T_f） （8-14）

式中，T_f为环境温度；α为整个钢板边界上的平均换热系数，包括空气对流换热系数和辐射换热系数，α=α_c+α_r。

由于无内热源，q_V=0，于是式（8-13）简化为

假定环境温度T_f保持常量，则T_f=T∞。引入过余温度θ=T_i-T，其中T为钢板的初始温度，T_i为i时刻钢板的温度，T∞为钢板冷却最终温度。于是式（8-15）为

假定环境温度T_f保持常量，则T_f=T∞。引入过余温度θ=T_i-T，其中T为钢板的初始温度，T_i为i时刻钢板的温度，T∞为钢板冷却最终温度。于是式（8-15）为

初始条件为

t=0时，θ=θ∞=T_i-T_f=0 （8-17）

令C=ρcV和R_α=1/（αA）分别代表钢板的总热容量和总热阻，则式（8-16）变为

初始条件为

t=0时，θ=θ∞=T_i-T_f=0 （8-17）

令C=ρcV和R_α=1/（αA）分别代表钢板的总热容量和总热阻，则式（8-16）变为

式（8-18）的通解为

式（8-18）的通解为

其中，等号右边第一项为方程对应齐次方程的通解，等号右边其余项为方程的一个特解。利用初始条件即式（8-17），确定待定常数为c₁=-θ∞。将其带入式（8-19），得到式（8-15）的解为

其中，等号右边第一项为方程对应齐次方程的通解，等号右边其余项为方程的一个特解。利用初始条件即式（8-17），确定待定常数为c₁=-θ∞。将其带入式（8-19），得到式（8-15）的解为

还原为钢板温度变量：

还原为钢板温度变量：

式（8-21）表明，在对流换热和辐射换热条件下，钢板温度随时间成指数关系变化。在冲压刚开始阶段，温度变化较快，而后逐渐减慢，最终与环境温度达到一致。钢板温度随时间变化曲线由钢板的总热容量及钢板与环境间的总热阻来决定。

2）第三阶段（钢板模具间导热）钢板的传热数学模型。变形阶段结束，钢板进入热冲压工艺的保压阶段，此时，钢板两边为纯固体淬火的冷却状态，即第三阶段。

由于现尚无有关固体淬火冷却理论，本书提出等效表面传热系数，基于固体淬火工艺和冷却水对流换热的淬火工艺中，传热方式不同，但热流密度一致的特点，将固体淬火的传热模式转化为等效的水冷淬火。

在固体淬火冷却条件下，钢板通过与凹模直接接触导热。由于接触热阻的存在，接触面上有明显的温降，热流在此处发生收缩。为了便于研究，做出以下等效转换^[87]。

将接触热阻假设成为具有所需厚度的钢板，该钢板厚度为

l=R_fλA （8-22）

式中，R_f为钢板与凹模间的接触热阻；A为钢板与凹模间的接触面积；λ为钢板的导热系数。

该钢板与被冷却钢板之间无接触热阻，为纯固体导热。

将固体淬火等效为具有相同冷却效果的对流换热冷却。

由于如果直接应用固体传热与热阻概念计算，将得到难以转化的非齐次方程组，故提出等效表面传热系数概念，将非齐次方程组转化为齐次方程组，即将固体淬火转化为具有相同冷却效果的对流换热冷却。不同的传热方式下，热流密度是一致的。在冷却水对流换热条件下，热流密度（表面传热系数）为

q=α（T-T_f） （8-23）

固体淬火方式下：(www.xing528.com)

式（8-21）表明，在对流换热和辐射换热条件下，钢板温度随时间成指数关系变化。在冲压刚开始阶段，温度变化较快，而后逐渐减慢，最终与环境温度达到一致。钢板温度随时间变化曲线由钢板的总热容量及钢板与环境间的总热阻来决定。

2）第三阶段（钢板模具间导热）钢板的传热数学模型。变形阶段结束，钢板进入热冲压工艺的保压阶段，此时，钢板两边为纯固体淬火的冷却状态，即第三阶段。

由于现尚无有关固体淬火冷却理论，本书提出等效表面传热系数，基于固体淬火工艺和冷却水对流换热的淬火工艺中，传热方式不同，但热流密度一致的特点，将固体淬火的传热模式转化为等效的水冷淬火。

在固体淬火冷却条件下，钢板通过与凹模直接接触导热。由于接触热阻的存在，接触面上有明显的温降，热流在此处发生收缩。为了便于研究，做出以下等效转换^[87]。

将接触热阻假设成为具有所需厚度的钢板，该钢板厚度为

l=R_fλA （8-22）

式中，R_f为钢板与凹模间的接触热阻；A为钢板与凹模间的接触面积；λ为钢板的导热系数。

该钢板与被冷却钢板之间无接触热阻，为纯固体导热。

将固体淬火等效为具有相同冷却效果的对流换热冷却。

由于如果直接应用固体传热与热阻概念计算，将得到难以转化的非齐次方程组，故提出等效表面传热系数概念，将非齐次方程组转化为齐次方程组，即将固体淬火转化为具有相同冷却效果的对流换热冷却。不同的传热方式下，热流密度是一致的。在冷却水对流换热条件下，热流密度（表面传热系数）为

q=α（T-T_f） （8-23）

固体淬火方式下：

式中，T_m为凹模的温度；R_f为钢板与凹模间的接触热阻。

式中，T_m为凹模的温度；R_f为钢板与凹模间的接触热阻。

可知，固体淬火方式下的等效表面传热系数为。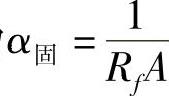

于是式（8-15）简化为

可知，固体淬火方式下的等效表面传热系数为。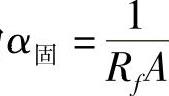

于是式（8-15）简化为

假定环境温度T_f保持常量，则T_f=T_∞。引入过余温度θ=T_i-T，其中设T_i为钢板i时刻温度。于是式（8-25）可以整理为

假定环境温度T_f保持常量，则T_f=T_∞。引入过余温度θ=T_i-T，其中设T_i为钢板i时刻温度。于是式（8-25）可以整理为

初始条件为

t=0时，θ=θ_∞=T_i-T_f=0 （8-27）

初始条件为

t=0时，θ=θ_∞=T_i-T_f=0 （8-27）

令C=ρcV和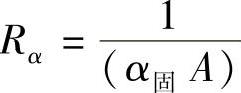分别代表钢板的总热容量和总热阻，则式（8-26）变为

令C=ρcV和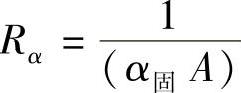分别代表钢板的总热容量和总热阻，则式（8-26）变为

式（8-28）的通解为

式（8-28）的通解为

其中，等号右边第一项为方程对应齐次方程的通解，等号右边其余项为方程的一个特解。利用初始条件即式（8-27），确定待定常数为c₁=-θ_∞。将其带入式（8-29），得到式（8-26）的解为

其中，等号右边第一项为方程对应齐次方程的通解，等号右边其余项为方程的一个特解。利用初始条件即式（8-27），确定待定常数为c₁=-θ_∞。将其带入式（8-29），得到式（8-26）的解为

还原为钢板温度变量：

还原为钢板温度变量：

式（8-31）表明，在导热条件下，钢板温度仍然与时间保持指数关系变化。钢板温度随时间变化曲线由钢板的总热容量及钢板与凹模间的总热阻决定，该总热阻由钢板与凹模间的接触热阻决定^[88]。

3）第二阶段（钢板与模具导热及与空气间对流及辐射换热阶段）钢板的传热数学模型。热冲压开始后，钢板的真实冷却状态为一边固体淬火，一边空气对流和辐射换热，整个钢板上的热流密度则可通过下式计算：

q_s=q_固+q_f （8-32）

式中，q_固为固体淬火一面的热流密度，可通过式（8-24）计算；q_f为空气对流及辐射换热一面的热流密度，可通过式（8-14）计算。

于是固体淬火和对流及辐射换热条件下的等效表面传热系数为：

式（8-31）表明，在导热条件下，钢板温度仍然与时间保持指数关系变化。钢板温度随时间变化曲线由钢板的总热容量及钢板与凹模间的总热阻决定，该总热阻由钢板与凹模间的接触热阻决定^[88]。

3）第二阶段（钢板与模具导热及与空气间对流及辐射换热阶段）钢板的传热数学模型。热冲压开始后，钢板的真实冷却状态为一边固体淬火，一边空气对流和辐射换热，整个钢板上的热流密度则可通过下式计算：

q_s=q_固+q_f （8-32）

式中，q_固为固体淬火一面的热流密度，可通过式（8-24）计算；q_f为空气对流及辐射换热一面的热流密度，可通过式（8-14）计算。

于是固体淬火和对流及辐射换热条件下的等效表面传热系数为：

采用相同的计算方法，即寻找出等效表面传热系数，将固体淬火和对流及辐射换热条件下的钢板传热数学模型转换为纯对流换热条件下的数学模型：

采用相同的计算方法，即寻找出等效表面传热系数，将固体淬火和对流及辐射换热条件下的钢板传热数学模型转换为纯对流换热条件下的数学模型：

式中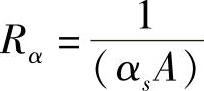，，为固体淬火和对流及辐射换热条件下钢板与凹模间的总热阻^[89]。式（8-34）表明，固体淬火和对流及辐射换热条件下钢板温度仍然随时间成指数关系变化。钢板温度随时间变化曲线由钢板的总热容量及钢板与凹模间的总热阻来决定，而该总热阻由钢板与凹模间的接触热阻及钢板与周围空气的换热能力决定。

式中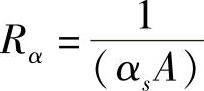，，为固体淬火和对流及辐射换热条件下钢板与凹模间的总热阻^[89]。式（8-34）表明，固体淬火和对流及辐射换热条件下钢板温度仍然随时间成指数关系变化。钢板温度随时间变化曲线由钢板的总热容量及钢板与凹模间的总热阻来决定，而该总热阻由钢板与凹模间的接触热阻及钢板与周围空气的换热能力决定。