热冲压模具冷却系统设计与优化

8.2.3.1 热冲压模具冷却系统设计

本书以图8-2所示的全封闭水冷系统模具为例，对其冷却系统的设计及其优化方法进行介绍。该模具冷却系统包括导水槽、水腔、支撑结构三部分。冷却水由凹模座一侧的进水口流入，经过导水槽，进入水腔，在支撑结构的扰动下流经水腔，完成与凹模的换热，再经导水槽流出出水口。导水槽用于冷却水的流入与流出，包括凹模座中水平水槽、竖直水槽及位于凹模座表面与凹模接触处水槽三个部分。由于冷却水速度由全程最小横截面面积决定，为了避免出现水速阻力瓶颈，接触处水槽的总横截面面积与水腔中最小横截面面积基本相同。

支撑结构在提供机械支撑的同时，增大传热面积，提供扰流条件，提高传热效率。采用组合式支撑结构，不仅可降低成本，而且可以根据需求更换。凹模与凹模座中空的楔形部分加设支撑肋，用于调节水流，将水流分散为三股，使其均布于水腔内；同时也加强了楔形部分被削弱的结构强度。凹模与凹模座中空平行部分设计支撑柱，用于引导水流走向，提供扰流条件，同时增大传热面积，提高冷却水与模具间的换热效率。支撑柱的设计也是结构强度的要求。

8.2.3.2 热冲压模具冷却系统优化

为了满足热冲压成形技术的冷却要求，冷却系统必须在满足强度要求的同时，达到最佳冷却效果。可通过理论及数值分析手段对其进行分析，以达到优化的目的。

（1）分析模型的建立 基于研究可行性与方便考虑，对研究对象做如下简化及假设：

1）以钢板中心面将钢板分为上下两部分，仅以下面一部分、模具凹模及冷却系统作为研究对象。

2）鉴于热力耦合模拟的复杂性及带来的冷却效果参数的不可变性，忽略冲压过程中的钢板变形。

3）以钢板和模具主要散热渠道为主，忽略其他热量损失，分析其热平衡状况。忽略其他热量损失包括冷却水体与凹模座的对流换热、钢板从加热炉中取出到模具开始冲压时间段的热量损失、钢板及模具在冲压过程中以热辐射形式损失的热量等。

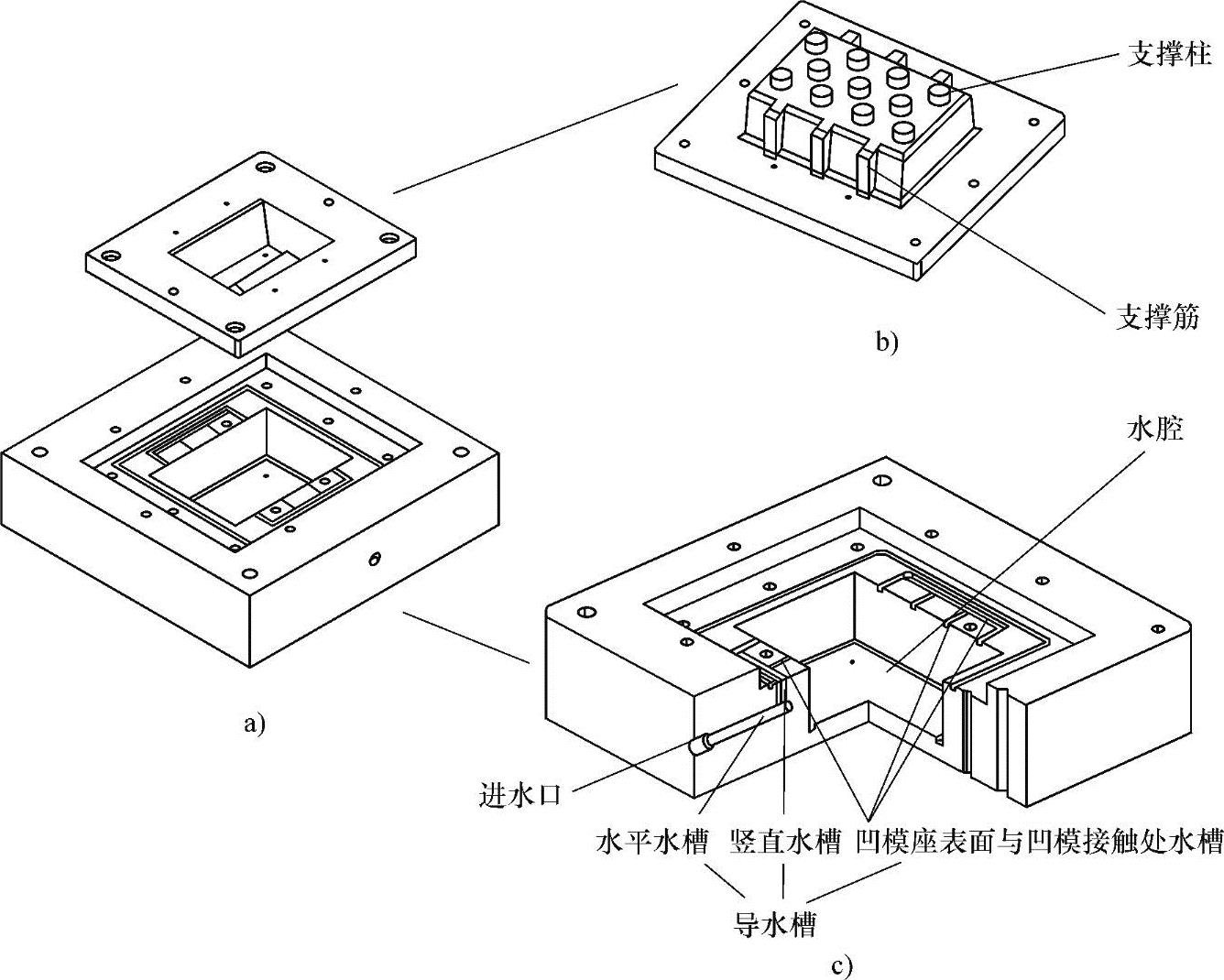
图8-2 全封闭水冷系统模具

a）凹模与凹模座组装图 b）凹模底部仰视图 c）凹模座剖视图

分析对象模型如图8-3所示。

（2）流场模型的基本方程 在该简化模型下分析其热平衡状况，主要包括钢板与凹模间的导热及凹模与冷却水之间的对流换热。假设m为钢板质量，Δt为冲压前后钢板的温度变化，A为换热面积，t_w为固体表面的温度，t_f为流体的温度。

根据传热学基本原理^[81]，冲压前后热量变化Q为

Q=cmΔt （8-2）

单位时间冷却水带走热量q为

q=hA（t_w-t_f） （8-3）

式中，c为材料比热容；h为对流换热系数。

此为该简化模型中的两个基本传热方程。

计算层流流场即求解连续性方程、N-S方程和能量方程，使用交错网格，采用SIM-PLE等方法求解数值解。

（3）边界条件、初始条件及其他参数的选择 根据流体是否可压、建立特殊的可行的问题、精度的要求、计算机的能力、时间的限制等判断依据，选择标准K-ε模型^[82]。标准K-ε模型为基于湍流动能和扩散率的半经验公式。K方程为湍流动能方程，是个精确方程；ε方程为由经验公式导出的扩散方程。K-ε模型在工程中应用最为广泛，而且也经受了普遍的检验。

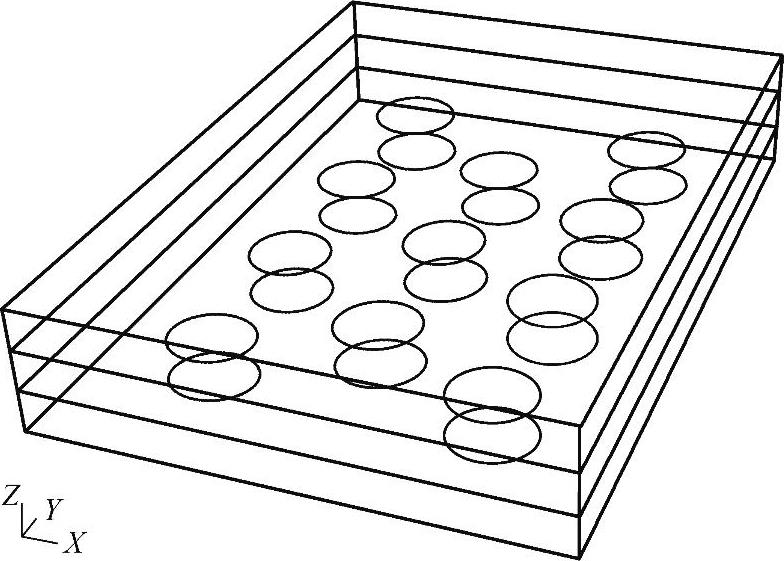
图8-3 分析对象模型

对瞬态导热过程采用非稳态的计算方法。采用时间的一阶计算精度。

壁面边界条件需要输入下列信息，即壁面温度、流体入口处温度、流体及壁面导热参数，以及壁面阻力系数。材料热物理性质见表8-1。

表8-1 材料热物理性质

入口类型的选取依据实际的物理模型而定，常见的入口类型有速度入口、压力入口和质量入口。无论哪种类型都可以通过设置其坐标方向的分量来直接给出。本书以速度入口为主要边界条件，同时辅以压力入口边界条件，以减少回流现象，提高收敛速度。涉及传热的还需给出其温度值。同时入口的湍动能k_in和湍动能耗散率ε_in也需设置，计算依据下列公式^[83]：

式中，u-为平均流速；I为完全发展的核心紊流强度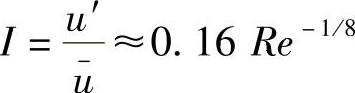，；雷诺数，u为流速，ρ为密度，μ为黏性系数，d_e为当量直径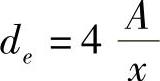，，A为入口截面面积，x为入口截面的湿周。

式中，C_μ≈0.09；k为湍动能；l为管内湍流充分发展段的湍流尺度，l=0.25d_e。

（4）支撑体形状对冷却的影响 分别采用图8-4所示的几种形状进行冷却分析，其分别为密集式肋条支撑（方案a-1）、分散式肋条支撑（方案a-2）、圆柱形支撑（方案b-1）、菱形支撑（方案b-2）、集中式复杂形状支撑（方案c-1）、分散式复杂形状支撑（方案c-2）。

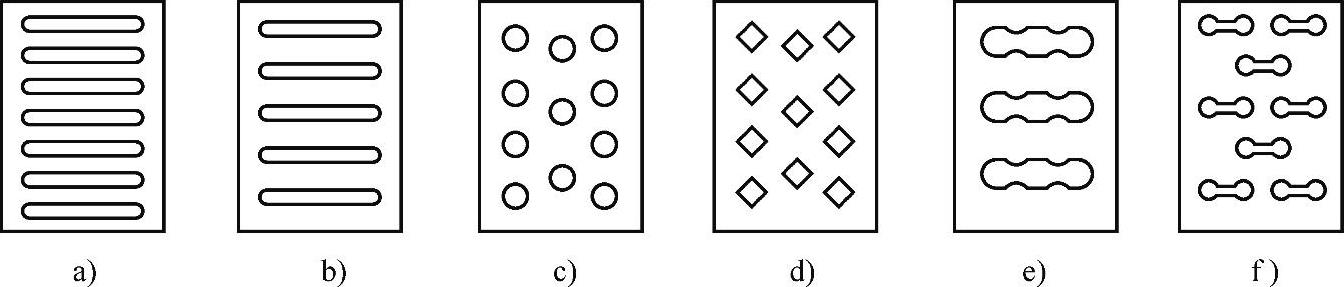
图8-4 冷却系统示意图

a）方案a-1 b）方案a-2 c）方案b-1 d）方案b-2 e）方案c-1 f）方案c-2

根据式（8-2）可得钢板从900℃降温到400℃放出热量Q=130708J。整理试验数据，见表8-2。其中q₁是单位时间上壁面换热量，q₂是单位时间支撑体壁面换热量，q_z是各方案冷却系统换热量，t是换热时间。可以看出方案b-1换热效率最高。

表8-2 六种方案单位时间换热量

(www.xing528.com)

为了研究不同支撑体对流场的作用及流场各点处换热状态，在不同位置定义断面，用以观察各支撑体头部、两端及尾部流场的变化，其中速度场和湍动能场用面积加权方法积分，温度场用质量加权方法积分。图8-5所示为方案a垂直方向中心面温度场分布图。

由图8-5可知，在直板式冷却系统中，支撑体排列越密，水流最小横截面面积越小，水速越高，即

v=V/S_水 （8-6）

S_水=S_总-S_支撑=h（L-ns） （8-7）

式中，V为单位时间内流入的冷却水体积；h为冷却水体高度；L为水体宽度；n为直板个数；s为直板宽度。

提高水速可增大冷却水雷诺数Re，同时直板个数增加，加大了换热面积，换热效率提高。因此，方案a-1的换热效果比方案a-2好。

图8-6所示为方案b垂直方向中心面温度场分布图。

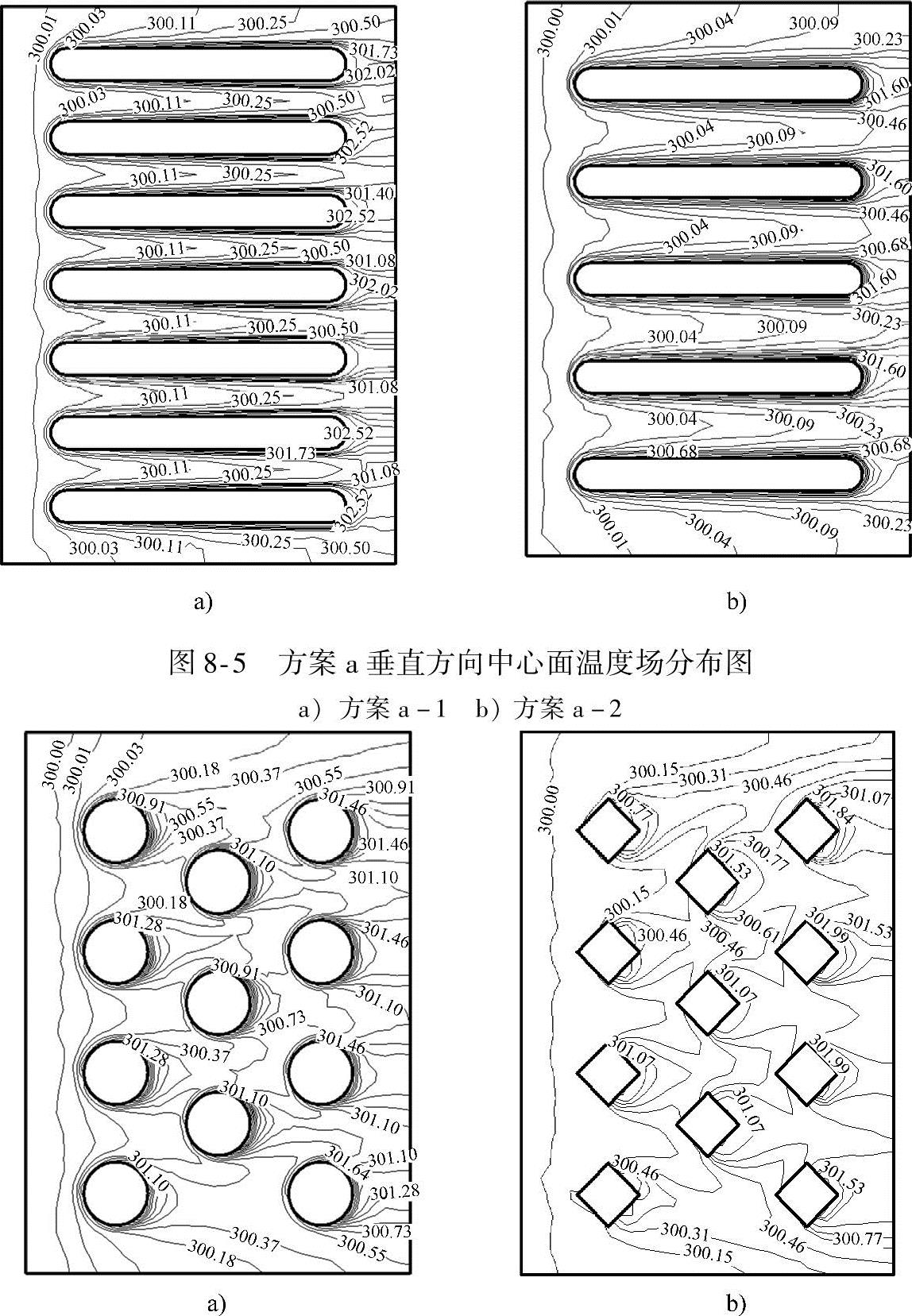
图8-6 方案b垂直方向中心面温度场分布图

a）方案b-1 b）方案b-2

由图8-6可知，在相同支撑面积的条件下，圆柱形支撑体比菱形支撑体换热面较少，但是尾部形成小块热集中区域；菱形面积大且因头部水流较为稳定，雷诺数Re较小，但在两端绕流脱体引起的回流、漩涡和涡束支撑体头处绕流脱体引起的回流、漩涡和涡束严重。综合考虑，圆柱形支撑体换热量为9803W，而菱形支撑体换热量为7023W，因此方案b-1比方案b-2换热效果好。

图8-7所示为方案c垂直方向中心面温度场分布图。

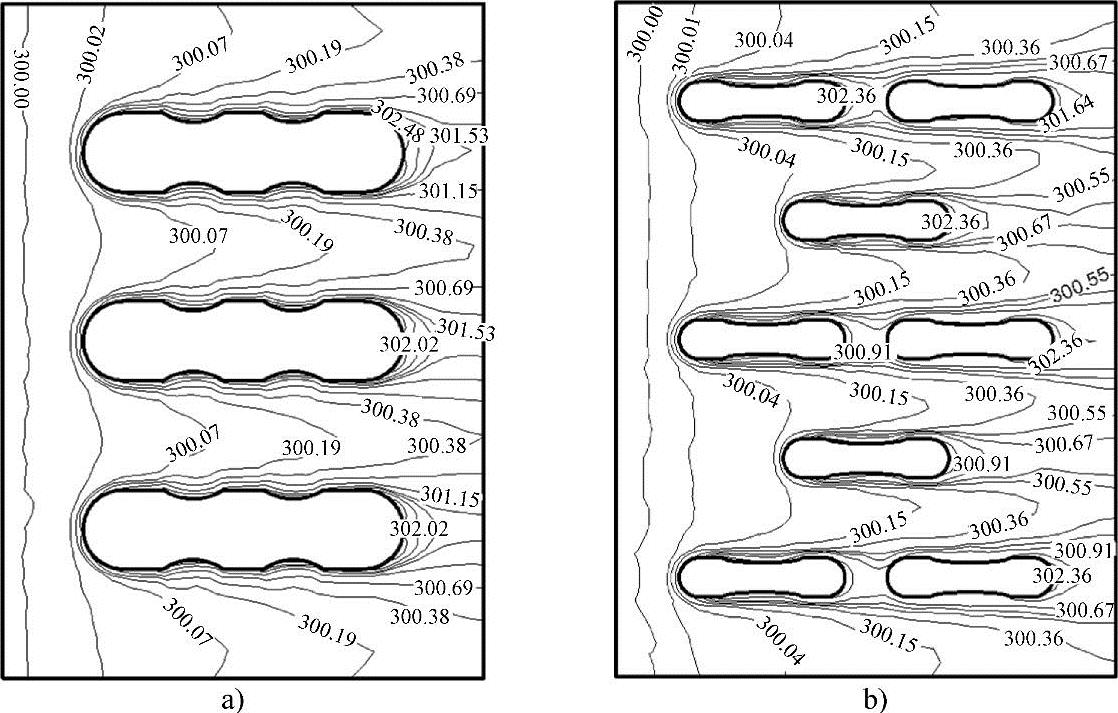
图8-7 方案c垂直方向中心面温度场分布图

a）方案c-1 b）方案c-2

由图8-7可知，方案c-2支撑体分布较为分散，两者扰流条件相当，但是方案c-1在两个水平方向支撑体之间，由于间距较小，容易造成热集中现象。综合比较，因此方案c-2比方案c-1换热效果好。

为了将六种方案综合比较，将其结果数据整理归纳。定义七个垂直于水流方向的断面，以断面位置为横坐标，断面速度、湍动能及温度为纵坐标，画出六种方案的速度标量图，湍动能图及温度图，如图8-8～图8-10所示。

图8-8 六种方案的速度标量图

图8-9 六种方案的湍动能图

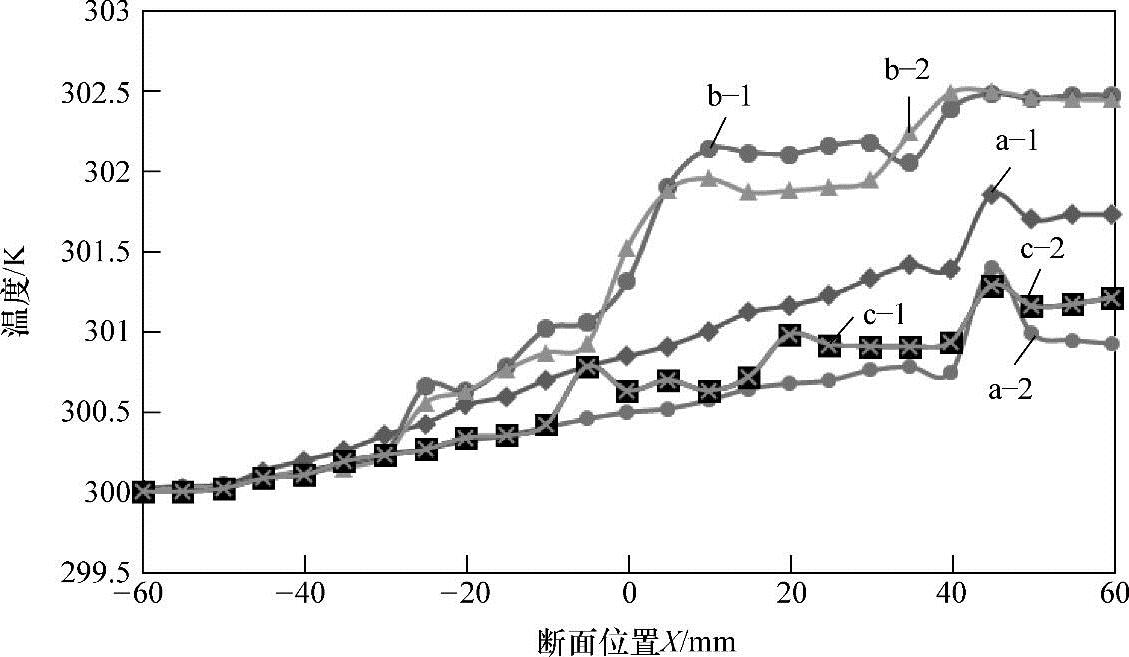
图8-10 六种方案的温度图

直板式冷却系统中，扰流件少，冷却水雷诺数Re低，换热效果差，同时在支撑体中心部分出现热集中现象；复杂形状的分散式支撑的设计初衷是增加表面粗糙度，从而增加扰动，提高换热效率。经过数值模拟，发现在凹槽处出现漩涡与回流，此处与外界换热不再是对流换热，变为单纯导热，降低了平均表面换热效率。同时根据本书分析，得出凸表面比凹表面换热好的结论^[60]。简单形状的分散式支撑，支撑体分散布置，热集中点较少，且热集中点与冷却水流经的点温差较小；布置方式及凸面的支撑体形状可以增大水流扰动，同时避免不必要的回流和漩涡，增加了换热效率。因此选择形状简单的分散式支撑。

（5）凹模厚度的影响 为了研究不同的凹模厚度对散热的影响，选取10mm、15mm、20mm及极限厚度1000mm（作为没有冷却系统的模拟），研究钢板温度随时间变化情况，如图8-11所示。

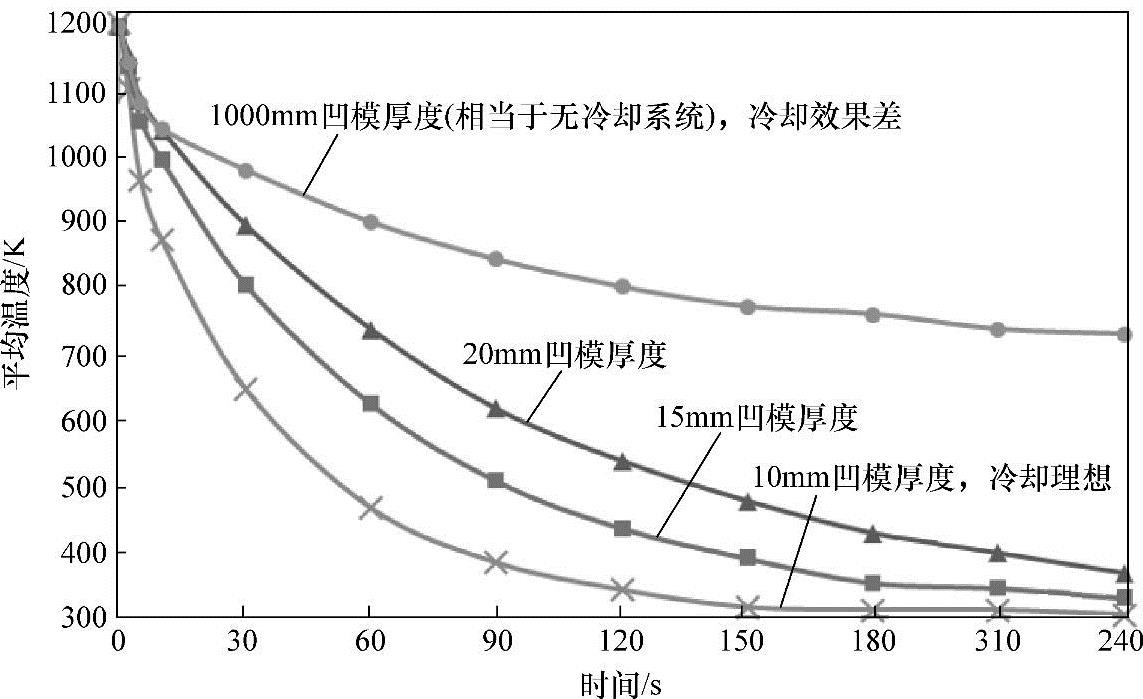
图8-11 不同凹模厚度时钢板平均温度随时间变化

其中，凹模厚度为10mm、15mm、20mm时，钢板平均温度随时间变化规律根据最小二乘法原理拟合，分别见式（8-8）～式（8-10）。

T=820.64exp（-t/34.11）+311.81 （8-8）

T=827.17exp（-t/57.08）+323.11 （8-9）

T=827.46exp（-t/82.82）+331.60 （8-10）

式中，T为温度；t为时间。

分析可知，0mm厚度凹模相当于直接淬火，冷却效果不言而喻；随着模具厚度的增加，冷却速度降低，特别是冷却加速度减小，即曲线的陡度减小。此时要求更长的保压时间及模具散热时间。对于生产率的提高不利。因此，在模具设计中，在保证凹模机械强度的前提下，尽量减小凹模厚度。

（6）水流速度的影响 水流速度是影响冷却速度的重要参数之一，模具通过与冷却水的对流换热，保持自身温度在一定范围，以确保钢板迅速冷却。同时，冷却水速度直接影响着模具在一次冲压之后恢复冲压前温度场状态的时间。

以圆柱支撑式冷却系统为例，取支撑柱直径为10mm，选择水流速度分别为0.01m/s、0.1m/s、1m/s、10m/s、20m/s、30m/s，模拟结果如图8-12所示。

因此，水流速度越高，冷却效果越好。值得注意的是：水流速度过高后，水流速度对钢板冷却时间影响不大（10m/s、20m/s、30m/s水流速度相比，钢板温度随时间变化情况基本相同）；水流速度过低（0.01m/s）却无法达到要求的冷却速度。

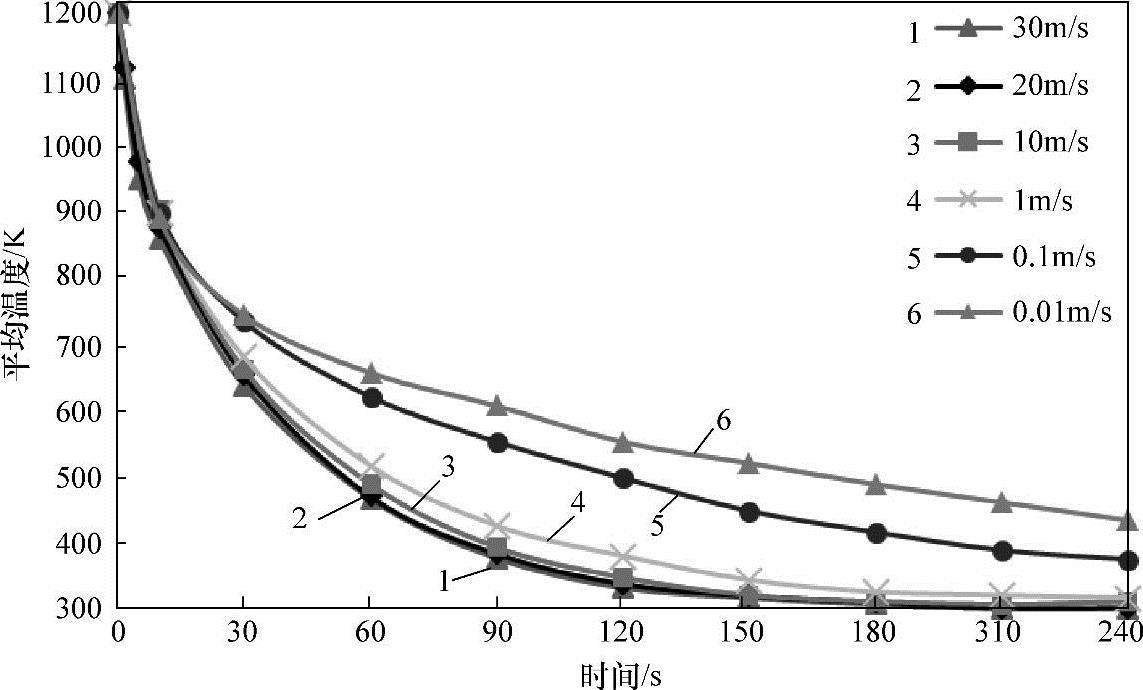
图8-12 不同水流速度对冷却效果的影响